不等式约束的优化问题

一般形式

约束部分

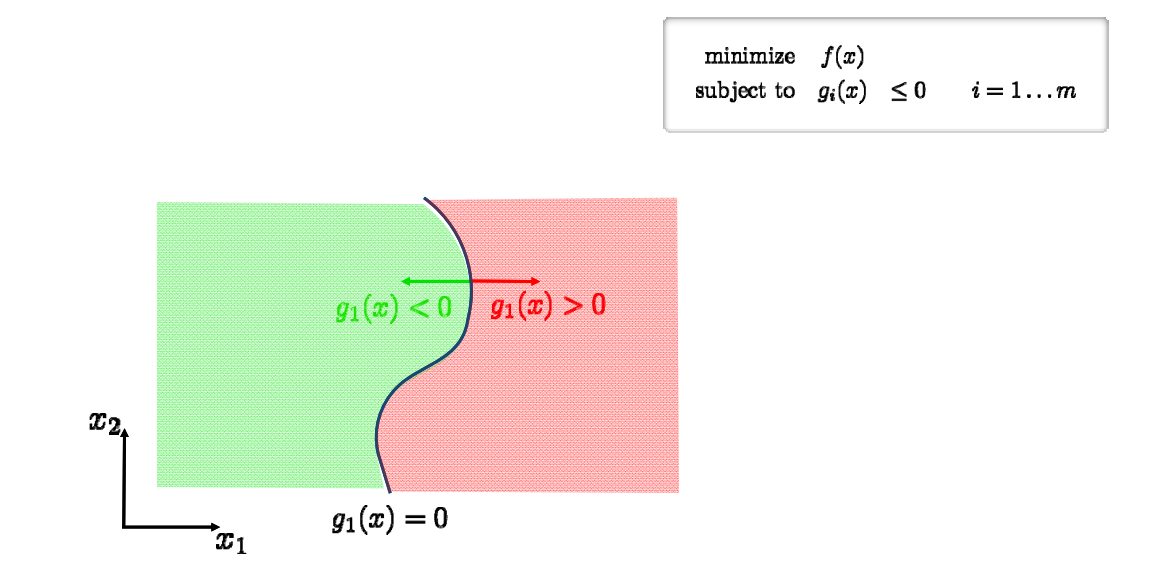
[1:20:17] 把流形空间分成了两部分，绿色空间为可行域 feasible domain

优化部分

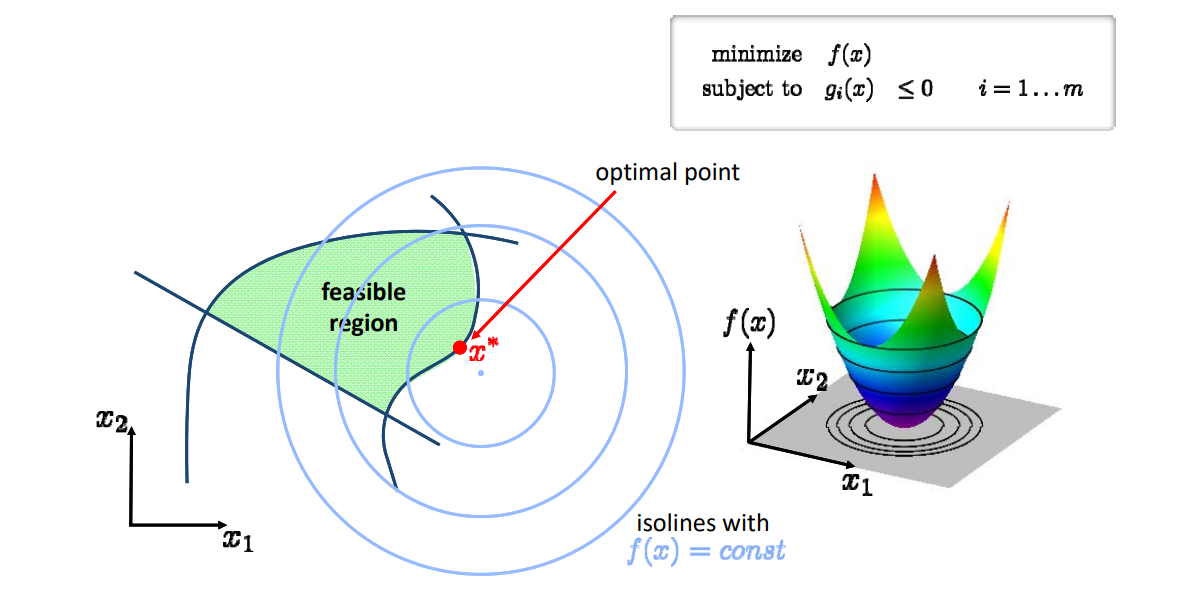
解优化方法

1. 把问题转化为Langrangian形式:

$$L(x,\lambda )=f(x)+\sum_{i=1}^{m} \lambda _ig_i(x)$$

2. f(x)的约束为Karush‐Kuhn‐Tucker (KKT)

• Stationarity: $\nabla f(x^\ast )+\sum_{i=1}^{m} \lambda _i\nabla g_i(x^\ast )=0$

• Primal feasibility: $g_i(x^*)\le 0$

• Dual feasibility: $\lambda _i\ge 0$

• Complementary slackness: $\lambda _ig_i(x^*)= 0$

3. 具体求解过程，没有展开

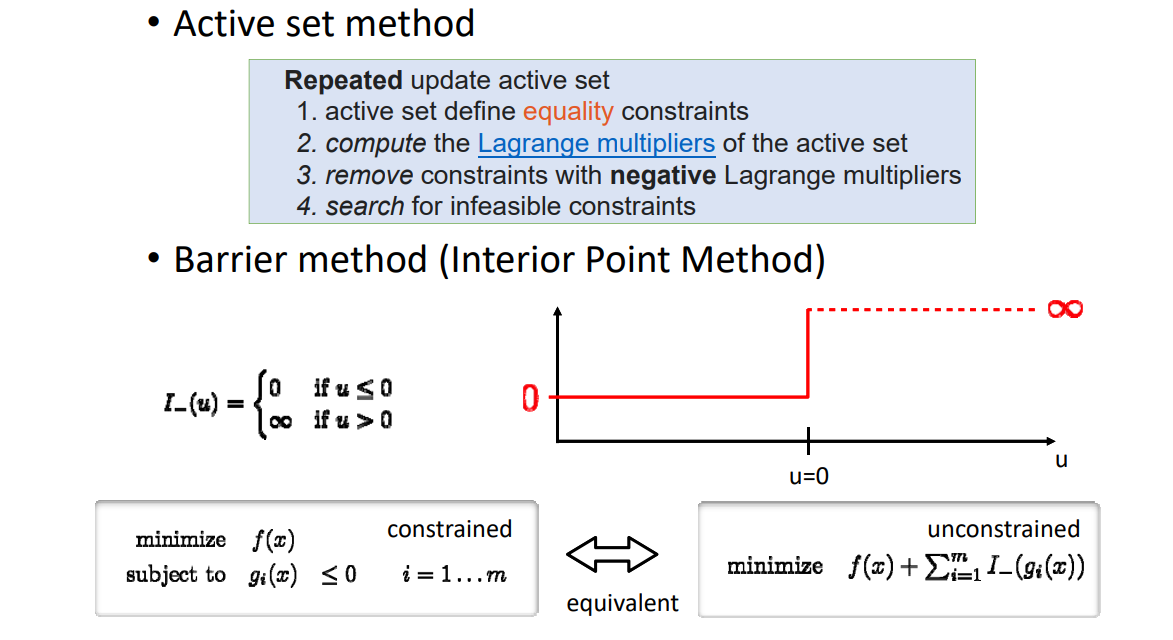
[1:23:29] Active set,积极集。
Interior Point.内点法。

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/