多项式插值定理
🔎 [16:46]
定理:若\(x_i\)两两不同,则对任意给定的\(y_i\),存在唯一的次数至多是\(n\)次的多项式\(p_n\),使得\(p_n(x)=y_i,i=0,\cdots,x^n\)。
✅ 唯一的多项式p的意思是唯一的一组系数\(a_0, \cdots, a_n\)
证明:在幂基\((1,x,\cdots,x^n)\)下待定多项式\(p\)的形式为:
$$
p(x)=a_0+a_1x+a_2x^2+\cdots+a_nx^n
$$
定理不限于幂基,下面证时过程只是以幂基为例
由插值条件\(p(x_i)=y_i,i=0,\cdots,n\)得到如下方程组:
👆 如果基函数选取不一样,方程组的系数矩阵不同
系数矩阵为Vandermonde矩阵,其行列式非零,因此方程组有唯一解。
✅ 如果不使用幂基而是别的基函数,也能得到上述方程组并解出唯一解,只是矩阵的内容不同。
要求解的系数是\(a_1,a_2, \cdots, a_n\),此处系数a是未知数,而不是通常理解的\(x\), \(x\) 代表输入,因此是已知量。
技巧1:构造插值问题的通用解
🔎 [17:44] ✅ 上一页方法中的问题:每次x或y变化都要构造一个公式来解。本页的目的是,只变y而x不变时不需要构造矩阵和解方程。
给定 \(n+1\)个点 {\((x_0,y_0),\cdots,(x_n,y_n)\)}, 寻找一组次数为\(n\)的多项式基函数\(l_i\)使得
$$ l_i(x_j) = \begin{cases} 1, & \text{ if } i=j \\ 0, & \text{ if } i\neq j \end{cases} $$
那么,插值问题的解为:
$$
P(x)=y_{0} l_{0}(x)+y_{1} l_{1}(x)+\cdots+y_{n} l_{n}(x)=\sum_{i=0}^{n} y_{i} l_{i}(x)
$$
✅ 这样做的好处是,即使y变化,也不用重新解方程组。\(l_i(x)\)可以通过上述方程组提前解出来,以\(y\)为系数对\(l_i(x)\)做线性组合,就可以得到\(P(x)\)
多项式\(l_i(x)\)被称为拉格朗日多项式,即拉格朗日插值问题的通用解。
该方法称为拉格朗日插值。
给定\(n+1\)个点,通过上面的方法解方程组,可以解出\(l_i(x)\)系数,从而得到拟合函数。
但 \(n+1\) 个点有任何一点改变,都要重新"构造方程组→解系数→得拟合函数"。
该技巧对以上过程做简化。在 \(n+1\) 个定点的\(x\)不变而只有\(y\)的变化的情况下,无须解方程而快速得到拟合函数。
具体步骤为:
2.先求拟合函数 \(l_i(x)\). 用上一页的方法。
构造用于拟合\(l_i(x)\)的数据点。其中\(x_i\)为原给定的\(n+1\)个时,\(x_i\),\(y_i\)为公式(1)中的\(l_i(x_j)\),这样给每个\(l_i(x)\)构造了\(n+1\)个用于拟合点。例如:
\(n+1\)个点{\((x_0,1),(x_1,0)\dots ,(x_n,0)\)}导拟合函数\(l_0(x)\)
这样就得到了\(n+1\)个函数\(l_i(x)\)
在拟合\(l_i(x)\)的过程中只用到了原给定数据点的\(x\)而没有用 \(y\)。因此,只要x不变,\(l_i(x)\)函数就一直适用。
要拟合的函数\(P(x)\)就成了\(l_i(x)\)的线性组合,\(y_i\)是系数。
💡 我的思考:
根据 \(Aa=y\) 解出\(a\),得到拟合函数\(f(x)= A(x)\cdot a\)
现在,先算出 \(A{a}' = E,根据Ey=y可知:A{a}'y=Aa\).
因此得到拟合函数\(f(x)=A(x)a=A(x){a}' y\).
结论:把计算的过程或目标分解,分析每一部分计算的依赖项。根据依赖项决定是否能提前算好。
怎么计算多项式\(l_i(x)\)?
\(n\)阶多项式,且有以下\(n\)个根
$$ x_0,x_1,x_2,\cdots,x_{i-1} ,x_{i+1} ,\cdots,x_n $$
故可表示为
$$
l_i(x) \\
=C_{i}\left(x-x_{0}\right)\left(x-x_{1}\right) \ldots\left(x-x_{i-1}\right)\left(x-x_{i+1}\right) \ldots\left(x-x_{n}\right) \\
=C_{i} \prod_{j \neq i}\left(x-x_{j}\right)
$$
由\(l_i(x_i)=1\)可得
$$
1=c_{i} \prod_{j \neq i}\left(x_{i}-x_{j}\right) \Rightarrow c_{i}=\frac{1}{\prod_{j \neq i}\left(x_{i}-x_{j}\right)}
$$
最终多项式基函数为
$$
l_{i}(x)=\frac{\prod_{j \neq i}\left(x-x_{j}\right)}{\prod_{j \neq i}\left(x_{i}-x_{j}\right)}
$$
多项式\(l_i(x)\)被称为拉格朗日多项式
技巧2:更方便的求解表达
Newton插值:具有相同“导数”(差商)的多项式构造(\(n\)阶Taylor展开)
定义:
一阶差商:
$$
f\left[x_{0}, x_{1}\right]=\frac{f\left(x_{1}\right)-f\left(x_{0}\right)}{x_{1}-x_{0}}
$$
\(k\)阶差商:
设{\(x_0,x_1,\cdots,x_k\)}互不相同,\(f(x)\)关于{\(x_0,x_1,\cdots,x_k\)}的\(k\)阶差商为:
$$
f\left[x_{0}, x_{1}, \cdots, x_{k}\right]=\frac{f\left[x_{1}, \cdots, x_{k}\right]-f\left[x_{0}, x_{1}, \cdots, x_{k-1}\right]}{x_{k}-x_{0}}
$$
所以Newton插值多项式表示为: $$ N_{n}(x)=f\left(x_{0}\right)+f\left[x_{0}, x_{1}\right]\left(x-x_{0}\right)+\cdots+f\left[x_{0}, x_{1}, \cdots, x_{n}\right]\left(x-x_{0}\right) \cdots\left(x-x_{n-1}\right) $$
🔎 [19:23]
❓ 这里也没听懂?意思是预算出的有阶的差商?
多项式插值存在的问题
系统矩阵稠密
例如Vandermonde矩阵,处处非零元素
✅ 稀疏矩阵的优势:有好的迭代方法,计算很快.
eigen库:非常有名的数学库
病态问题
依赖于基函数选取,矩阵可能病态,导致难于求解(求逆)
病态矩阵示例
考虑二元方程组,解为\((1,1)\)
$$
x_{1}+0.5 x_{2}=1.5
$$
$$ 0.667 x_{1}+0.333 x_{2}=1 $$
对第二个方程右边项扰动0.001,解为 (0,3)
$$
x_{1}+0.5 x_{2}=1.5
$$
$$ 0.667 x_{1}+0.333 x_{2}=0.999 $$
对矩阵系数进行扰动,解为(2,-1)
$$
x_{1}+0.5 x_{2}=1.5
$$
$$ 0.667 x_{1}+0.334 x_{2}=1 $$
✅ 对系数矩阵或\(y\)向量做微小的扰动,其解的变化会非常大。
输入数据的细微变化导致输出(解)的剧烈变化
将线性方程看成直线(超平面),当系统病态时,直线变为近似平行,求解(即直线求交)变得困难、不精确
矩阵条件数
$$ \kappa_{2}(A)=\frac{\max _{x \neq 0} \frac{|A x|}{|x|}}{\min _{x \neq 0} \frac{|A x|}{|x|}} $$
矩阵条件数等于矩阵最大特征值和最小特征值之间比例,条件数大意味着基元之间有太多相关性,造成不稳定。
范德蒙矩阵的条件数
多项式插值问题是病态的,因为对于等距分布的数据点\(x_i\),范德蒙矩阵的条件数随着数据点数\(n\)呈指数级增长(多项式的最高次数为\(n-1\))
✅ 多项式插值如果使用了高阶的基函数,就容易出现病态问题
因为幂(单项式)函数基的特点是,幂函数之间差别随着次数增加而减小,不同幂函数之间唯一差别为增长速度(\(x^i\)比 \(x^{i-1}\)增长快)
🔎 [26:31]
✅ 幂函数基,高阶后函数变化非常快,那么结果就会被幂底严重挠动
解决方法
好的基函数一般需要系数交替,且互相抵消问题,例如:
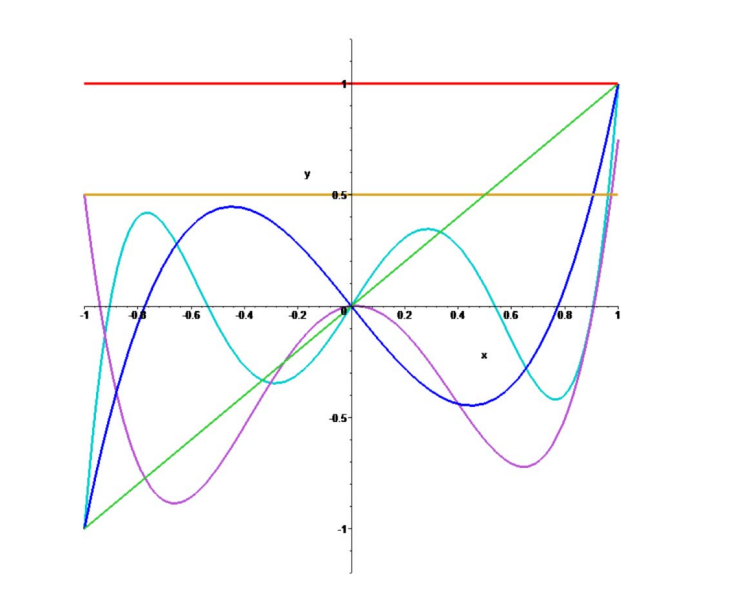
基之间互相抵消,函数就不会一直增长。
[?] 秦九韶算法
可使用正交多项式基。可通过Gram‐Schmidt正交化获得正交多项式基。
振荡(Runge)现象
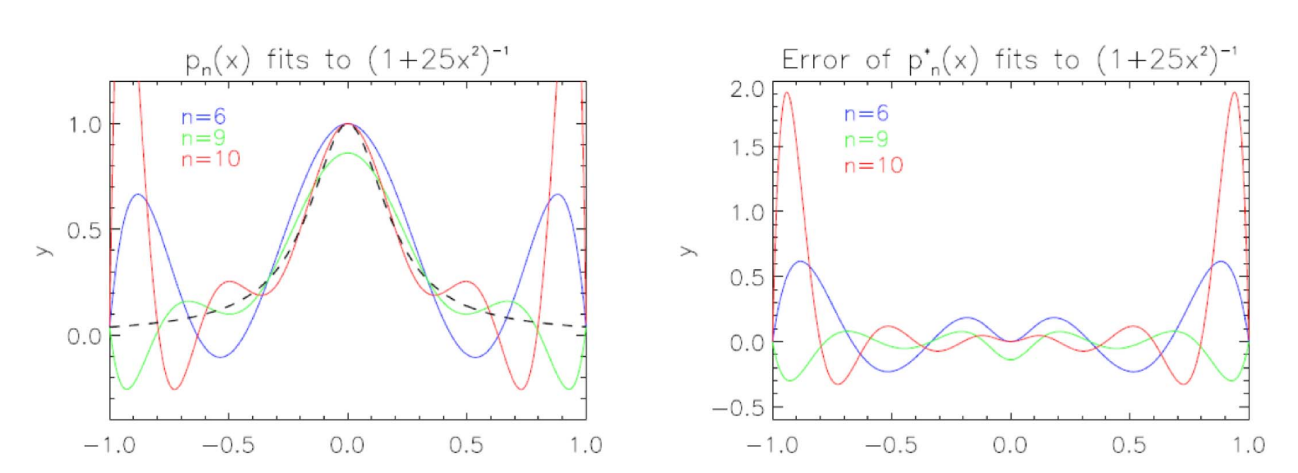
结论
多项式插值存在以下问题:
- 多项式插值不稳定,控制点的微小变化可导致完全不同的结果
- 振荡(Runge)现象,多项式随着插值点数(可以是细微)增加而摆动
因此需要更好的基函数来做插值,例如Bernstein基函数、分片多项式
本文出自CaterpillarStudyGroup,转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/