等式约束的优化问题

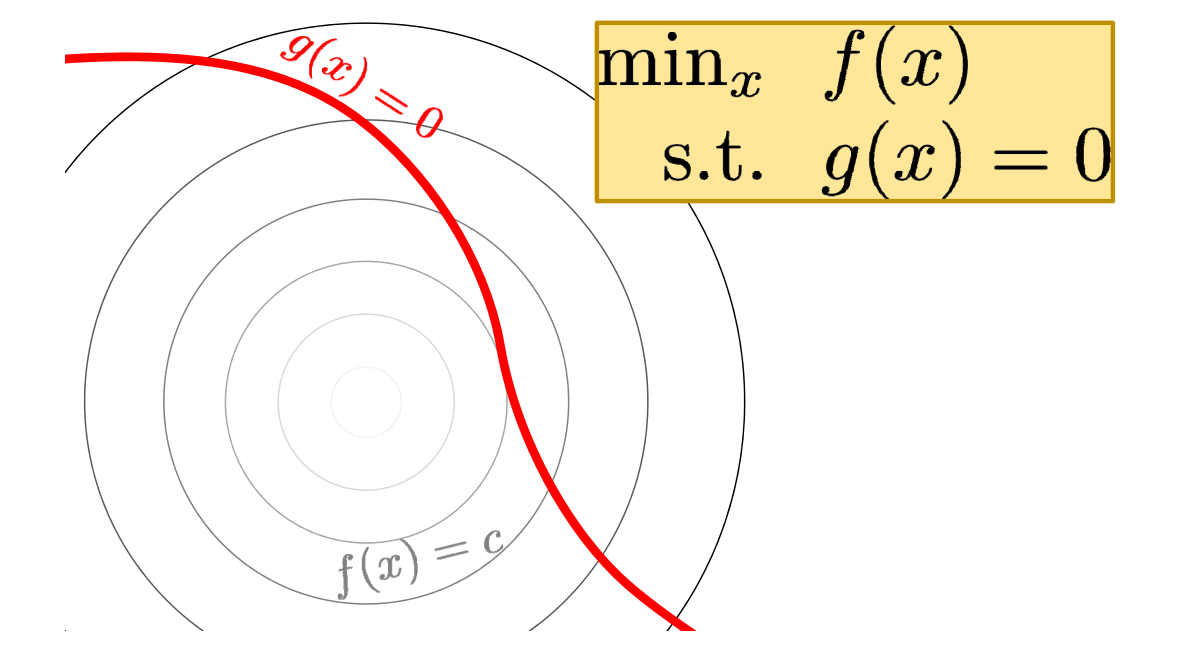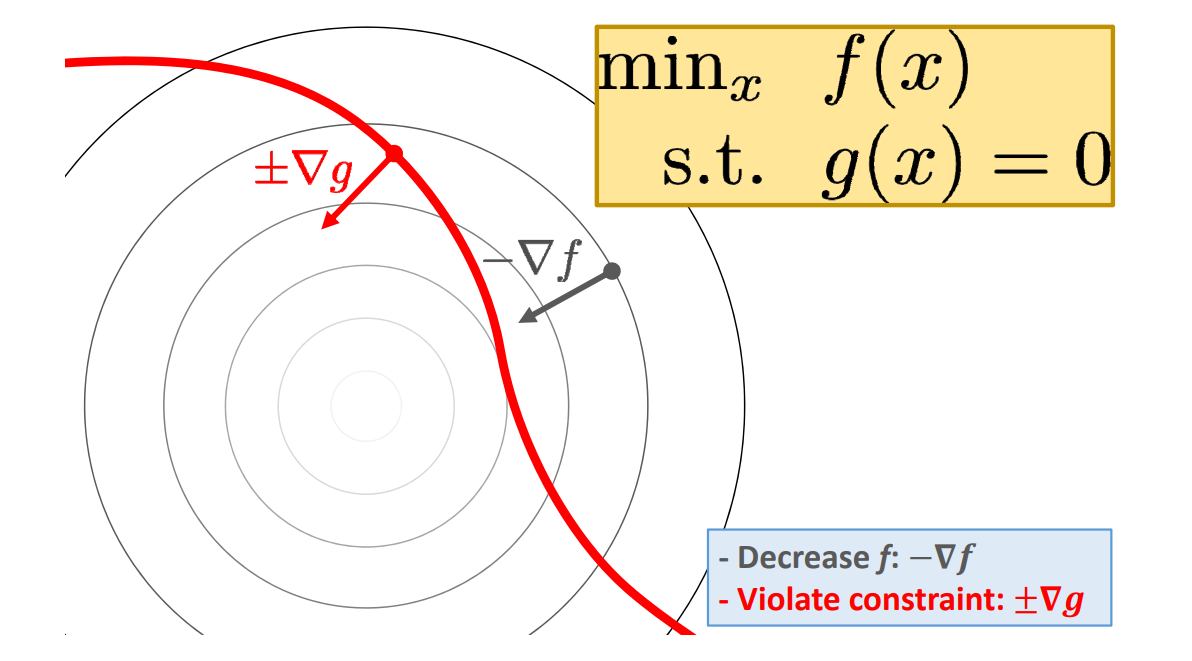$g(x)$ 是红线， $f(x)$ 由等值线构成的曲面。满足约束的极小值点具有以下特点：

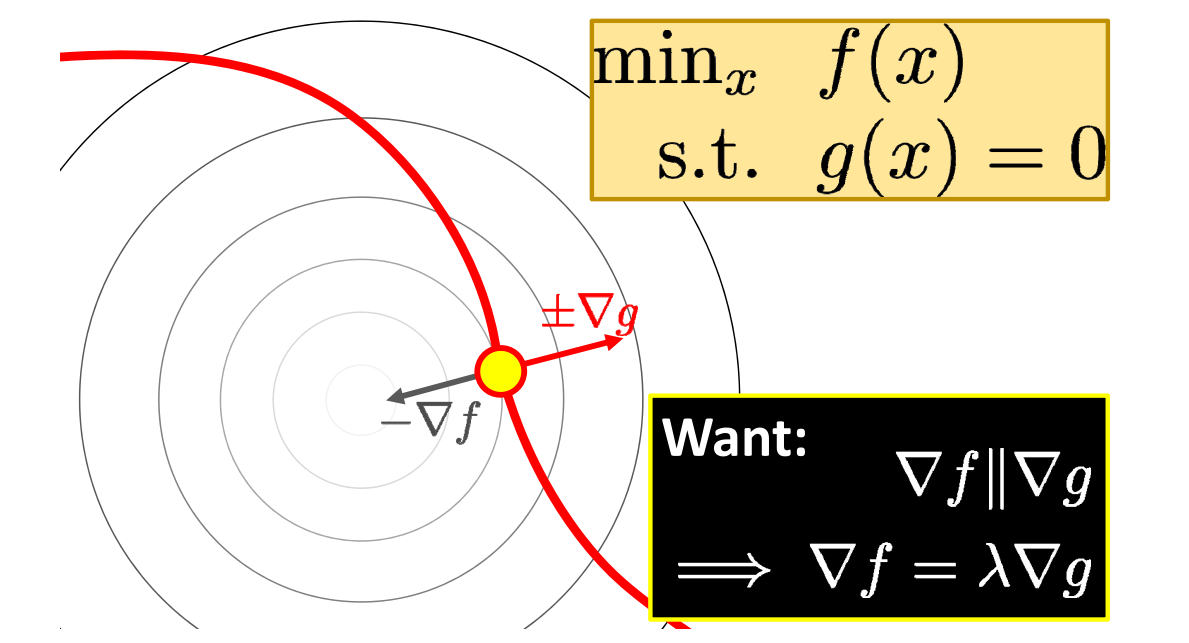
$f(x)$ 与 $g(x)$ 在该点上梯度方向重合，可能同向或反向。

[1:13:26]等值约束的优化问题转化为解方程组问题

$\begin{array}{l} \nabla \mathbf{f}(x) =\lambda \nabla g(x) \\ \mathbf{g}(x) = 0 \ \end{array}$

Many Options

• Reparameterization
Eliminate constraints to reduce to unconstrained case

• Newton’s method
Approximation: quadratic function with linear constraint

• Penalty method
Augment objective with barrier term, e.g. $f(x)+\rho |g(x)|$

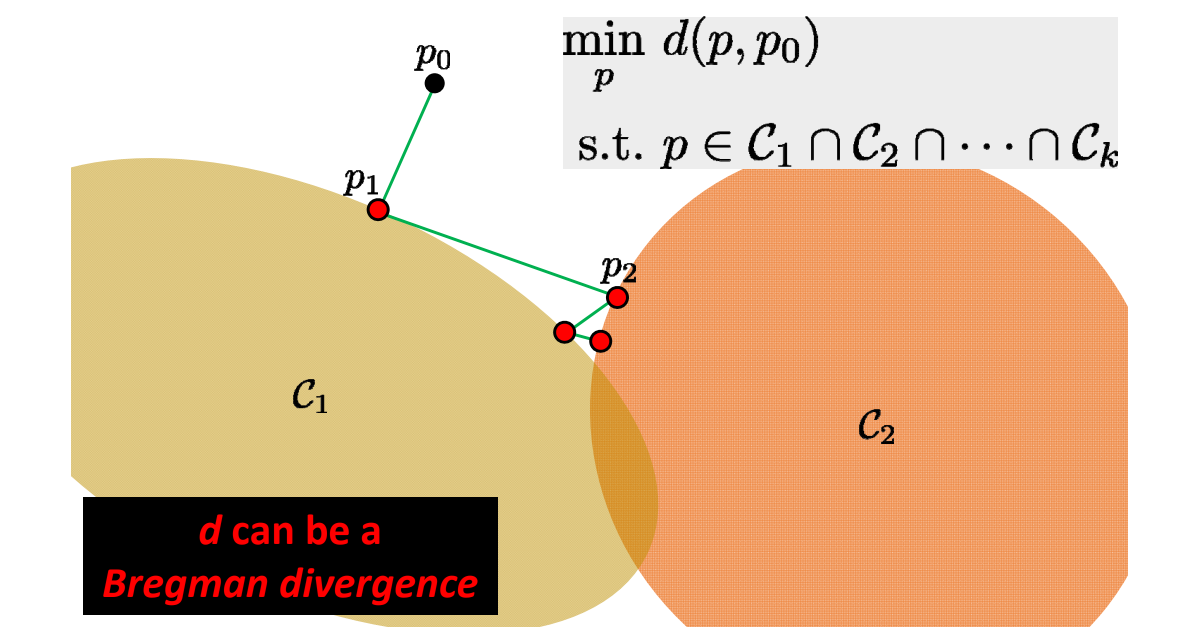
[1:14:18] $C_1,C_2,C_3$ 的代表不同的等式约束。相当于坐标法推广

[1:15:18] 把 Constrain 作为目标函数，极小划权 $\rho$ 在优化过程中会改变

[1:15:50] ADMM.把变量分离。把问题分成若干小问题分解为：小规模局部优化问题、闭式解全局优化问题。

$\begin{array}{l} \min_{x,z}& f(x)+g(z) \\ s.t. &Ax+Bz=c \\ \end{array}$

$\wedge _\rho (x,z;\lambda )=f(x)+g(z)+\lambda ^\top (Ax+Bz-c)+\frac{\rho }{2}||Ax+Bz-c||_2^2$

The Art of ADMM “Splitting”

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/