曲线的微分几何

Point p

Point p on the curve at \(u_0\)

$$ p = C (u_0)
$$

单参数曲线，因此只有一个参数\(u_0\)

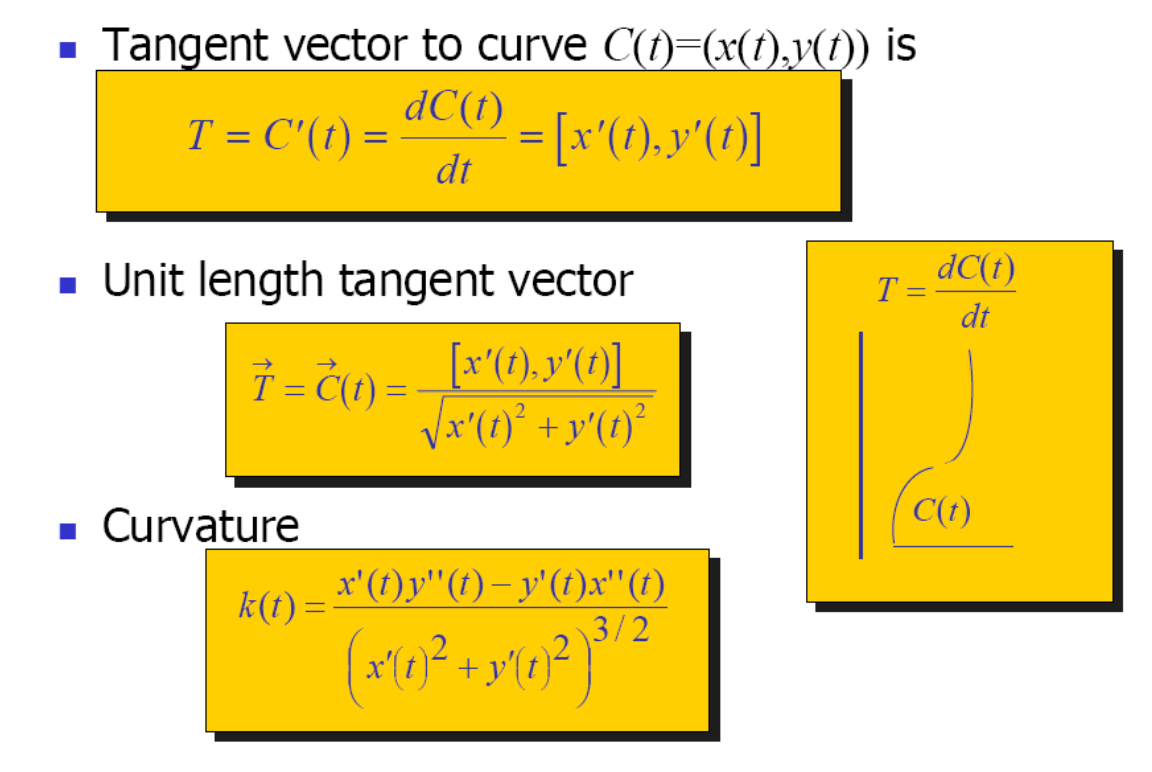
Tangent T

Tangent T to the curve at \(u_0\)

$$ C_u=\frac{\partial C(u)}{\partial u} \\ T=\frac{C_u}{||C_u||} $$

Normal N and Binormal B

Normal N and Binormal B to the curve at \(u_0\)

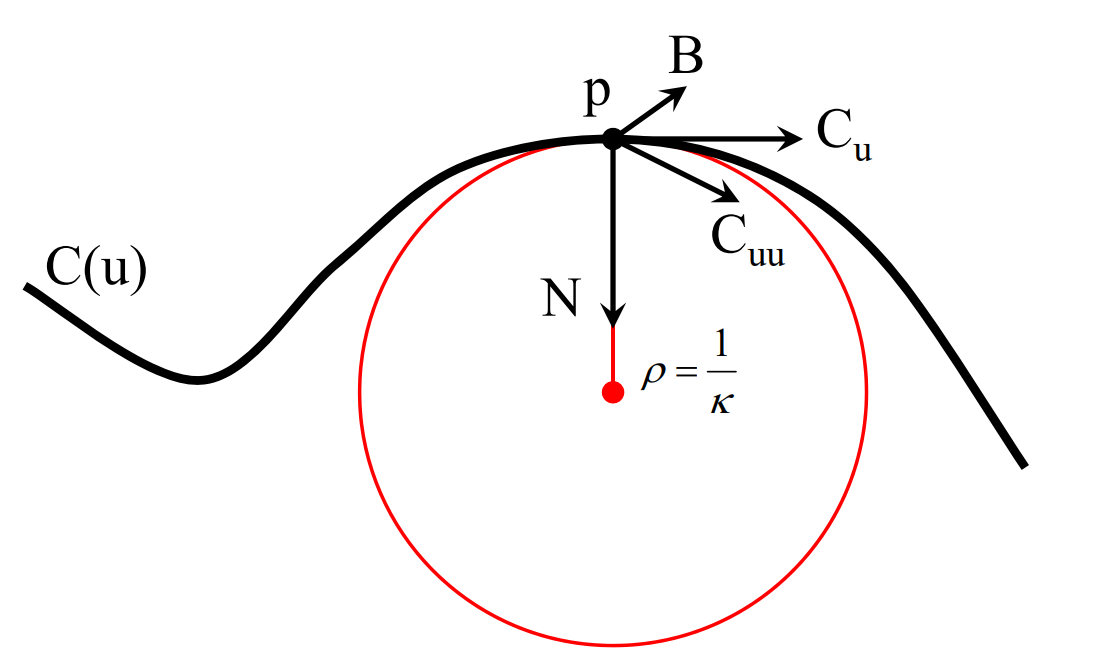
\(C_u\) 与曲线相切，又记为T
\(C_{uu} 与 N 同朝向(夹角<90^{\circ})\)
\(C_u\)和\(C_{uu}\)做叉积，得到方向B。
B 称为从法矢，B与 \(C_u\) 叉乘得到 N.
\(N,C_{uu},C_u\) 应该在同一平面内，且\(C_{uu}位于C_u 和 N \)之间。
T（切线），B(以法），N（法线）构成直角坐标系。

Curvature κ

Curvature is independent of parameterization，用于Measure curve bending

$$ k=1/R $$

其中R为二阶密切圆的半径

以上符号的关系

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/