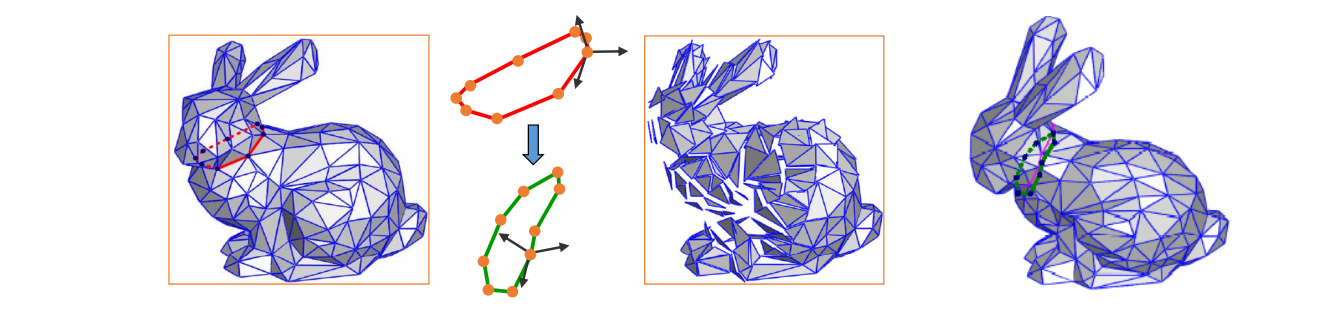
Point based editing要解决的问题

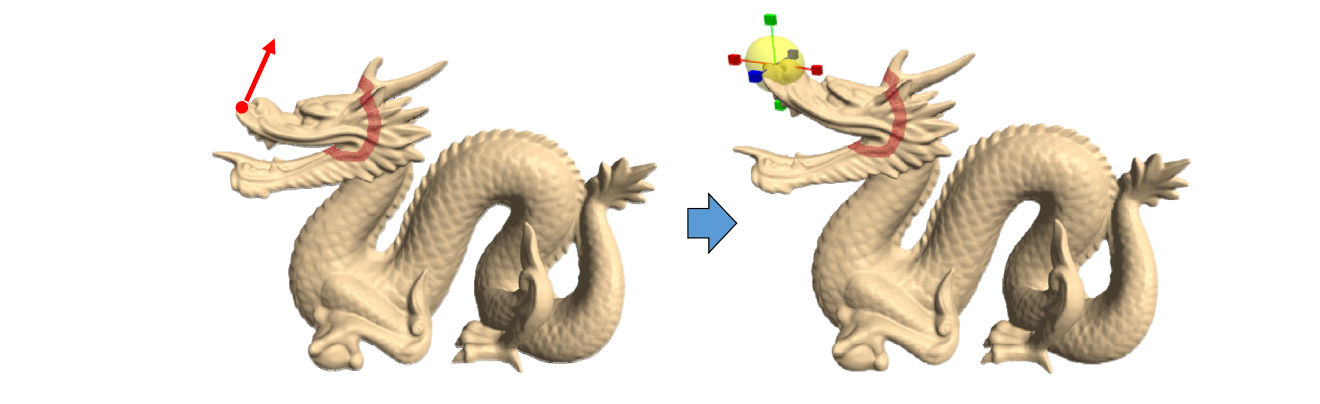
Fix 红圈上的点，Drag one or more vertices，更新红圈内的点

本质数学问题：数据插值问题，同时让f满足光滑、性质保持等约束。

$$ \begin{array}{l} \min E (f) \\ s.t. &f(x_i)=y_i,i=1,2,\dots , n \\ \end{array} $$

（1） RBF‐based Editing

（2） Moving Least Squares Method

[Siggraph 2006]

（3） Vector Field Based Deformations

[Siggraph 2006]

原理

在空间定义了一个连续的场，物理在场里面流动产生新的变化

Basic model: Moving vertex along the deformation orbit – defined by the path lines of a vector field v.

Given a time‐dependent vector field V(X,t), a Path Line X(t) in space is an integral.

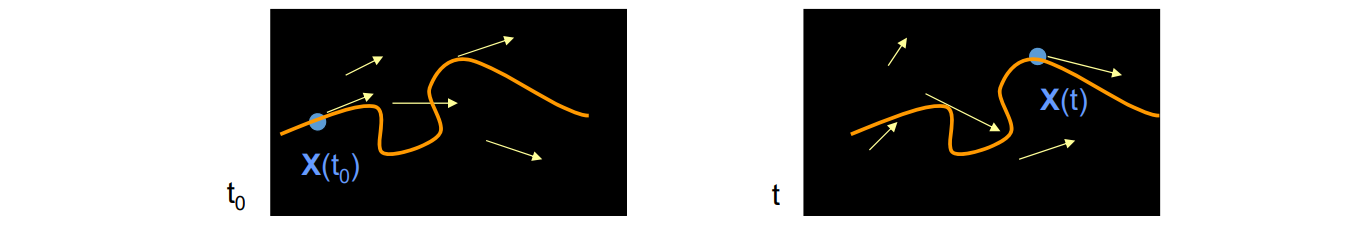
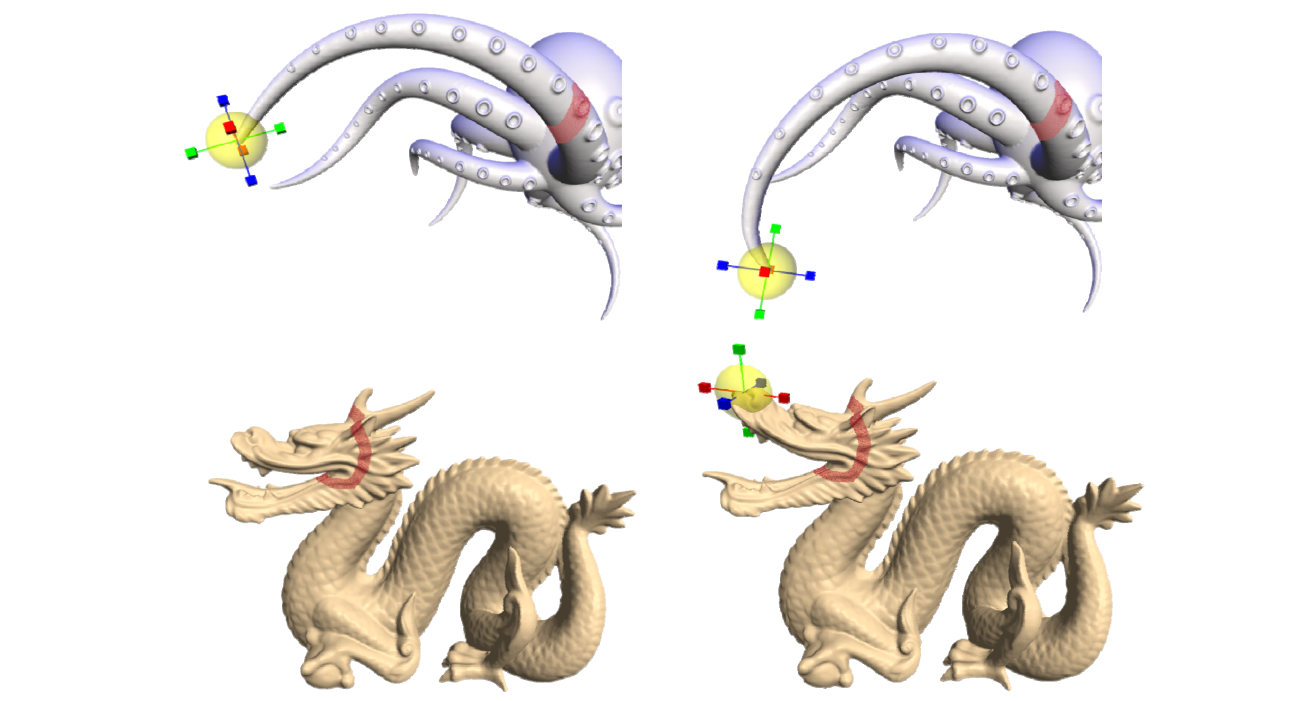
Vector Field Selection：

• Deformation Request:
  • No self‐intersection
  • Volume‐preserving
  • Details‐preserving
  • Smoothness of shape in deformation
• Divergence‐free Vector Field: \(V=(V_1, V_2, V_3)\)

$$ div V=\frac{\partial V_1}{\partial x} +\frac{\partial V_2}{\partial y}+\frac{\partial V_3}{\partial z}=0 $$

[38:39]优点:物体不会产生自交

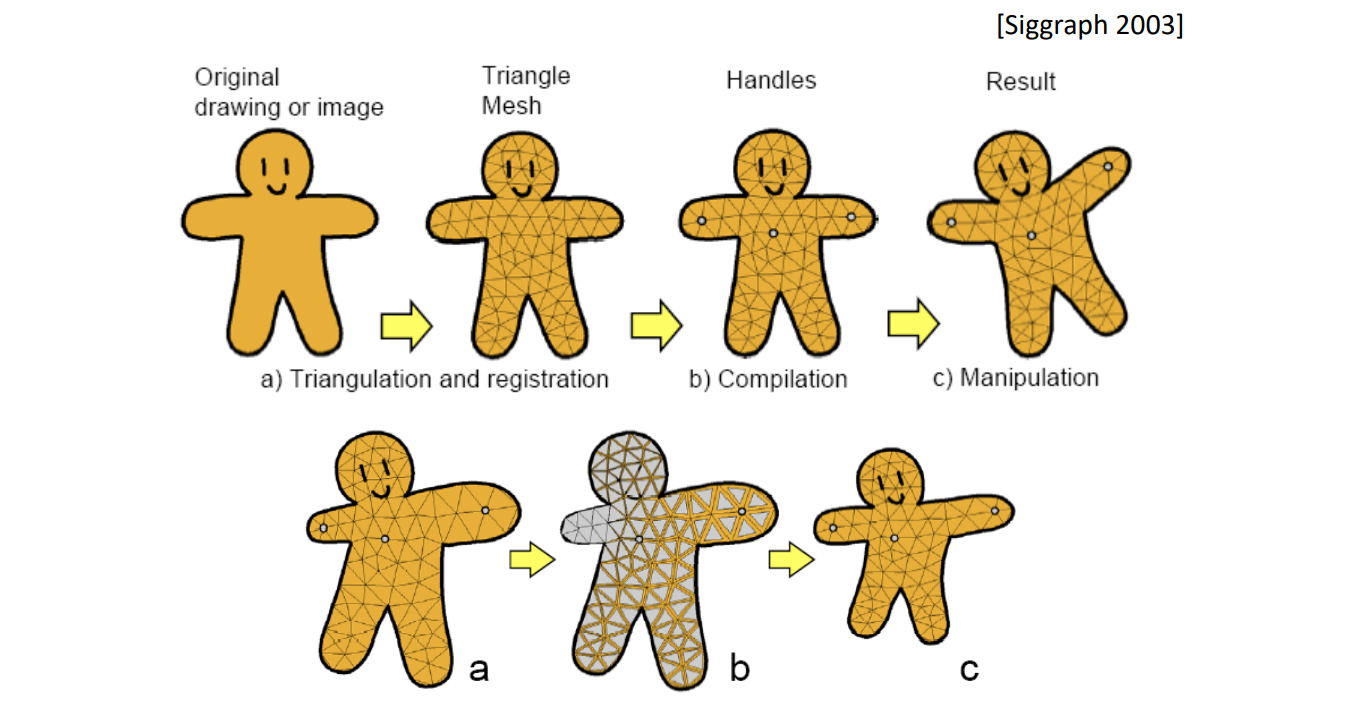
（4） Laplacian Editing [Sorkine et al. SGP 2004]

优点：
• Laplacian能体现局部细节，因此Laplacian 尽量不变可保证局部细节
• Representation with sparse matrices
• Efficient linear surface reconstruction

$$ \nu _i=\sum _{j\in N(i)}w_j\nu _j+\delta _i $$

优化目标

• Laplacian Approximation

$$ \tilde{X} =\underset{X}{argmin} \left ( ||LX-\delta ^{(x)}||^2+\sum _{j\in C}\omega ^2||x_j-c_j||^2 \right ) $$

第一项：局部细节不变，第二项：满足用户要求

• Gradient Approximation

$$ \min_\phi \iint _\Omega ||\nabla \phi -W||^2dA, $$

求解线性方程组

$$ LX=\delta\\ x_j=c_j, \quad j\in\left \{ j_1,j_2,\dots,j_k \right \} $$

Results

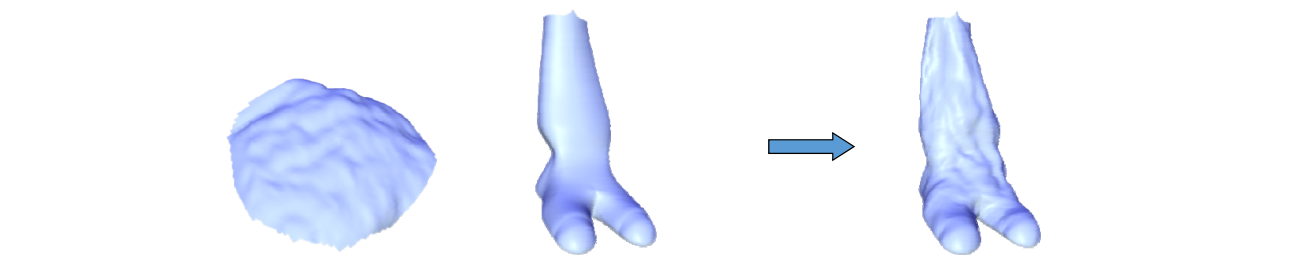
Detail transfer and mixing

这是基于Laplace的point based的一个应用

[40:45] 把一个 mesh 的 Laplacian 细节迁移到另一个 mesh上

要求网格一一对应

方法：Mixing Laplacians，即Taking weighted average of \(\delta _i\) and \(\delta '_i\)

Mesh transplanting

这是基于Laplace的point based的一个应用
[41:29] 把一个模型拼接到另一个模型上

可能用[0,1]控制Laplace的混合比例，造成渐变效果。

Invariance – solutions

• Explicit transformation of the differential coordinates prior to surface reconstruction
  • Lipman, Sorkine, Cohen‐Or, Levin, Rössl and Seidel [SMI 04], “Differential Coordinates for Interactive Mesh Editing”,
    • Estimation of rotations from naive reconstruction
• Yu, Zhou, Xu, Shi, Bao, Guo and Shum [SIGGRAPH 04], “Mesh Editing With Poisson‐Based Gradient Field Manipulation”,
  • Propagation of handle transformation to the rest of the ROI using geodesic distances
• Zayer, Rössl, Karni and Seidel [EG 05], “Harmonic Guidance for Surface Deformation”,
  • Propagation of handle transformation to the rest of the ROI using harmonic functions

（5） Poisson Mesh Editing

Yu et al. Mesh Editing With Poisson-Based Gradient Field Manipulation. Siggraph 2004.

这个方法起源于一种图片算法，把图像一部分融合到另外一个图像.让边界无缝融合，用目标的颜色结合源的梯度。
把这个方法用到3D图形上，源的梯度就演变为源的Laplace。

• The representation: the gradients of the functions X, Y, Z on each triangle of the mesh
• Deformation: propagate the transformation of the handle onto the ROI using geodesic distances

• Inspiration: Poisson Image Editing [Pérez et al. 03]

• Reconstruct a function from its gradients via the Poisson equation:

$$ \underset{f}{\arg \min } \underset{\Omega}{\int}||\nabla f-\mathbf{w}||^{2}, \quad s.t. \quad f\left |_{\partial \Omega }= f^* \right | _{\partial \Omega} $$

$$ \Downarrow $$

$$ \Delta f=\operatorname{div} \mathbf{w} \quad with \left.\quad f \right|_{\partial \Omega}=\left.f^{*}\right| _{\partial \Omega} $$

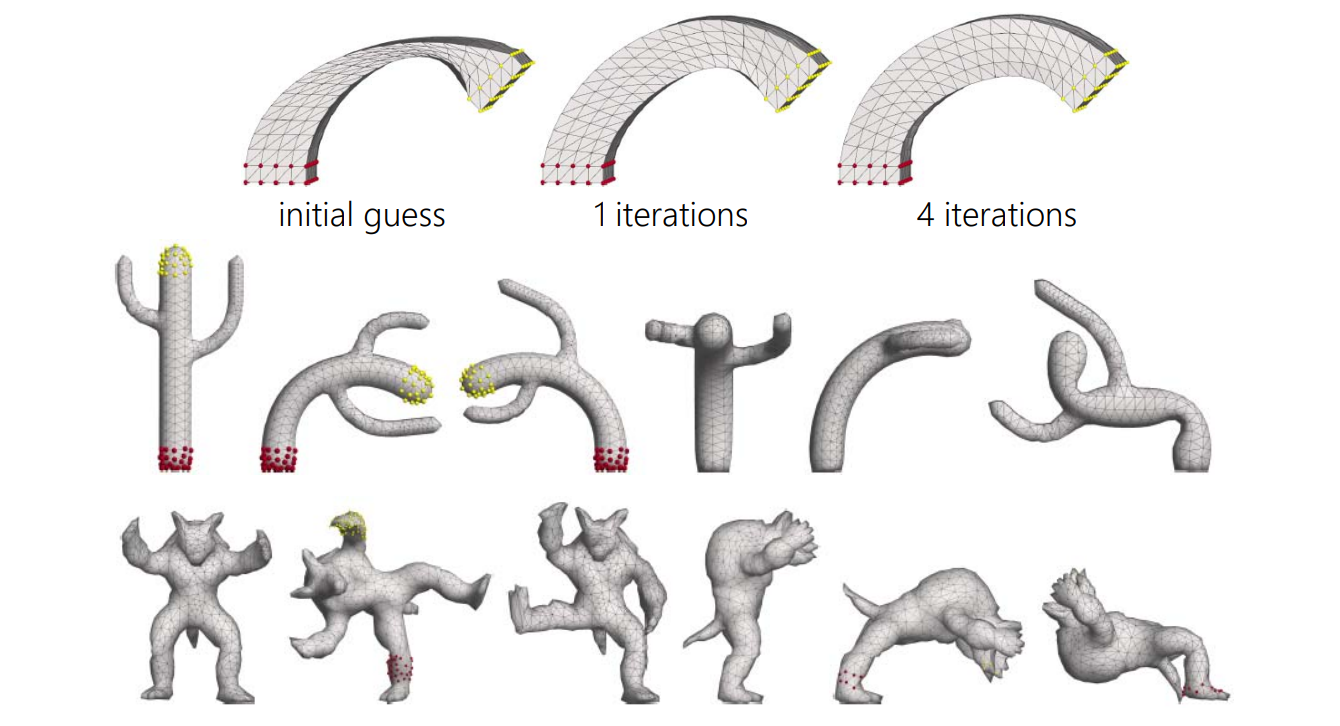
（6）（7） As‐rigid‐as‐possible Deformation

方法起源于一种2D图形算法：

把三角形当作刚体来形变。然后再缝合。

后引申到3D：

[Sorkine and Alexa, As‐Rigid‐As‐Possible Surface Modeling. SGP 2007]

Ask all star edges to transform rigidly by some rotation R, then the shape of the cell is preserved

$$ \min_{\mathbf{v}^{\prime}}\sum_{i=1}^{n} \sum _{j\in N(i)}||({\mathbf{v}}^{\prime}_i-{\mathbf{v}}^{\prime}_j)-R_i({\mathbf{v}}_i-{\mathbf{v}}_j)||^2 $$

$$ s.t.\mathbf{v}^{\prime}_j=\mathbf{c} _j,j\in C $$

效果：

deformation 时保持 Laplacian 旋转
优点：中间会膨胀

（8） Linear Rotation‐invariant Coordinates

[Lipman et al. Siggraph 05]

保持曲面的第一形和第二形. 没听懂

• Keep a local frame at each vertex
• Prescribe changes to some selected frames

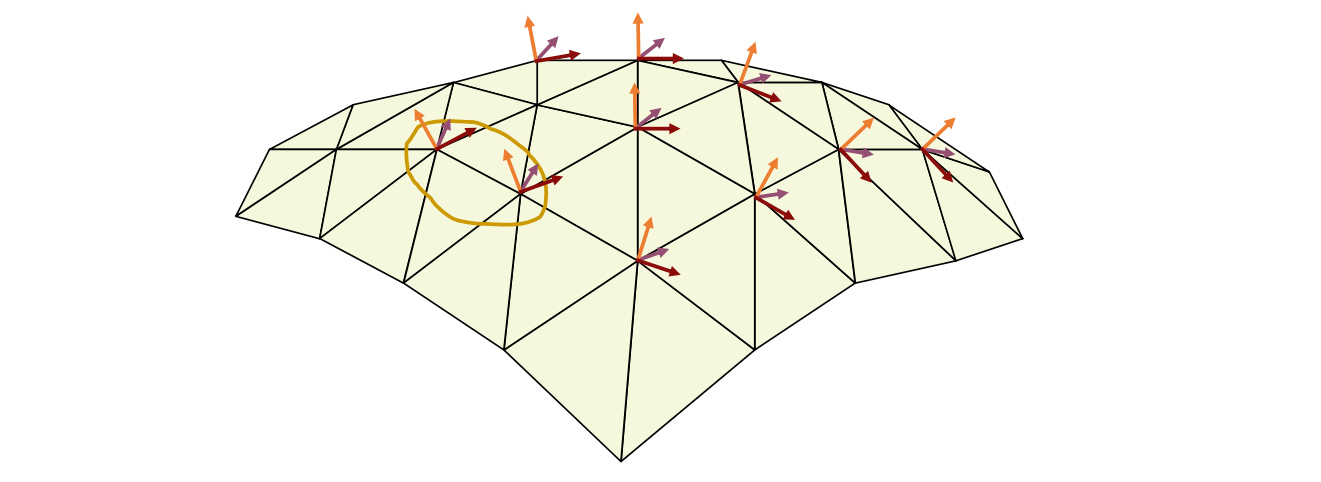
Local frame:
{\(\mathbf{a}_i, \mathbf{b}_i, \mathbf{n}_i\)}

• Encode the differences between adjacent frames
• Solve for the new frames in least‐squares sense

$$ \begin{array}{l} {\mathbf{a}_i}-{\mathbf{a}_j}=\alpha_1 {\mathbf{a}_i}+\alpha_2 {\mathbf{b}_i}+\alpha_3 {\mathbf{n}_i}\\ {\mathbf{b}_i}-{\mathbf{b}_j}=\beta _1 {\mathbf{a}_i}+\beta _2 {\mathbf{b}_i}+\beta _3 {\mathbf{n}_i} \\ {\mathbf{n}_i}-{\mathbf{n}_j}=\gamma _1 {\mathbf{a}_i}+\gamma _2 {\mathbf{b}_i}+\gamma _3 {\mathbf{n}_i} \end{array}\\ \cdots \cdots \\ constraints $$

• Reconstruction:
  • After having the frames, solve for positions Frame‐based deformations

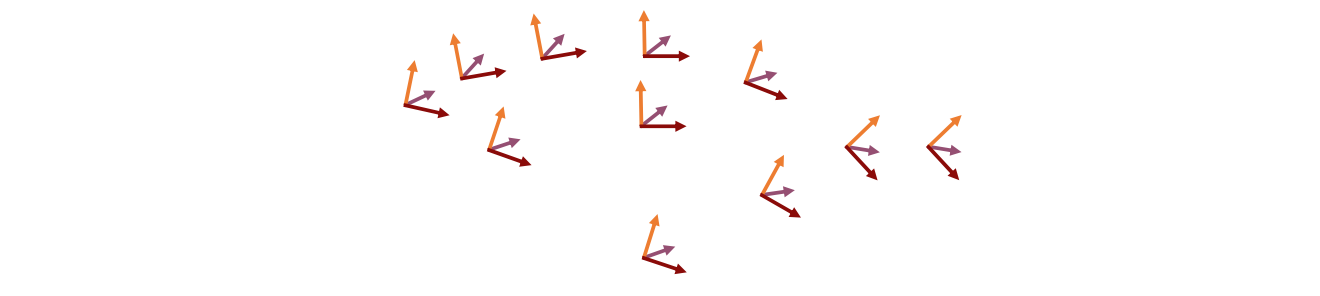
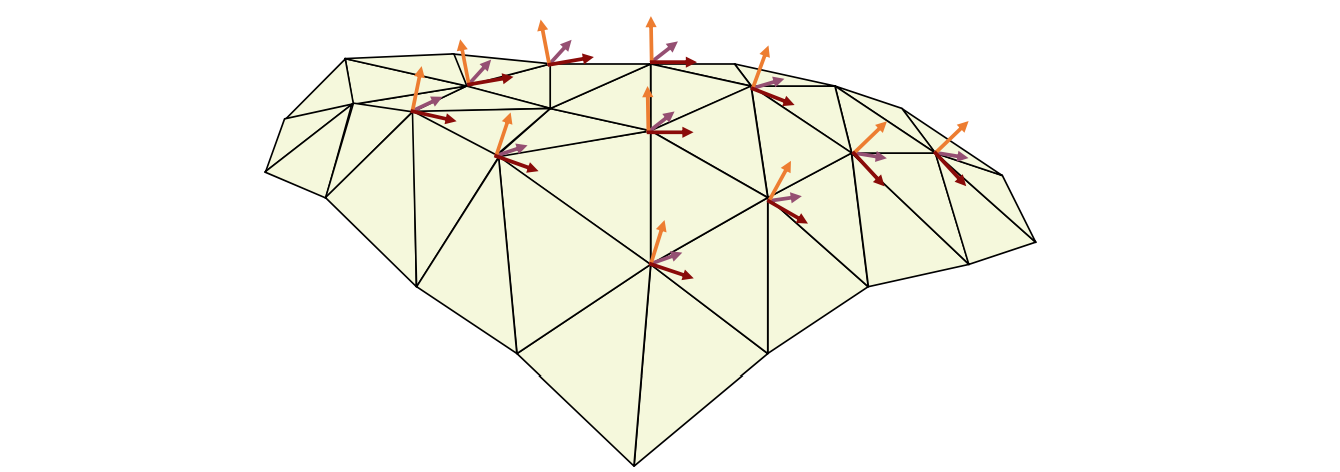
Results

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/