向量值函数

定义

🔎 [24:41]

函数的$x$称为变量，$y$称为值。如果函数的值是一个高维空间的点，或者说y是一个向量，则称为向量值函数。
x和y又分别称为自变量和应变量，因此向量值函数是多个应变量的函数。
$m$ 维向量值函数可以看作最是$m$个相互无关的普通函数

拟合方法

看成多个单变量函数，各个函数独立无关，一般会用同样的基函数（共享基函数）

$$\begin{cases} y_1=f_1(x)\\ \vdots \\ y_m=f_m(x) \end{cases}$$

✅ f1, f2, ..., fm是基于同一基函数但具有不同系数的函数。

向量值函数举例

平面/空间参数曲线

单变量

$$f:R^1 → R^m$$

$$x →\begin{pmatrix}y_1 \\\vdots \\y_m \end{pmatrix}$$

几何解释：一个实数$𝑥∈𝑅^1$映射到𝑚维空$𝑅^m$的一个点，轨迹构成$𝑅^m$的一条“曲线” ，但本质维度为1

🔎 [26:37]图

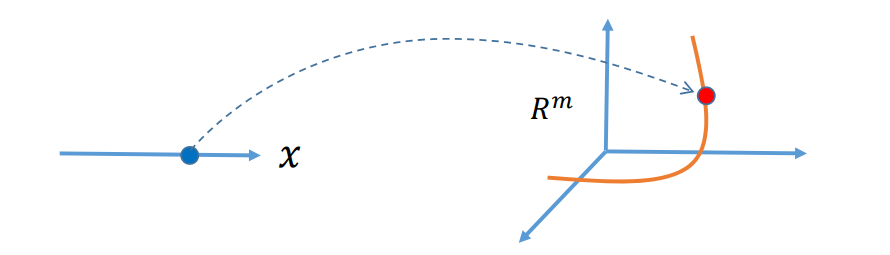
曲线的嵌入空间是高维，本质维度为1 把$x$的取值范围归一化到 [0，1]，那么任意一个$x$值对应[0，1]上的一个点。 $x 从 0 走到 1，y$在高维空间中画出一条弧线。

特例：平面参数曲线

$$f:R^1 → R^2$$

$$\begin{cases} x=x(t)\\ y=y(t) \end{cases}$$

$$t\in [0,1]$$

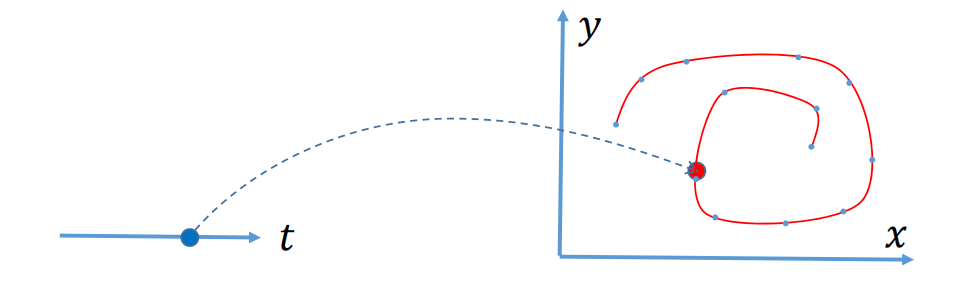
在这一页中， $t 是变量，(x,y)$是值　　

特例：空间参数曲线

$$f:R^1 → R^3$$

$$\begin{cases} x=x(t) \\ y=y(t) \\ z=z(t) \end{cases}$$

$$t\in [0,1]$$

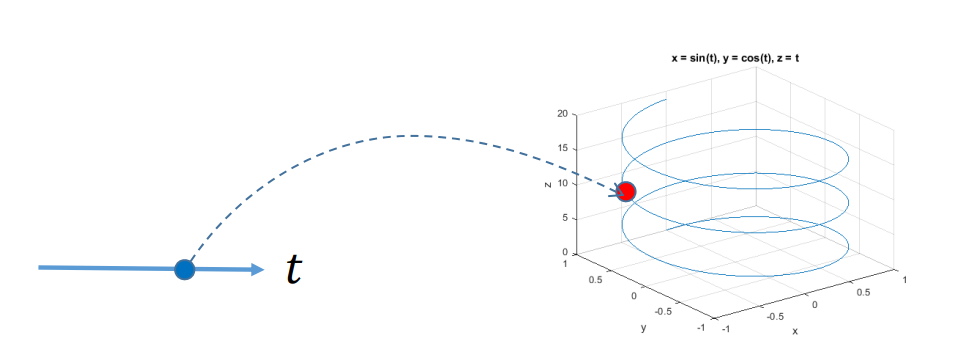
参数曲面

$$f:R^2 → R^3$$

$$\begin{cases} x=x(u,v) \\ y=y(u,v) \\ z=z(u,v) \end{cases}$$

$$(u,v)\in [0,1]\times [0,1]$$

几何解释：
• 一张曲面由两个参数$(u,v)$决定，也称为双参数曲面
• 可灵活表达非函数型的任意曲面

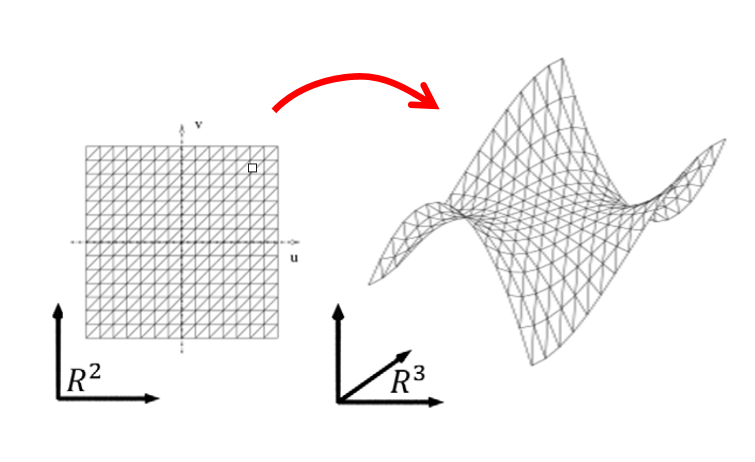
流形：任意一个点的无穷小区域，等价于二维平面的圆盘
[32:28] 三维流形曲面，本质上是二维。

二维映射

$$f:R^2 → R^2$$

$$\begin{cases} x=x(u,v) \\ y=y(u,v) \end{cases}$$

$$(u,v)\in [0,1]\times [0,1]$$

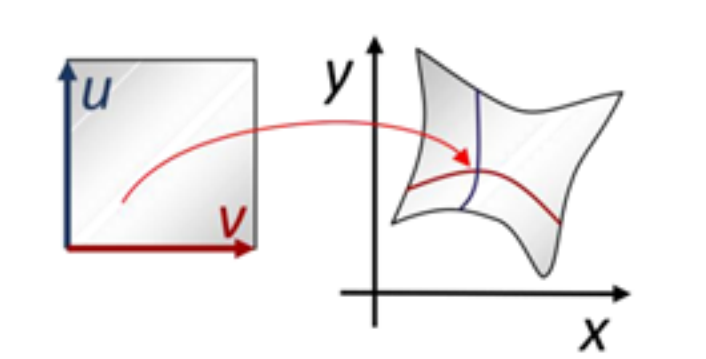
几何解释：二维区域之间的映射，可看成特殊的曲面（第三个维度始终为$0$）
应用：图像变形(warping)

三维映射

$$f:R^3 → R^3$$

$$\begin{cases} x=x(u,v,w)\\ y=y(u,v,w) \\ z=z(u,v,w) \end{cases}$$

$$(u,v,w)\in [0,1]^3$$

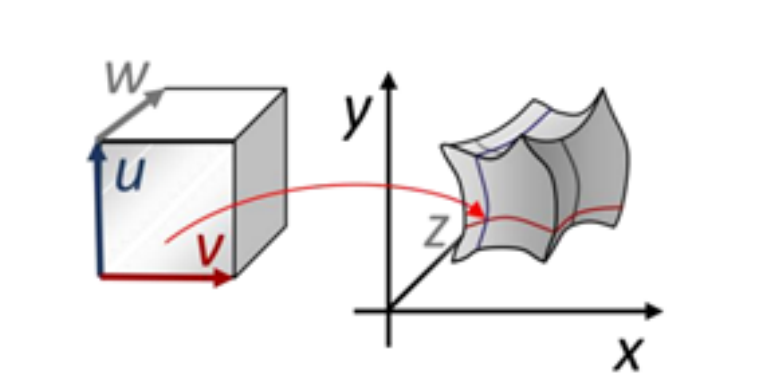
几何解释：三维体区域之间的映射
应用：体形变、体参数化、有限元

降维映射（低维投影）

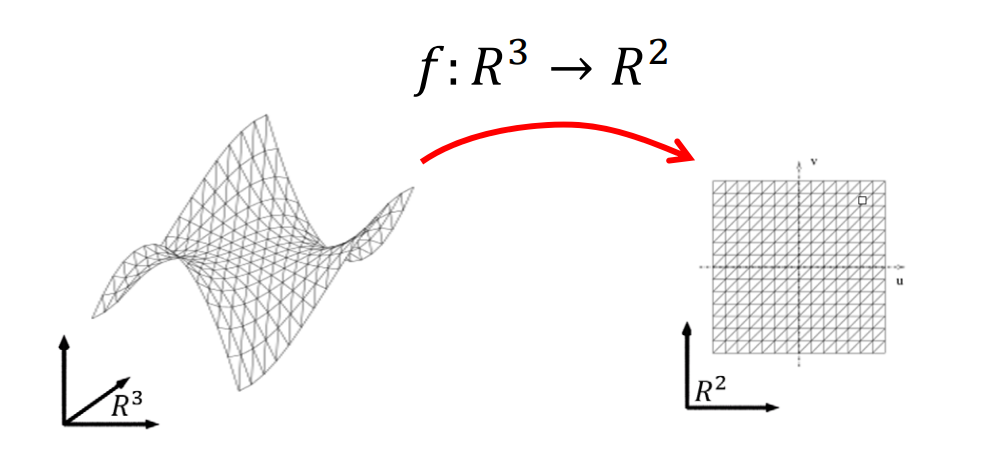
降维映射一般有信息丢失，丢失的信息大部分情况下不可逆，即无法恢复

高维到低维，如果多个点映射到一个点，就会发生信息丢失，不可恢复。 　　　

💡 我的思考
信息丢失不定是坏事，有可能本身就是一个点，由于躁声的原因表现为多个点，也有可能是次要信息，不希望提取出­来。

一般映射

$$f:R^n → R^m$$

• $n<m$
  为低维到高维的映射（高维的超曲面，$n$维流形曲面），本征维度为$n$
• $n>m$
  为降维映射，一般信息有损失
  （1）如果$𝑅^n$中的点集刚好位于一个$𝑚$维（或小于$𝑚$）的流形上，则映射可能是无损的，即可以被恢复的
  （2）如果值维度低于变量的本质维度，则必定不可恢复。

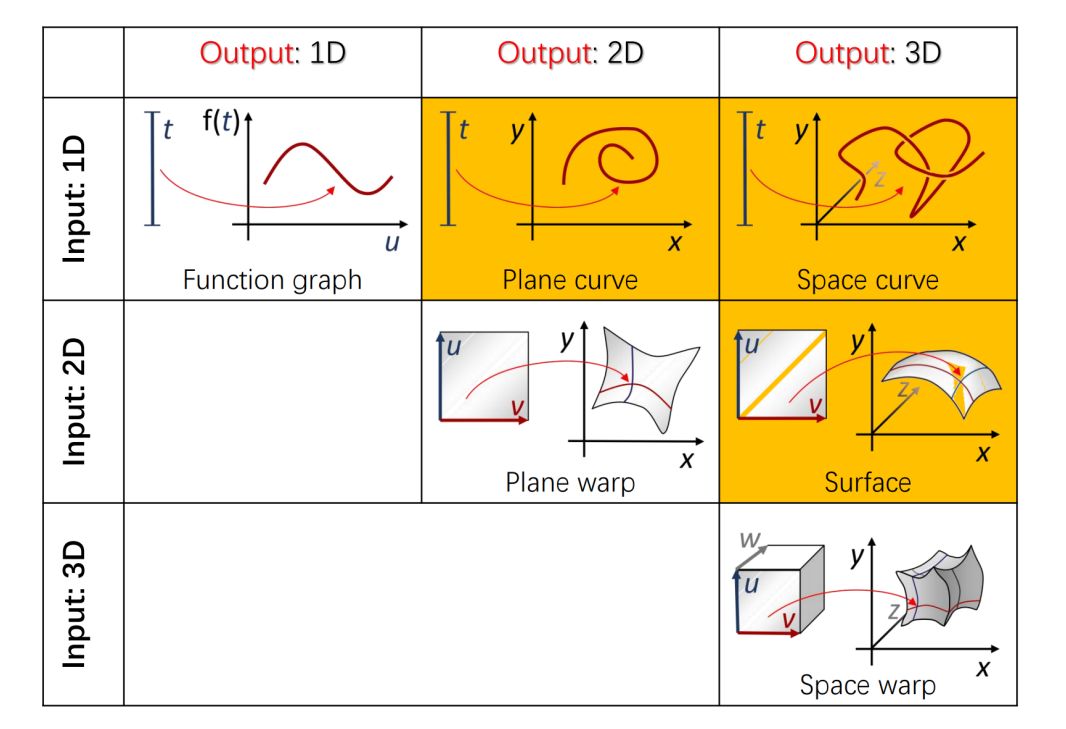
[42：00] 其中黄色为参数学习曲面

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/