曲线拟合问题
问题描述
[42:43]
输入:给定平面上系列点\((x_i,y_i),i=1,2,...,n\)
输出:一条参数曲线,拟合这些点
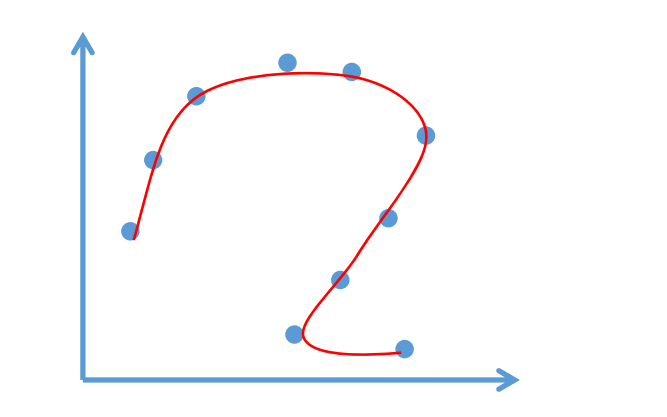
👆 [42:50]非函数型曲线
解决方法
$$ f:R^1 → R^2 $$
$$ \begin{cases} x=x(t)\\ y=y(t) \end{cases} $$
$$ t\in [0,1] $$
存在的问题
❓ \(x=x(t)\),用\(x(t)\)拟合数据点\(x_i\),但\(x_i\)与\(t\)没有关系,如何拟合?
答:需要人为构造这个关系。即构造\((t_i,x_i)\),这个过程称为参数化,\(t_i\)是参数。
即,\(x(t)\)拟合点\((t_i,x_i)\),\(y(t)\)拟合点\((t_i,y_i)\)
基于曲线参数化的曲线拟合问题
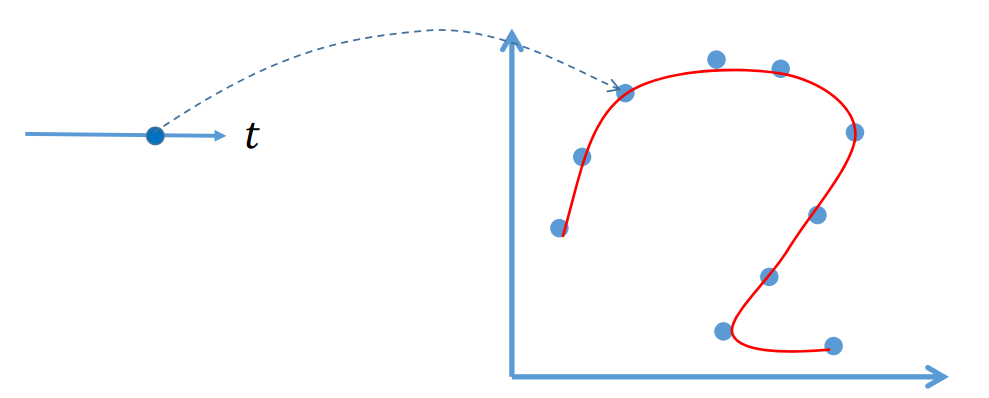
$$ \begin{cases} x=x(t)\\ y=y(t) \end{cases} $$
$$ t\in [0,1] $$
矢量符号化表达: $$ p=p(t)=\binom{x(t)}{y(t)} $$
然后极小化误差度量:
$$ E= {\textstyle \sum_{i=1}^{n}} ||\binom{x(t_i)}{ y(t_i)}-\binom{x_i}{y_i} ||^2= {\textstyle \sum_{i=1}^{n}}||p(t_i)-p_i||^2 $$
曲线参数化
构造\((t_i,x_i)\)和\((t_i,y_i)\)主要是如何取\(t_i\)
通常\(t_0=0,t_n=1\)
❓ 对数据点\((x_i,y_i)\),对应哪个参数\(𝑡_i\)?
答:求数据点所对应的参数(点列的参数化):一个降维的问题!
下面的参数化方法以二维为例。
均匀参数化 Equidistant (uniform) parameterization
\(𝑡_{i+1}-𝑡_i=const\)
例如:\(𝑡_i=i\),得到的点对为{(1,x1),(2,x2),...,(n,xn)}和{(1,y1),(2,y2),...,(n,yn)}
缺点:Geometry of the data points is not considered
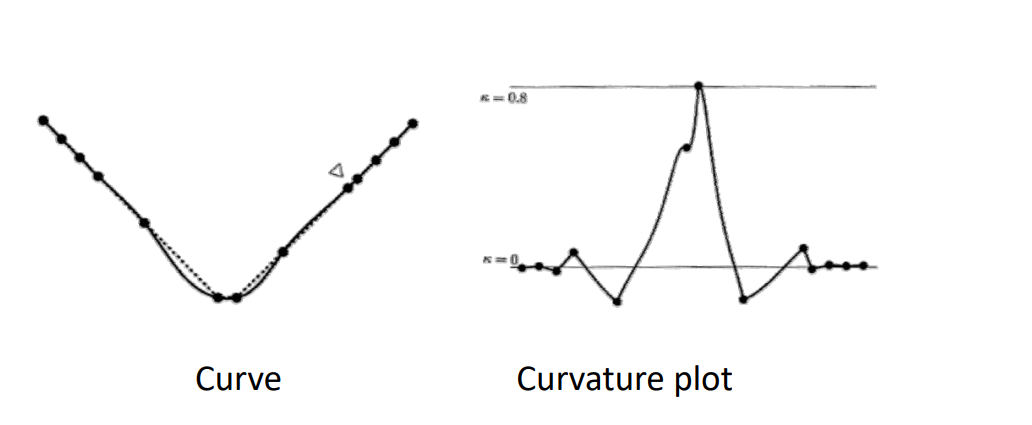
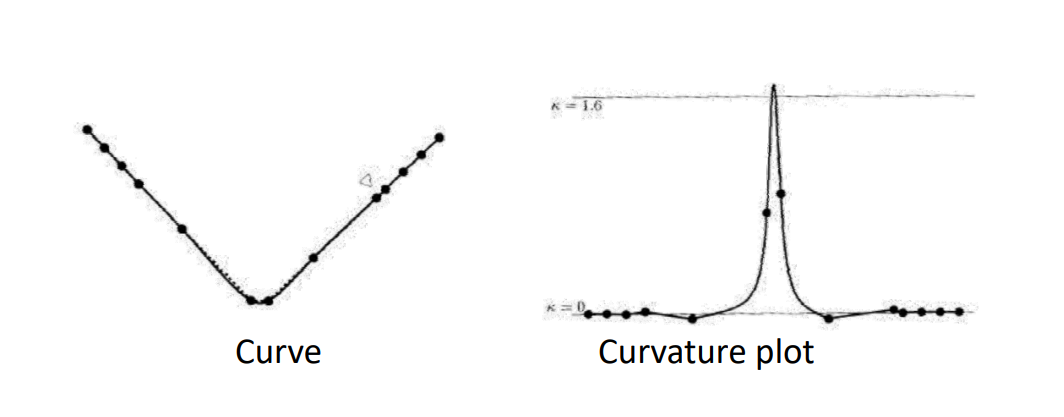
👆 用 uniform 角处比较尖锐,更好的参数化方法会得到更平滑的曲线。
弦长参数化 Chordal parameterization
\(𝑡_{i+1}-𝑡_i=||k_{i+1}-k_i||\)
Chordal 参数的距离与邻居点的距离成正比
中心参数化 Centripetal parameterization
\(𝑡_{i+1}-𝑡_i=\sqrt{||k_{i+1}-k_i||} \)
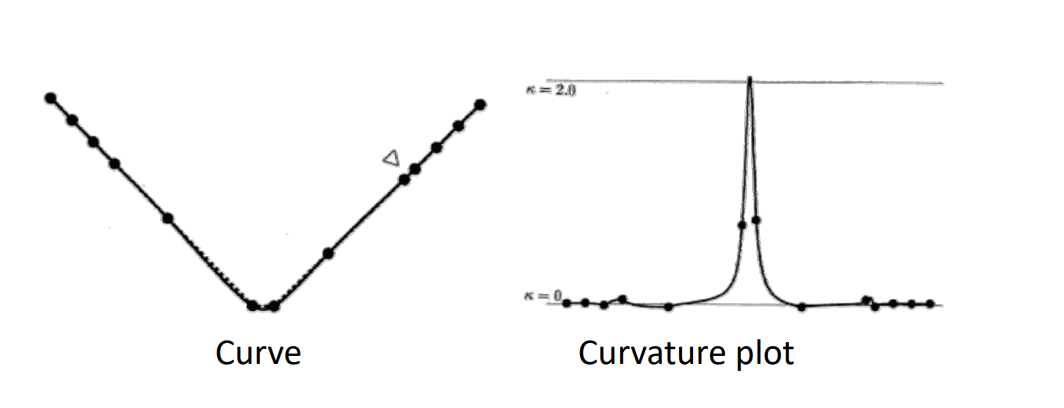
老师没有解释这种方法
Foley parameterization
老师没有解释这种方法
Involvement of angles in the control polygon
$$ t_{i+1}-t_i = ||k_{i+1}-k_i|| \cdot \left(1+\frac{3}{2} \frac{\hat\alpha_i ||k_{i} - k_{i-1}||}{||k_{i}-k_{i-1}||+||k_{i+1}-k_i||}+\frac{3}{2} \frac{\hat\alpha_{i+1}||k_{i+1}-k_i||}{||k_{i+1}-k_i||+||k_{i+2}-k{i+1}||} \right) $$
with
$$ \hat{\alpha } _i=\min (\pi -\alpha _i,\frac{\pi }{2} ) $$
and
$$ \alpha_{i}=angle(k_{i-1},k_i,k_{i+1}) $$
四种方法的比较
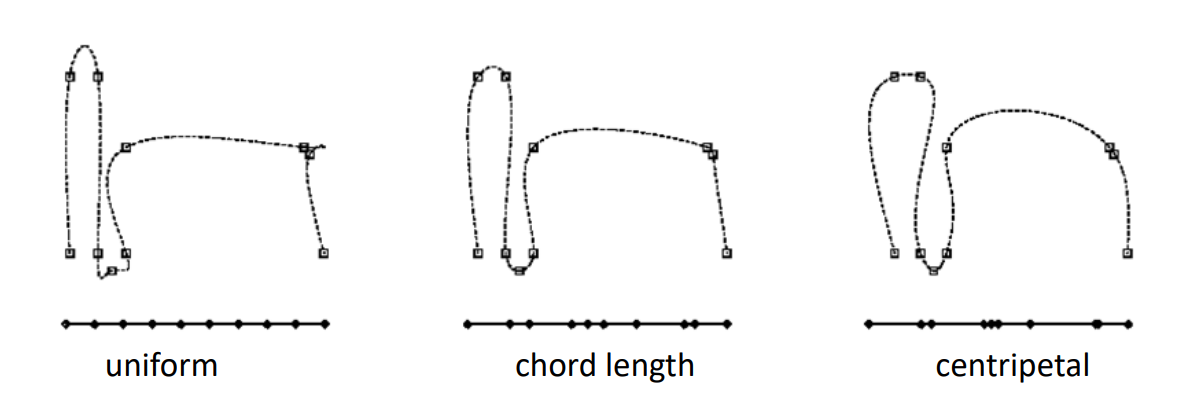
点的参数化对曲线拟合的影响很大,需要好的参数化!
按照老师的意思,似乎得到的曲线越光滑,说明参数化越好。
参数化的本质是降维。即把曲线原本所在的空间,嵌入到参数空间。
如果降维的维度不对,或维度对了但分布不好,都会导致降维结果不好。[58:40]
曲面参数化
三维的点找二维的参数:一个降维的问题!
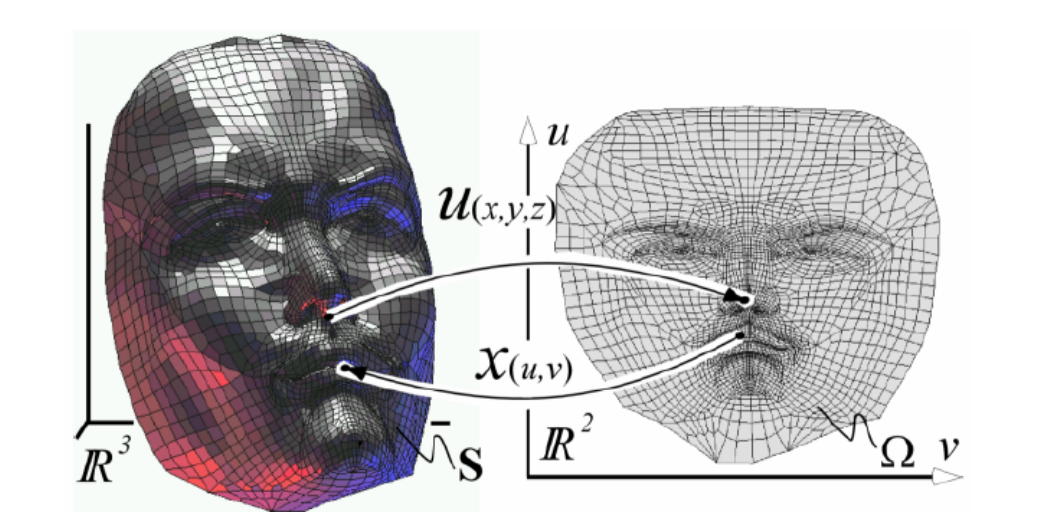
参数化约束:保持边长、网格面积、角度,就能得到比较好的参数结果。
曲面参数化的应用
- 纹理映射

- 地图绘制
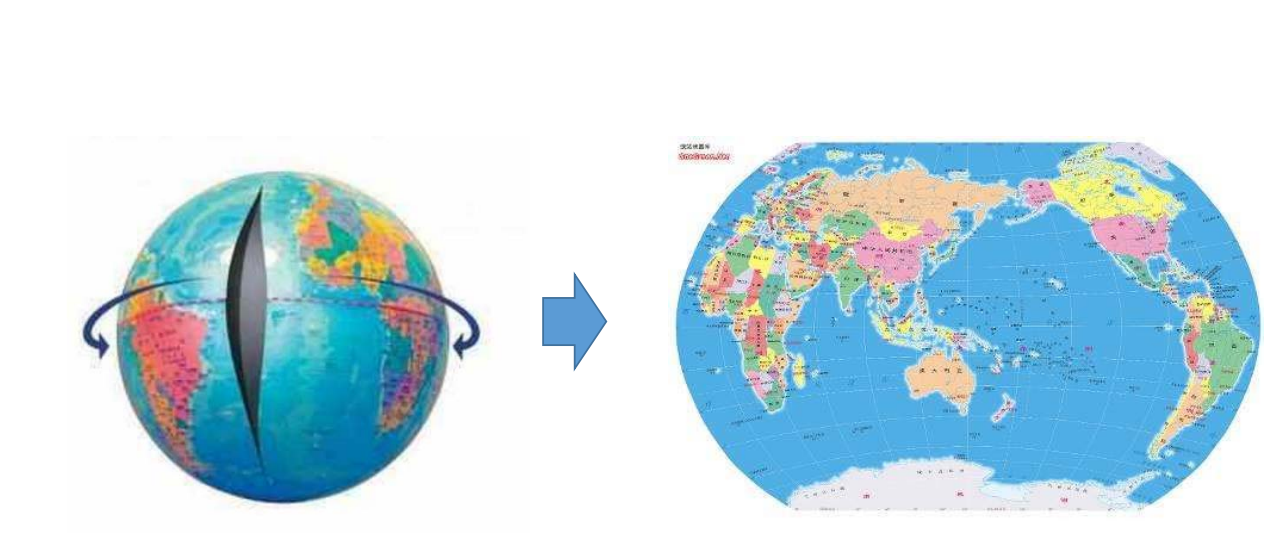
可展曲面展成平面不会扭曲。
球面不可展,展开必定扭曲。
本文出自CaterpillarStudyGroup,转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/