离散微分几何要解决的问题

微分几何研究曲面无穷小邻域上的微分属性（导数、曲率）
但Mesh是分段线性的，在三角形内部无穷连续，在边和点上$C^0$连续。
$C^0$连续不光滑、不可微，如何讨论微分性质？

答：通过采样点估计出原始曲面的微分属性。包括：
• Normal estimation
• Curvature estimation
• Principal curvature directions
• …

两种估计微分属性的方法论

Approximate the (unknown) underlying surface

（1） Continuous approximation：Approximate the surface & compute continuous differential measures (normal, curvature)
（2） Discrete approximation：Approximate differential measures for mesh

Continuous Approximation

Quadratic Approximation

第一步：获取周围点的信息

对于要估计的顶点，使用其周围的顶点的信息：

Compute normal at vertex
- Typically average face normals
Compute tangent plane & local coordinate system
For each neighbor vertex compute location in local system
- relative to node and tangent plane

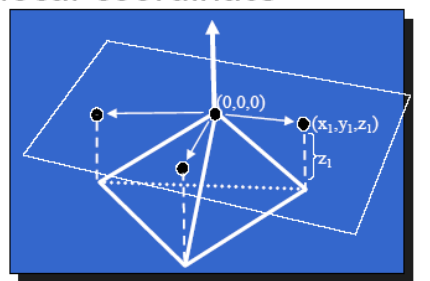
第二步：拟合曲面

定义 quadric function，例如抛物面

$$ F(x, y, z)=ax^{2}+bxy+cy^{2}-z=0 $$

使用least squares来找到拟合quadric function的系数

$$ \min \sum_{i}^{} (ax_i^2+bx_iy_i+cy_i^2-z_i) $$

$$ \begin{pmatrix}x_1^2 & x_1y_1 &y_1^2 \\ \cdots &\cdots &\cdots \\ x_n^2 &x_ny_n &y_n^2 \end{pmatrix}\begin{pmatrix}a \\b \\c \end{pmatrix}=\begin{pmatrix}z_1 \\\cdots \\z_n \end{pmatrix}A=\begin{pmatrix}x_1^2 & x_1y_1 &y_1^2 \\ \cdots &\cdots &\cdots \\ x_n^2 &x_ny_n &y_n^2 \end{pmatrix},X=\begin{pmatrix}a \\b \\c \end{pmatrix},b=\begin{pmatrix}z_1 \\\cdots \\z_n \end{pmatrix} $$

Approximation can be found by:$\tilde{X}=\left(A^{T} A\right)^{-1} A^{T} b$

第三步：基于曲面估计微分属性

Approximation principal curvatures

Given surface $F$，principal curvatures $k_\min $ and $k_\max$ are real roots of:

$$ k^{2}-(a+c)k + ac - b^{2} = 0 $$

Mean curvature:

$$ H = (k_\min + k_\max)/2 $$

Gaussian curvature:

$$ K = k_\min k_\max $$

Other approximation

Cubic approximation
• J. Goldfeather and V. Interrante. A novel cubic‐order algorithm for approximating principal direction vectors. ACM Transactions on Graphics 23, 1 (2004), 45–63.
Implicit surface approximation
• Yutaka Ohtake et al. Multi‐level partition of unity implicits. Siggraph 2003.
Many others…

Discrete Approximation

顶点的Normal Estimation

顶点Normal = 加权平均 face normals

Weighted: face areas, angles at vertex

What happen at edges/creases(折痕)?
为什么刘老师要问这个问题，顶点肯定在边上的。

Mean Curvature

由Laplace‐Beltrami（平均曲率流）定理：

$$ K(x_i)=\frac{1}{2A_M} \sum_{j\in N_1(i)}^{} (\cot \alpha _{ij}+\cot \beta _{ij})(x_i-x_j) $$

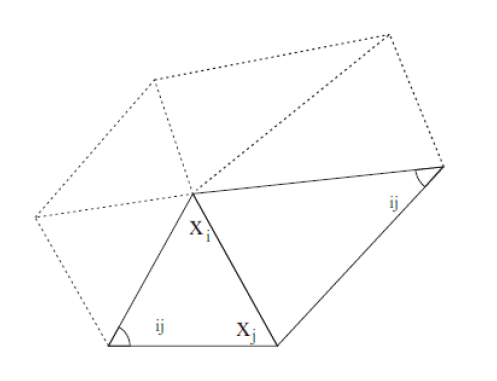
其中：
$N_l(X_i)$:表$X_i点的l$邻域点
$A_m$：整个多边形的面积

Gauss Curvature

Gauss‐Bonnet定理：

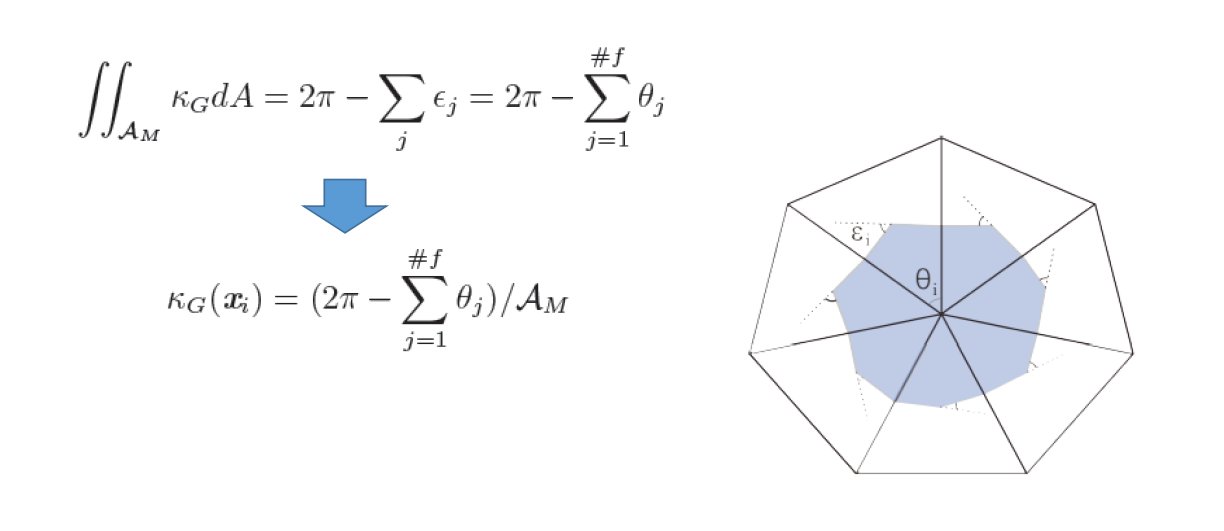
例子：

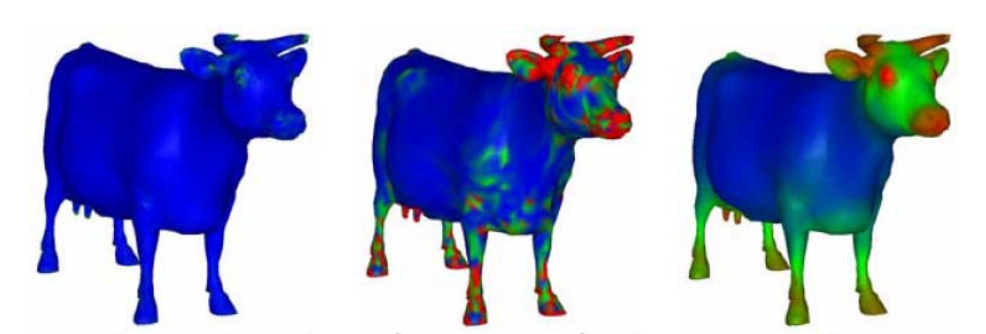
👆 color map：数据的可视化方法，红 > 绿 > 篮

存在的问题

Approximation always results in some noise
解决方法：（1）截断（2）平滑

References

MEYER M., DESBRUN M., SCHRÖDER P., BARR A.: Discrete differential‐geometry operators for triangulated 2‐manifolds. In Visualization and Mathematics III, Hege H.‐C., Polthier K., (Eds.). Springer, 2003, pp. 35–58. (PDF)

离散微分几何算子的开创性文章

TAUBIN G.: Estimating the tensor of curvature of a surface from a polyhedral approximation. In Proc. International Conference on Computer Vision (1995), pp. 902–907.
MEYER M., DESBRUN M., SCHRÖDER P., BARR A.: Discrete differential‐geometry operators for triangulated 2‐ manifolds. In Visualization and Mathematics III, Hege H.‐C., Polthier K., (Eds.). Springer, 2003, pp. 35–58.
CAZALS F., POUGET M.: Estimating differential quantities using polynomial fitting of osculating jets. In Eurographics Symposium on Geometry Processing (2003), pp. 177–187.
COHEN‐STEINER D., MORVAN J.: Restricted delaunay triangulations and normal cycle. In Proc. ACM Symposium on Computational Geometry (2003), pp. 312–321.
GOLDFEATHER J., INTERRANTE V.: A novel cubic‐order algorithm for approximating principal direction vectors. ACM Transactions on Graphics 23, 1 (2004), 45–63.
MARTIN R. R.: Estimation of principal curvatures from range data. International Journal of Shape Modeling 4, 1 (1998), 99–109.
OHTAKE Y., BELYAEV A., SEIDEL H.‐P.: Ridge‐valley lines on meshes via implicit surface fitting. ACM Transactions on Graphics 23, 3 (2004), 609–612. (Proc. SIGGRAPH’2004).
PAGE D., SUN Y., KOSCHAN A., PAIK J., ABIDI M.: Normal vector voting: Crease detection and curvature extimation on large, noisy meshes. Graphical Models 64, 3‐4 (2002), 199–229.

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/