曲面的微分几何

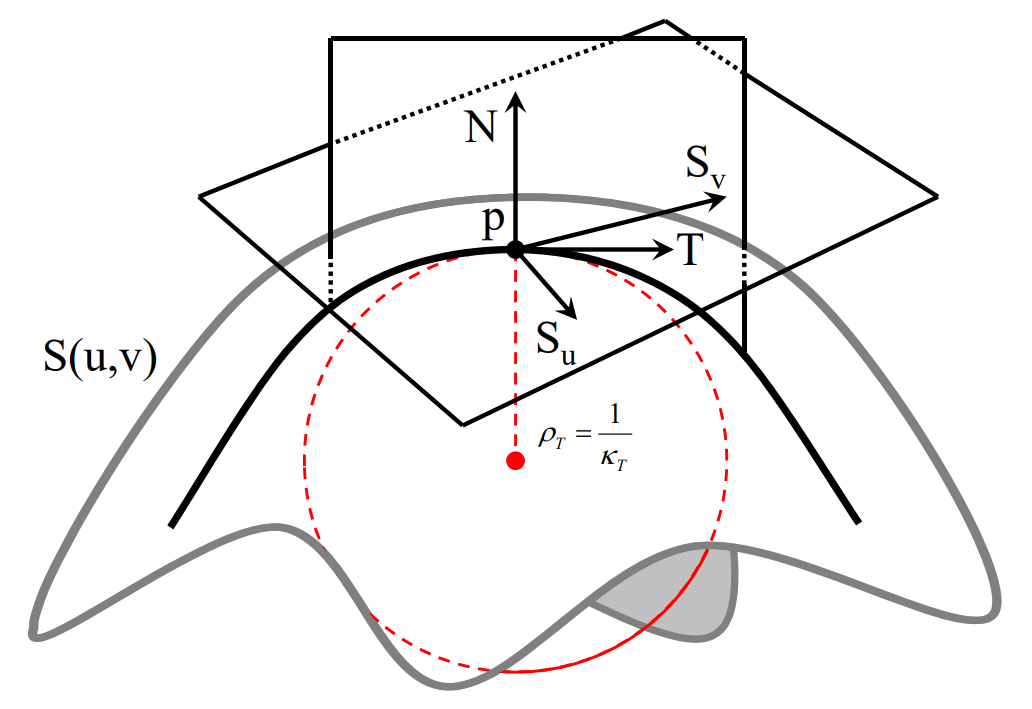
Point p

Point p on the surface at $(u_0,v_0)$

Tangent $S_u$

Tangent $S_u$ in the u direction

$$ S_u=\frac{\partial S(u,v)}{\partial u} $$

Tangent $S_v$

Tangent $S_v$ in the v direction

$$ S_v=\frac{\partial S(u,v)}{\partial v} $$

Plane of tangents T

$$ T=uS_u+vS_v $$

$S_u 和 S_v$ 张成一个平面，称为切平面。

Normal N

$$ N=\frac{S_u\times S_v}{||S_u\times S_v||} $$

Curvature

方向曲率：曲率是随着方向变化的

N 所在平面与曲面相交，得到平面曲线，有对应的曲率空间曲面的切线和曲率都是基于特定方向的。

曲面的曲率

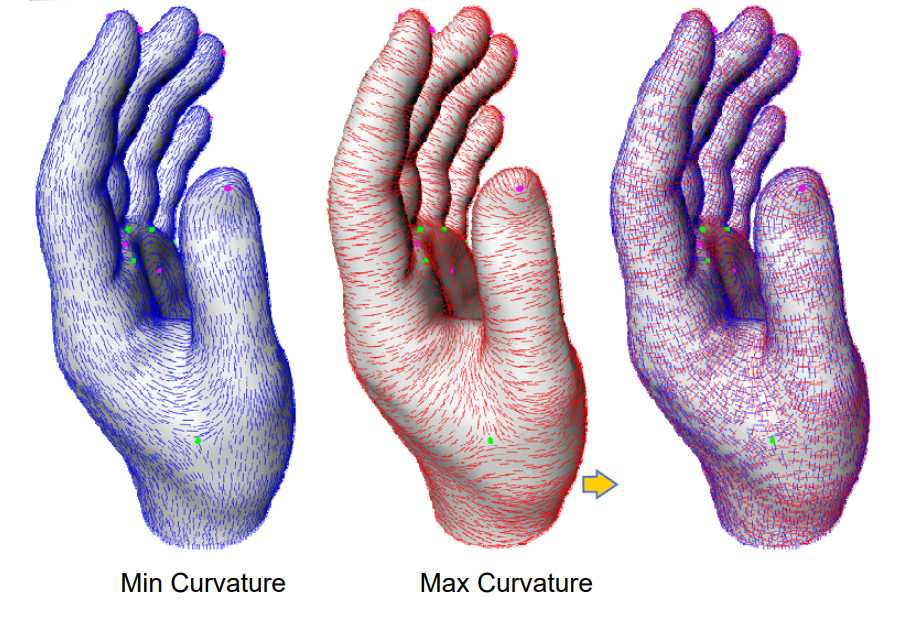
主曲率 Principal Directions

两个方向（正交）曲率：最大曲率$𝜅_1$和最小曲率$𝜅_2$

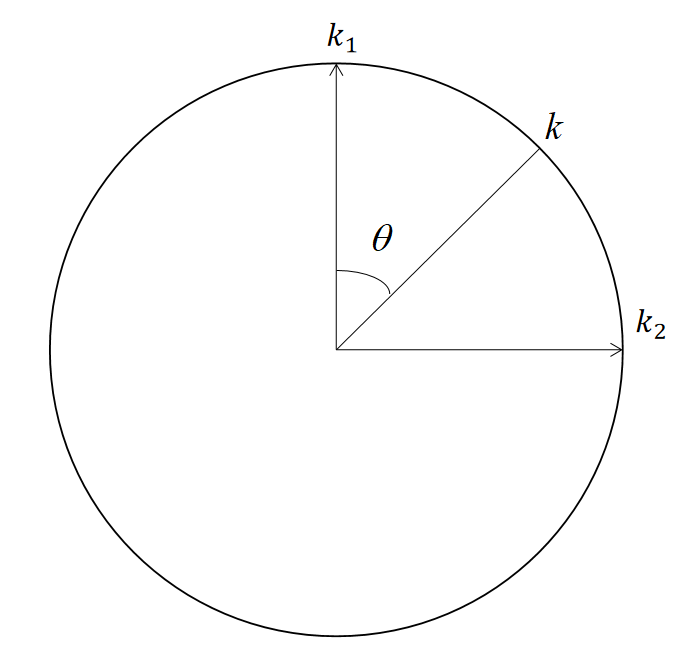
其他方向曲率：

$$ k=k_1\cos ^2\theta +k_2\sin ^2\theta $$

$\theta $是当前曲率方向与$K_1$方向的夹角。

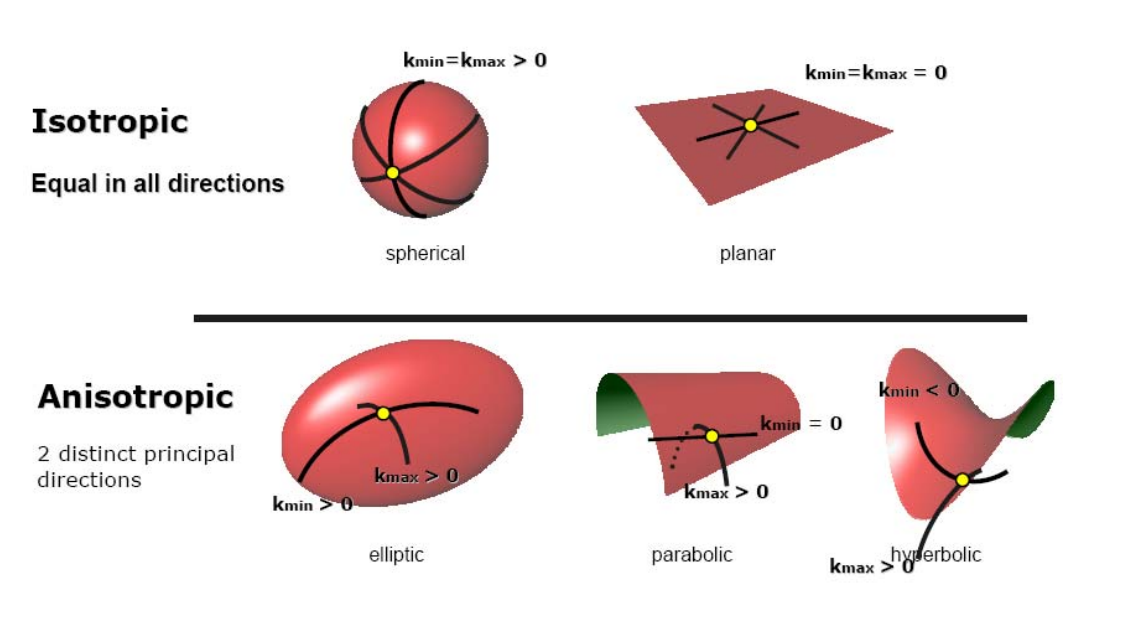
高斯曲率

$$ k=k_1k_2 $$

等距变换不变量：曲面发生变形，但曲面上任意两点间距离不变。

可展曲面：处处高斯曲率为0的曲面。其展开为平面时不会发生变形。
有三类可展曲面：柱面、锥面、切线面

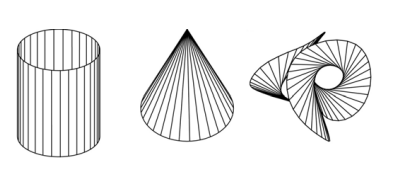
切线面：任意空间曲线的所有切线构成的面。

平均曲率

$$ k=\frac{k_1+k_2}{2} $$

处处平均曲率为0的曲面：极小曲面

平均曲率流定理

$$ \delta _i=\frac{1}{d_i} \sum _{\nu\in N(i)}(\nu_i-\nu) $$

$$ \frac{1}{len(\gamma )} \int _{\nu\in \gamma }(\nu_i-\nu)ds $$

$$ \lim_{len(\gamma ) \to 0} \frac{1}{len(\gamma )} \int _{\nu\in \gamma }(\nu_i-\nu)ds=H(\nu_i)n_i $$

$\gamma $代表红点的邻域外围封闭曲线。
$V_i 是红点， V是\gamma $上的点。
$ len(\gamma) $代表曲线长度。
$H(V_i)为 V_i$ 的平均曲率。

当曲线长度趋于0，其极限是一个常值。常值的方向为法向，大小为平均曲率。

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/

GAMES102