细分曲线的性质证明

证明的思路

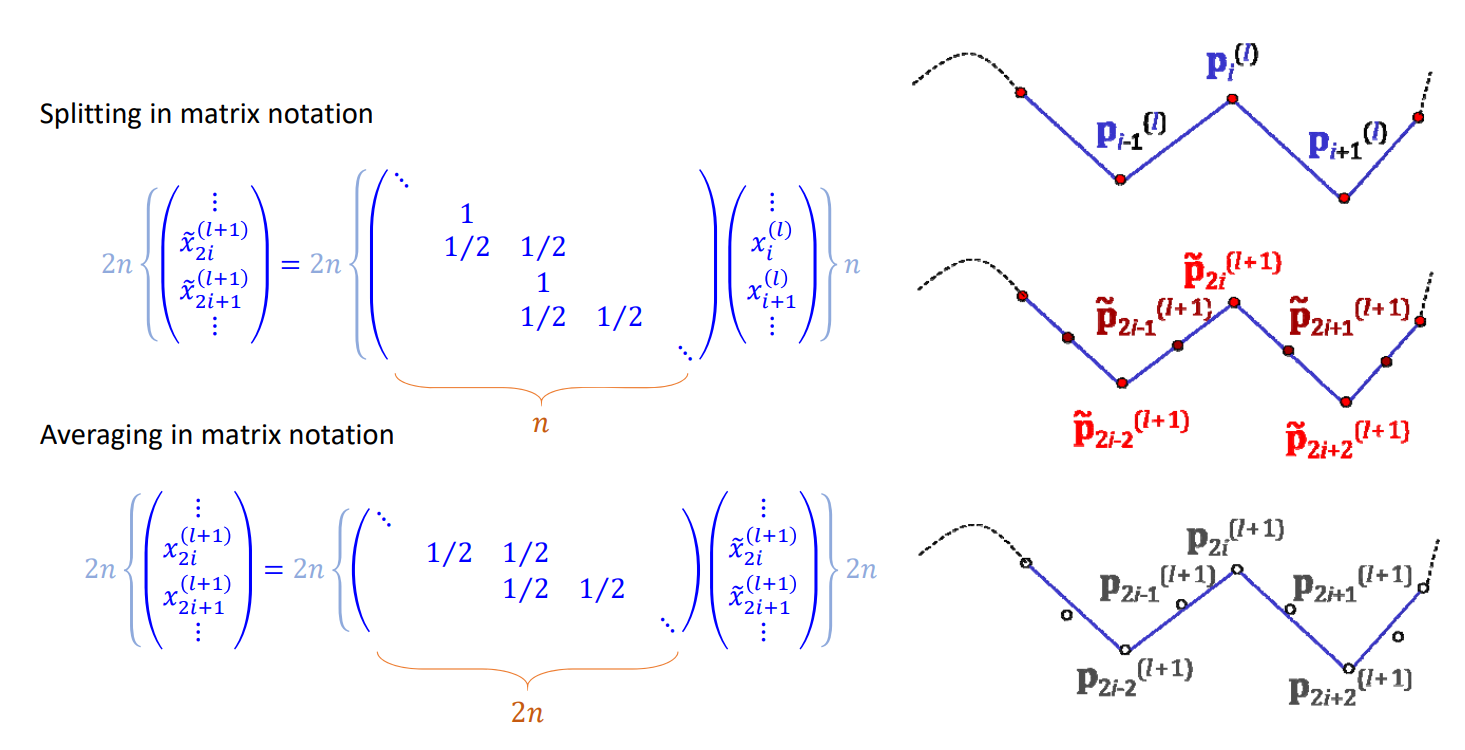
新顶点是老顶点的线性组合，据此将细分过程表达成矩阵形式
讨论细分矩阵的谱性质（特征根）

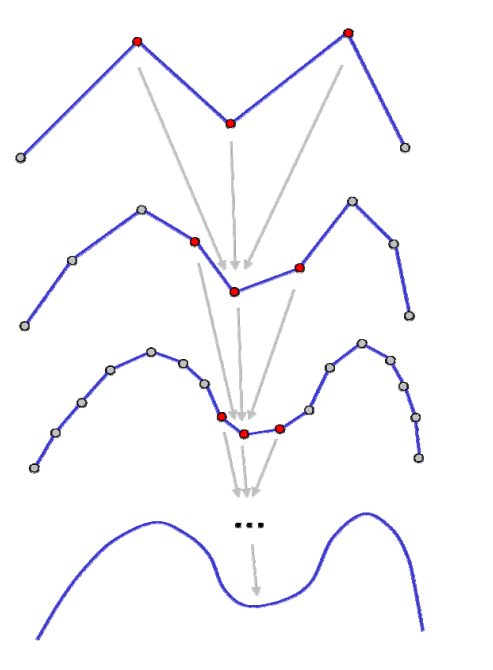
[41:07]证明的思路
这个感受野不离断变大的过程像卷积。

Chaikin细分

矩阵形式

Control points at level   $𝑙: 𝒑^{(l)}_i$

“Splitted” points at level $𝑙+1: \tilde{p} ^{(l+1)}_i$

“Averaged” control points at level $𝑙+1:𝒑^{(l+1)}_i$

极限情况

极限曲线上的点可由细分矩阵的幂次的极限求得:

$$\begin{pmatrix}x_-^{[\infty ]}  \\x^{[\infty ]}  \\x_+^{[\infty ]} \end{pmatrix}=\lim_{k \to \infty} M^k_{srbdiv}\begin{pmatrix}x_-^{[l]}  \\x^{[l]}  \\x_+^{[l ]} \end{pmatrix}$$

• 收敛的必要条件:
  • 细分矩阵的最大特征根为1
  • 否则会爆炸 (>1) 或收缩 (<1)

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/