1. Vertex Filtering
1.1 Laplacian Smoothing
原理
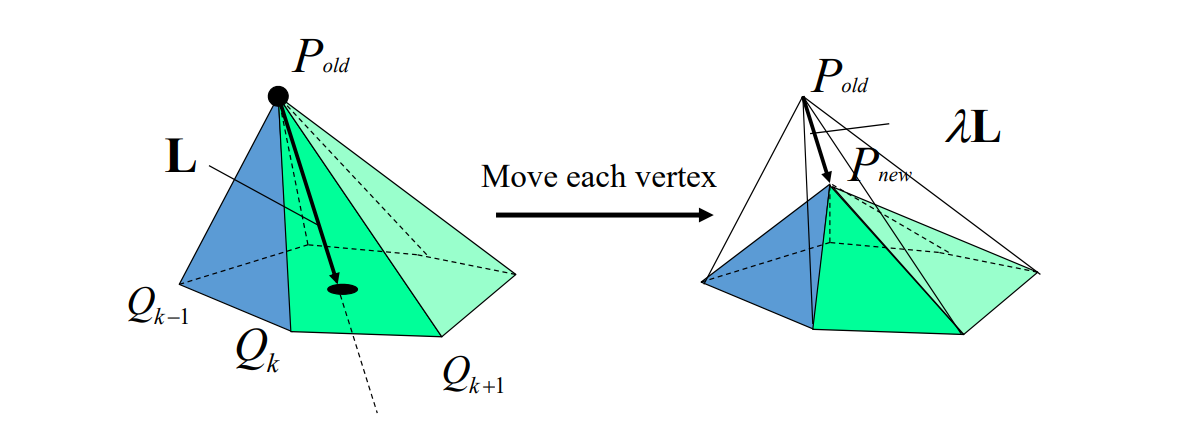
特点
- Equivalent to box filter in signal processing
- Apply to all vertices on mesh
- Typically repeat several times
- Can describe as energy minimization
• Energy = sum of squared edge lengths in mesh
• Parameter\(\lambda >0\)controls convergence "speed"
存在的问题
存在Over‐smoothing问题
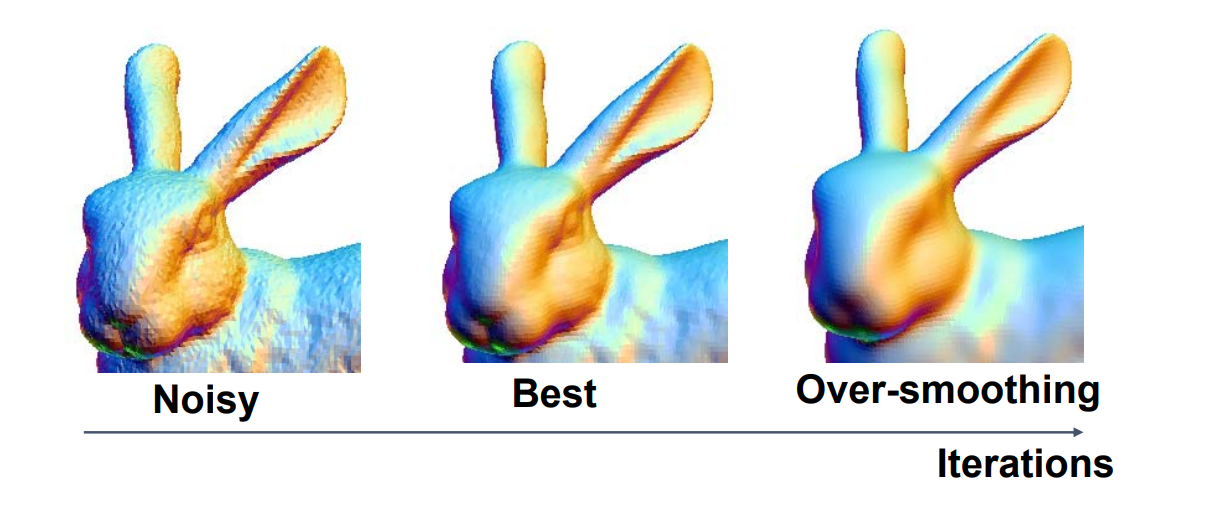
存在Shrinkage问题
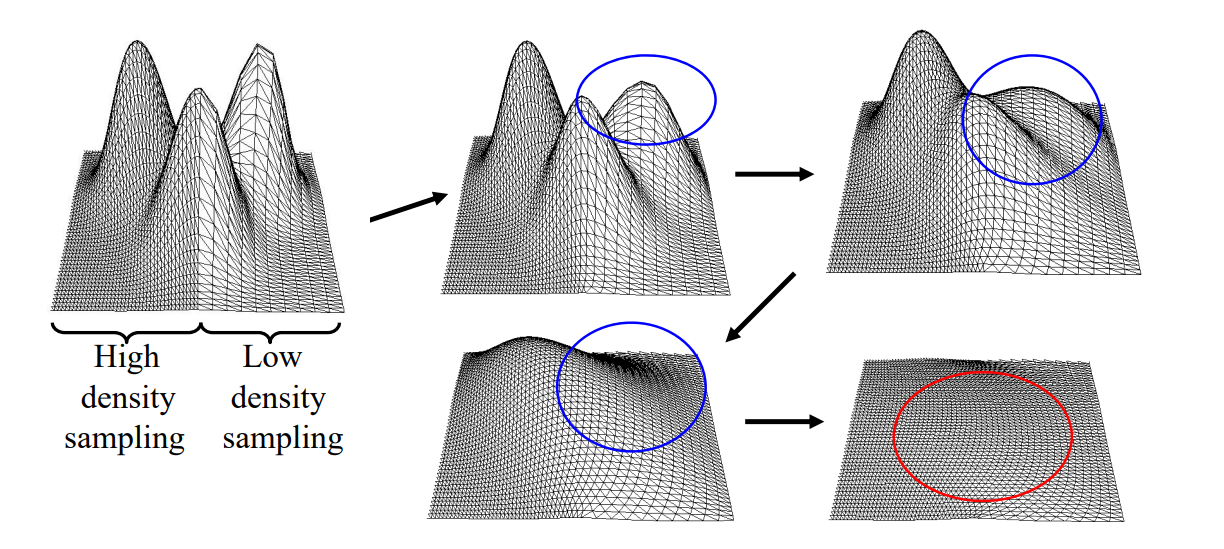
改进
- Laplacian
$$ P^{new} = P^{old}+\lambda L(P^{old}) $$
- Taubin’95:Laplacian + Expansion
$$ P^{new} = P^{old}-(\mu -\lambda )L(P^{old})-\mu \lambda L^2(P^{old}),\mu >\lambda >0 $$

图1:原图
图2:普通 Laplace
图3:Laplace + 收缩完再扩张回去。去噪同时保留了一些特征。
- Bilaplacian:Special case of Taubin’s
$$ P^{new} = P^{old}+\lambda L^2(P^{old}) $$
两阶拉普拉斯
1.2 Mean Curvature Flow
引入平均曲率、考虑了几何特征。
1.3 Bilateral filtering 双边滤波
此方向借鉴于图像算法
图像算法是的双边滤波
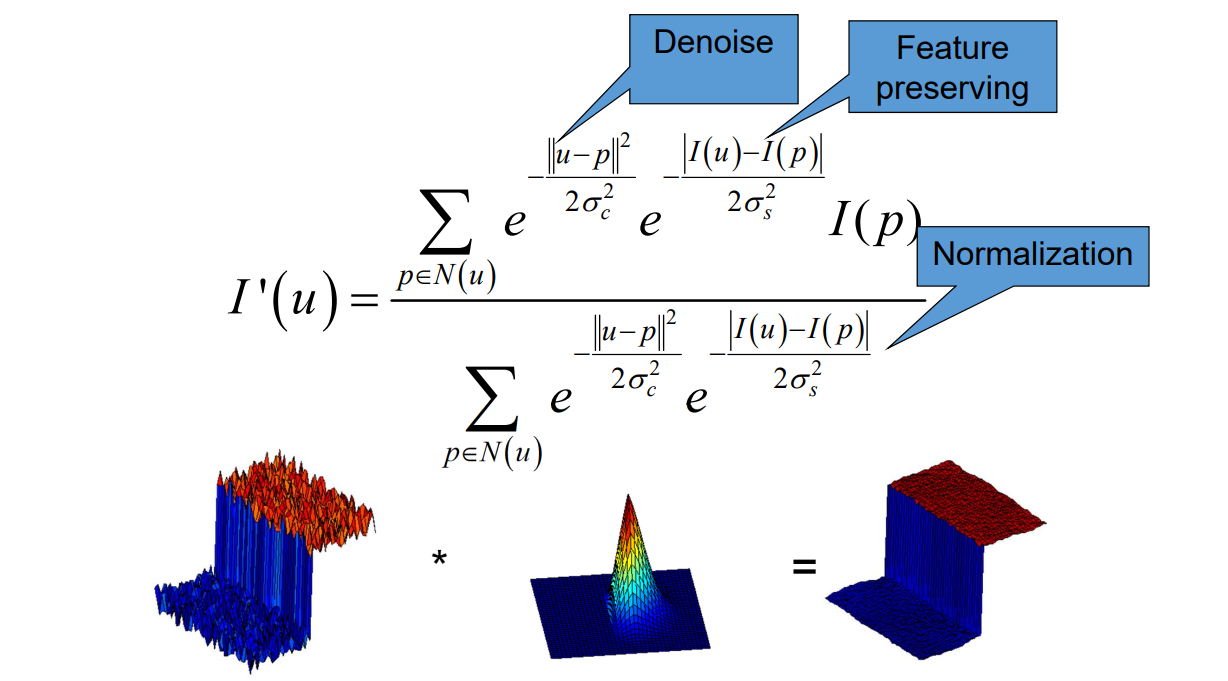
Bilateral:双边
U 和 P 代表U点与P点的位置
I(U) 和I(P)代表U和P点的值
分子:U 点对 P 点的影响表现I(P)前面的系数上。
系数考虑了两方面因素:
(1) U 与 P 的距离,反映了U 对 P 的影响力。
(2) I(U) 与I(P)的距离,反映了I(P)的特征性。
二者都是距离越大权重越小。
分母,归一化
例子:
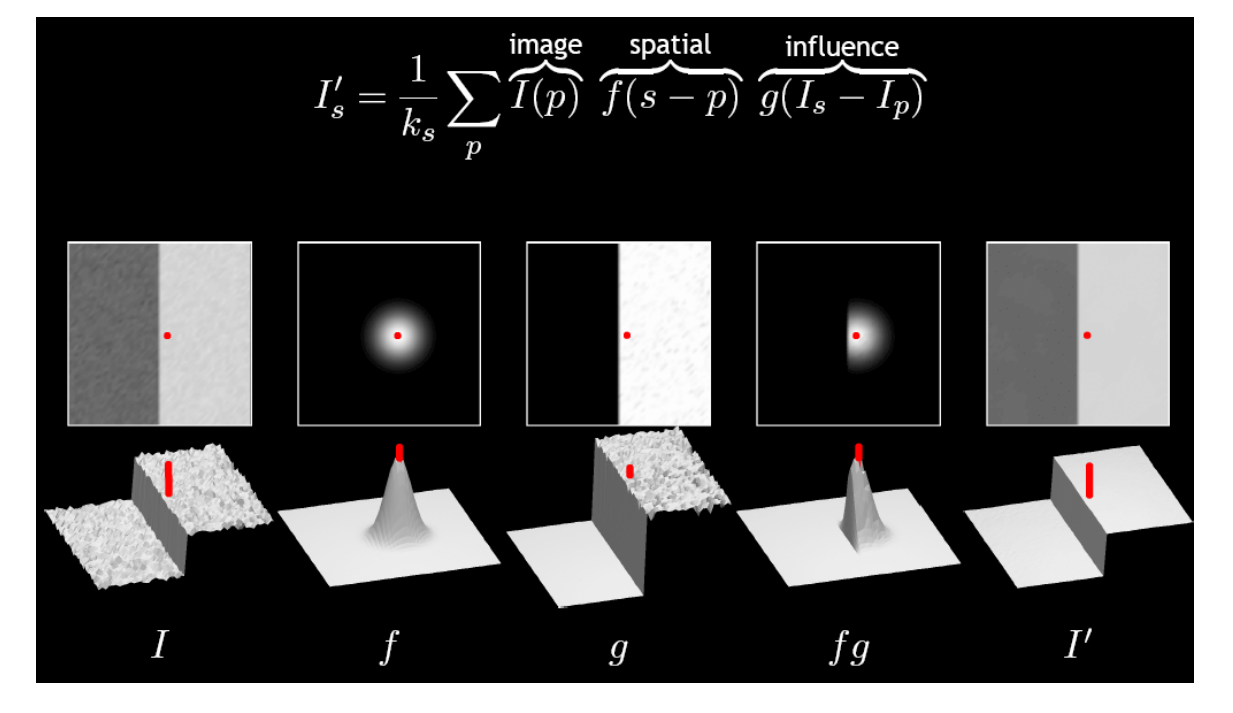
👆 f是普通的高斯权重。fg是考虑了点的距离之后的权重。
除了U和I(U),还可以根据实际情况加入更多的特征考量。
这也是人工提取特征,然后用公式表达出来的传统方法。
网格中的双边滤波

灰线:理想曲面,实际位置未知。
黄点:曲面上的点,由于带噪声呈上下分布。
蓝点:黄点中取的任意一点作为例子。
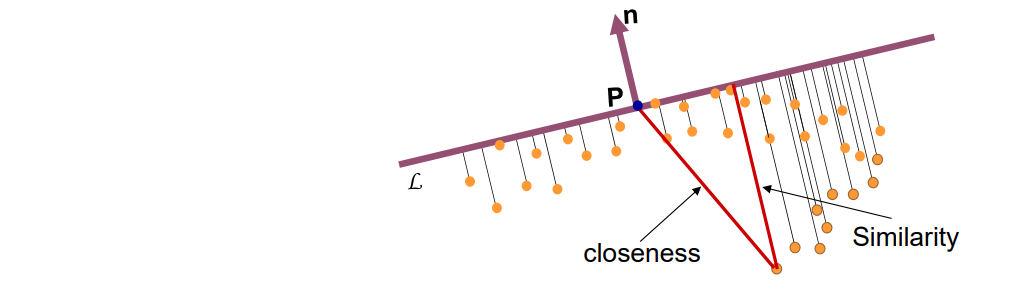
对蓝点做以下估计:
取P点邻域内的点,做PCA,最大特征值对应的向量为 P点的法向。
所有点向切平面上投影,得到距离1。
所有点向法线上投影,得到距离2。
由于同时考虑了距离1和距离2,因此称双边。
💡 我的想法:
前面提到的, feature 和 noise 很难区分。
比如例子中的棱角和噪声一样,具有高频、曲率大的特点。
但特征有连续性,在大的区间里表现出规律,而噪声不具备这个特点,可以据此区分。
效果:
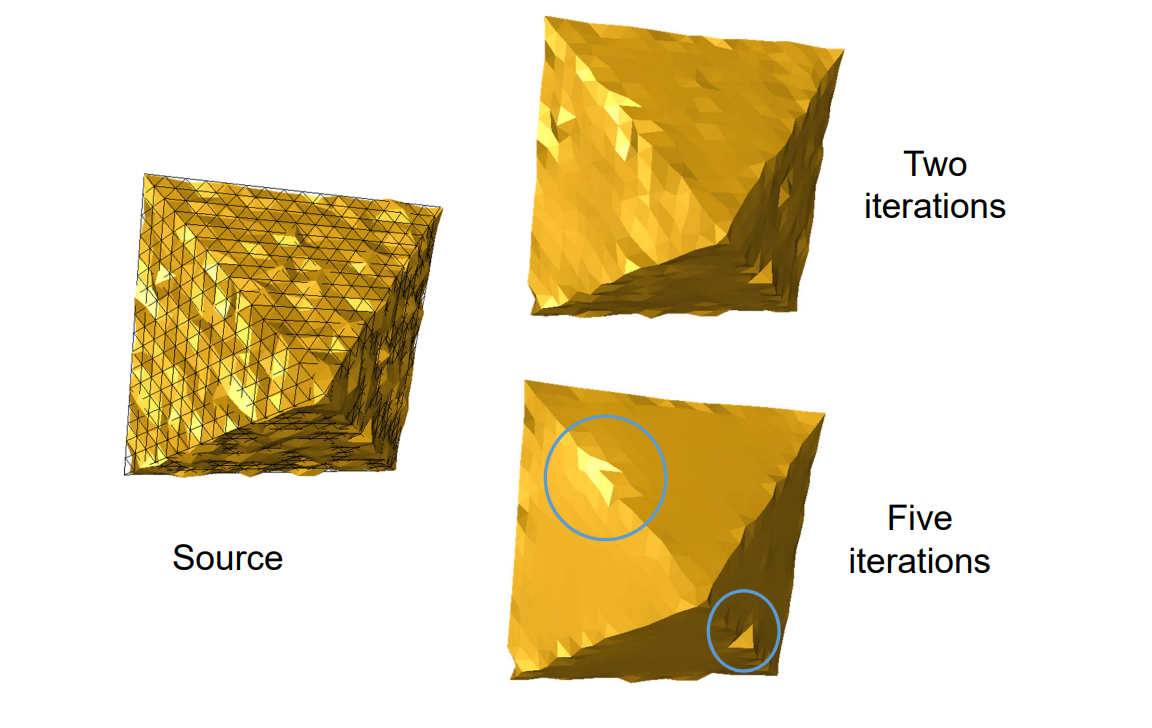
1.4 Implicit Mesh Evolutions
explicit scheme:
$$ M_{n+1}=M_n+\lambda L(M_n) $$
implicit scheme:
$$ M_{n+1}=M_n+\lambda L(M_{n+1}) \\ \Rightarrow (I-\lambda L)M_{n+1}=M_n $$
隐式方法通过求解线性稀疏方程组得到结果(类似全局法)
❓ 认为噪声是沿着法向的偏移,本身就是一种猜测、为什么说用真实曲面的法向会更好呢?
本文出自CaterpillarStudyGroup,转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/