插值型细分方法

细分方法的特点：保留原有顶点不动。对每条边，增加一个新顶点。不断迭代，生成一条曲线

可以看成是“补角法”

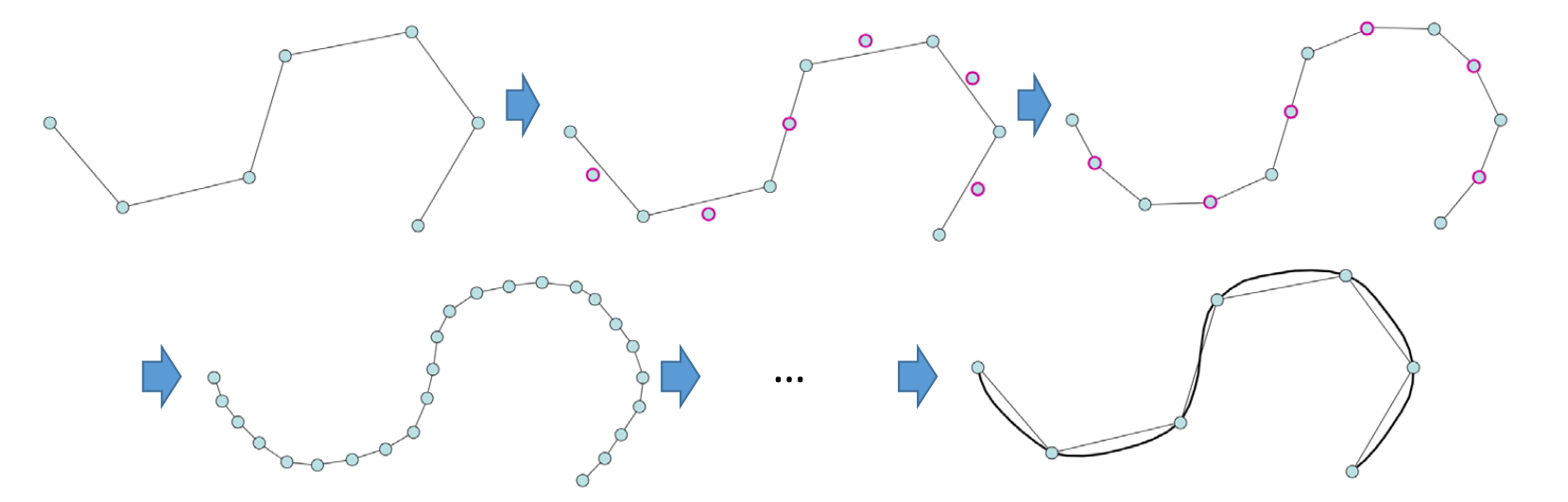
4点插值型细分

细分规则

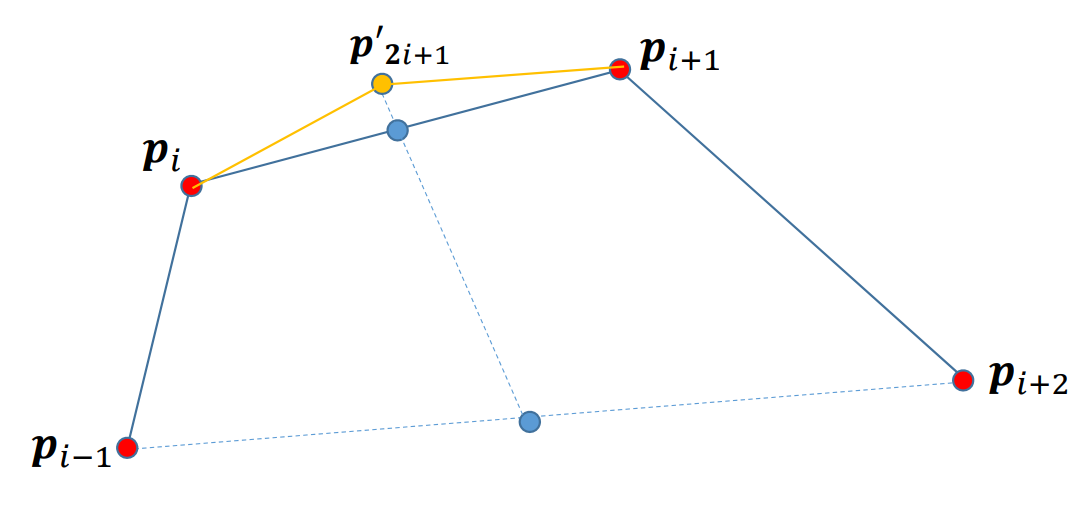
👆 蓝点分别是两条线的中点、新增点在中点连线的延长线上。

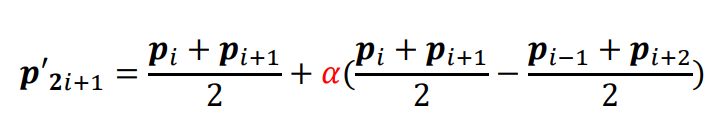
当 $𝛼∈(0,\frac{1}{8})$ 时，生成的细分曲线是光滑的；否则，细分曲线非光滑，生成了分形曲线。

🔎 Nira Dyn, David Levin, John A. Gregory A 4‐point interpolatory subdivision
scheme for curve design. Computer Aided Geometric Design, 4(4): 257‐268, 1987.

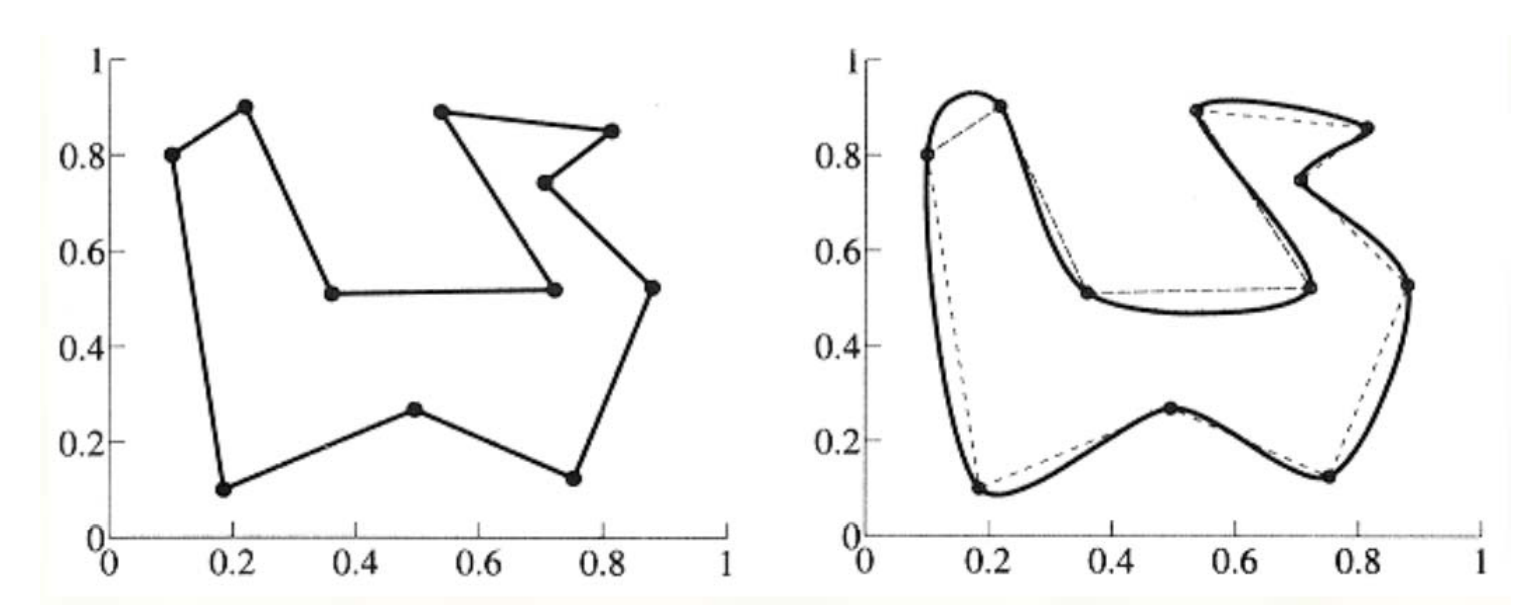
一般：2n点插值细分方法

极限曲线的连续阶随着 $n$ 增大而增加

2点插值细分方法

$P_{2i+1}^{k+1}=\frac{1}{2} (P^k_i+P^k_{i+1})$

4点插值细分方法

$P_{2i+1}^{k+1}=-\frac{1}{16} P^k_{i-1}+\frac{9}{16}P^k_{i}+\frac{9}{16}P^k_{i+1}-\frac{1}{16}P^k_{i+2}$

6点插值细分方法

$P_{2i+1}^{k+1}=\frac{3}{256} P^k_{i-2}-\frac{25}{256}P^k_{i-1}+\frac{150}{256}P^k_{i}+\frac{150}{256}P^k_{i+1}-\frac{25}{256}P^k_{i+2}+\frac{3}{256}P^k_{i+3}$

非线性细分方法

基于双圆弧插值的曲线细分方法

给定一条边,新点为插值其两端点及两端切向的双圆弧的一个连接点,也是其两端点两端切向的所确定三角形的内心.

每个细分步骤后调整切向.

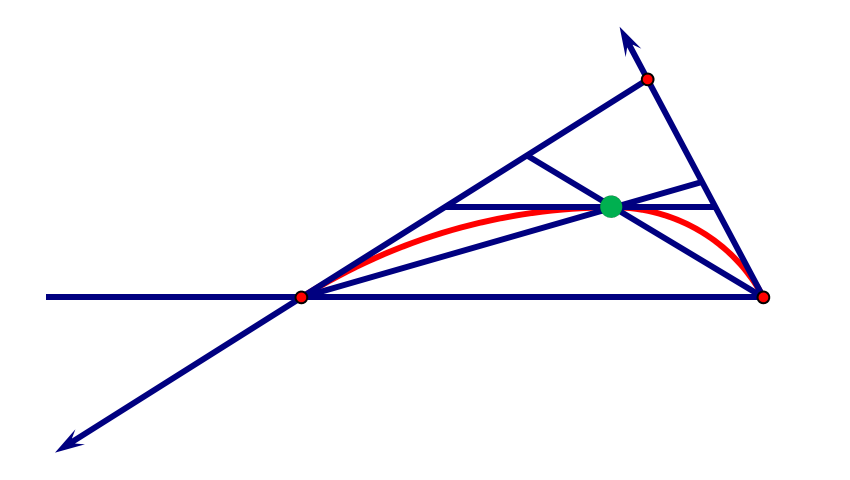
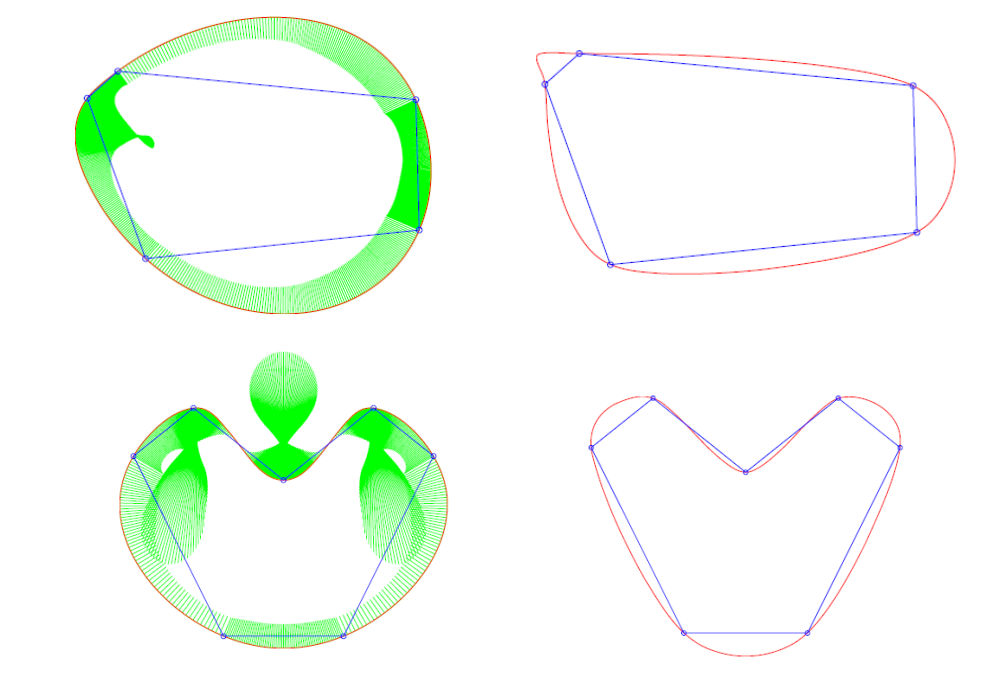
要通过解方程或优化来解

极限曲线 $𝐺^2$ ，光顺，保形

• Denis Zorin et al.Subdivision for Modeling and Animation. SIGGRAPH 2000 Course Notes
• Warren and Weimer. Subdivision Methods for Geometric Design: A Constructive Approach. Morgan-Kaufmann Publishers, 2002
• M.S. Sabin. Recent Progress in Subdivision: a Survey. Advances in Multiresolution for Geometric Modelling Mathematics and Visualization 2005, 203‐230
• Cashman. Beyond Catmull–Clark? A survey of advances in subdivision surface methods. Compute Graphics Forum, 31(1), 2012, 42–61

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/

GAMES102