构造B样条基函数： 以三次为例

1. 参数化

型值点参数，建立 $d_i 与t_i$之间的关系。

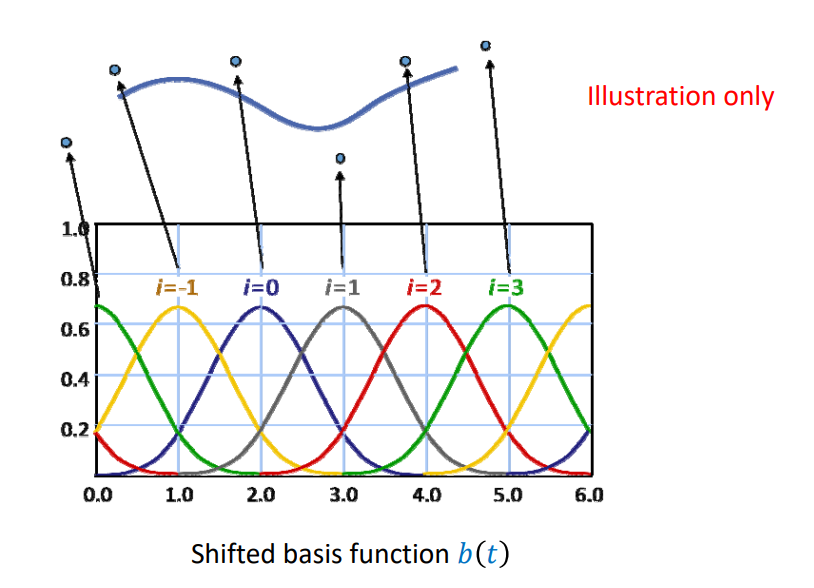
👆 图中是均匀参数化的例子。 $i$ 是参数， $i$ 的取值构成节点向量基函数通过结点向量来定义，每个基函数定义在几个特定的节点上。

2. 构造基函数𝑏(𝑡)

𝑏(𝑡)应满足以下性质

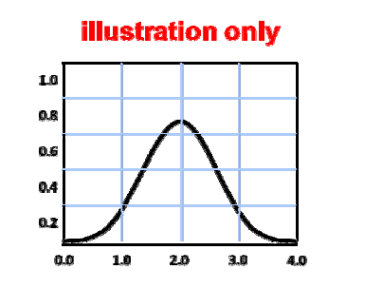
• 𝑏(𝑡) is $C^2$ continuous
• 𝑏(𝑡) is piecewise polynomial, degree 3 (cubic)
• 𝑏(𝑡) is has local support
• Overlaying shifted $𝑏 (𝑡+i)$ forms a partition of unity
• $𝑏(𝑡)\ge 0$ for all 𝑡
  In short:
• All desirable properties build into the basis
• Linear combinations will inherit these

基函数的构造方法

Repeated linear interpolation：从0阶（水平直线）开始，使用$t$和$(1-t)$进行线性组合、即升阶每升一次阶，曲线会更光滑，跨度区间会多覆盖一个结点。

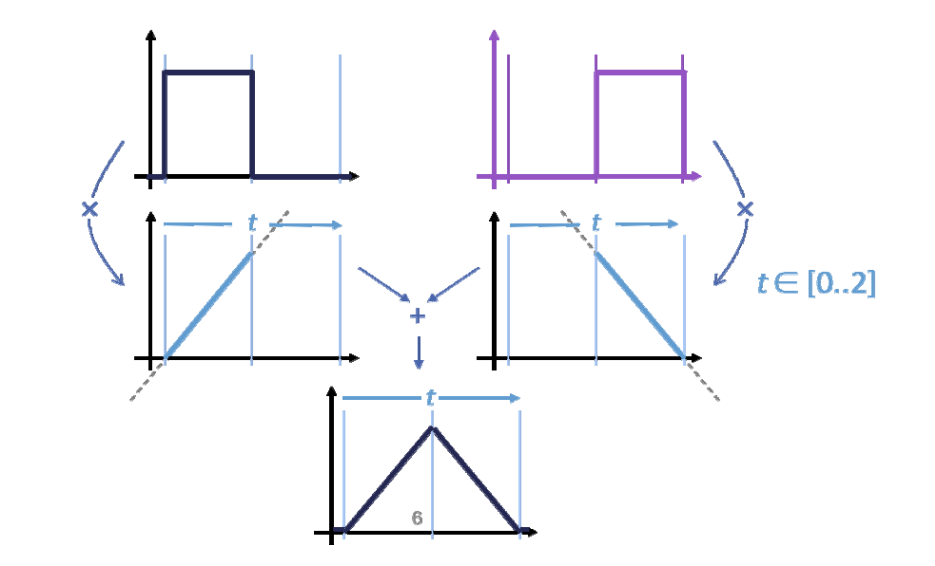
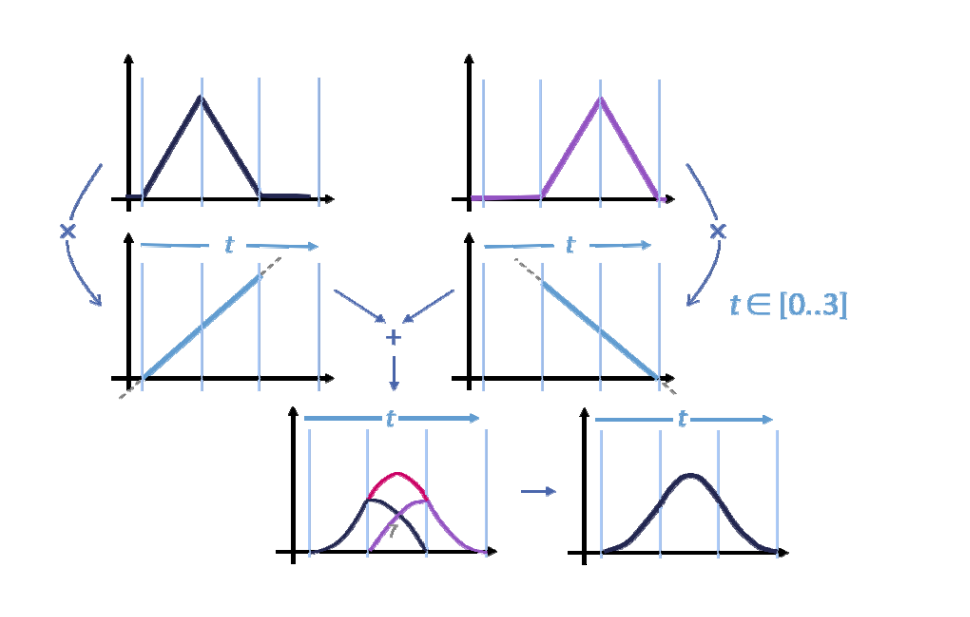
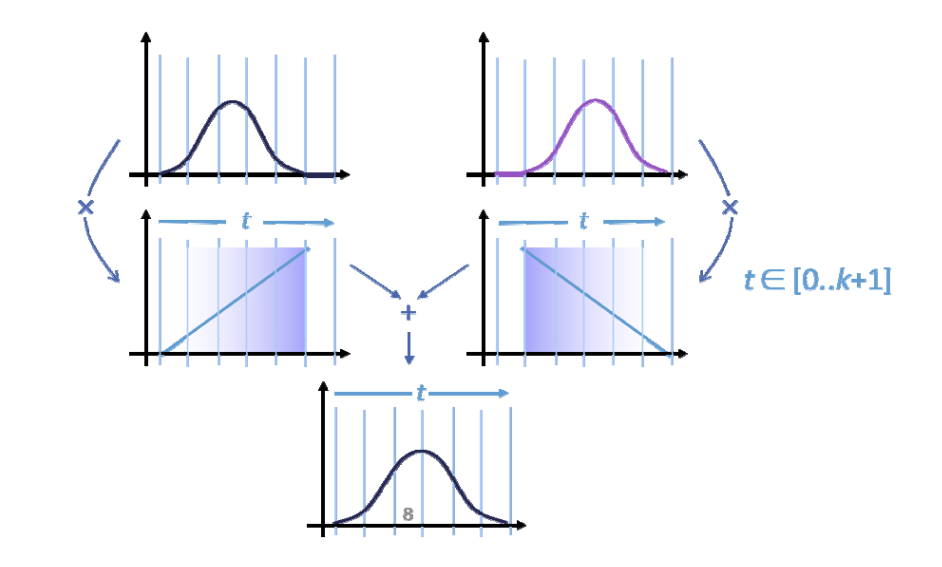
基函数的定义

De Boor Recursion: uniform k阶 B样条基函数的定义

Uniform:使用均匀参数化

B‐spline curves: general case

此页公式定义在非均匀结点上。

Given: knot sequence $t_0 < t_1 < \cdots < t_n < \cdots < t_{n+k}$ $(t_0,t_i,\cdots,t_{n=k})$ is called knot vector

Normalized B‐spline functions $N_{i,k}$of the order (degree $k-1$) are defined as:

$$N_{i,1}(t)=\begin{cases}  1,t_i\le t<t_{i+1}\\ \\ 0,otherwise \end{cases}$$

$$N_{i,1}(t)=\frac{t-t_i}{t_{i+k-1}-t_i} N_{i,k-1}(t)+\frac{t_{i+k}-t}{t_{i+k}-t_{i+1}}N_{i+1,k-1}(t)$$

for $k>1$, and $i=0,...,n$

基函数的例子

Example 1

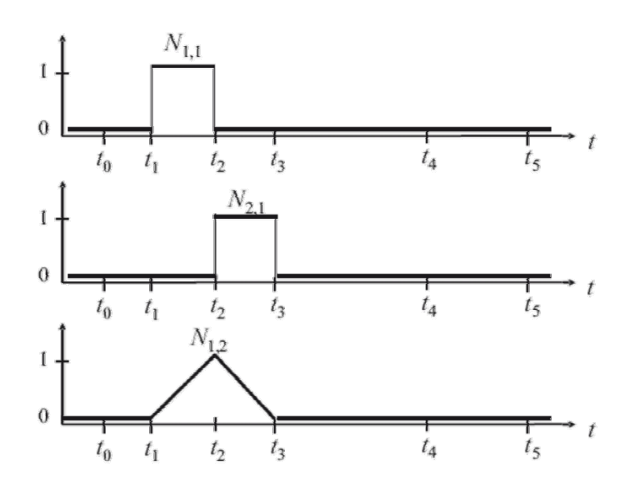
$$N_{i,1}(t)=\begin{cases}  1,t_i\le t<t_{i+1}\\ 0,otherwise \end{cases}$$

$$N_{i,1}(t)=\frac{t-t_i}{t_{i+k-1}-t_i} N_{i,k-1}(t)+\frac{t_{i+k}-t}{t_{i+k}-t_{i+1}}N_{i+1,k-1}(t)$$

for$k>1,$ and $i=0,...,n$

$N_{i, k}:K 代表阶数，i代表第i$个基函数。
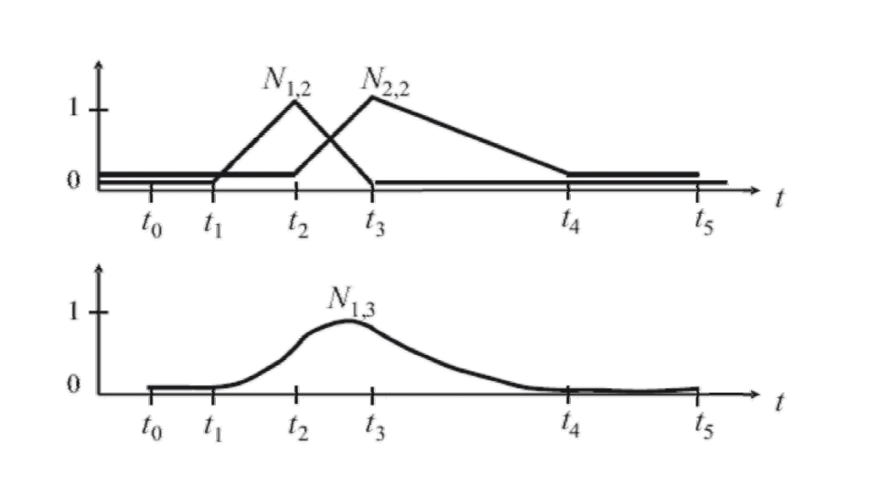
$N_{1, 1}和 N_{2, 1}组合，得到 N_{1, 2}$
$N_{1, 2}和 N_{2, 2}组合，得到 N_{1, 3}$

Example 2

Example 3

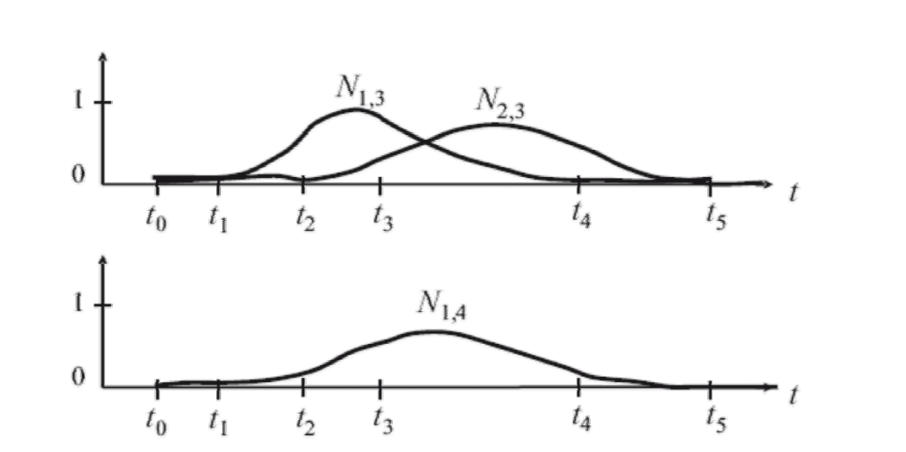
3. 基函数的平移和伸缩

每个基函数是同一个基函数的平移或伸缩得到，其中第 $i$ 个基函数是以$t_i$为中心的局部函数。

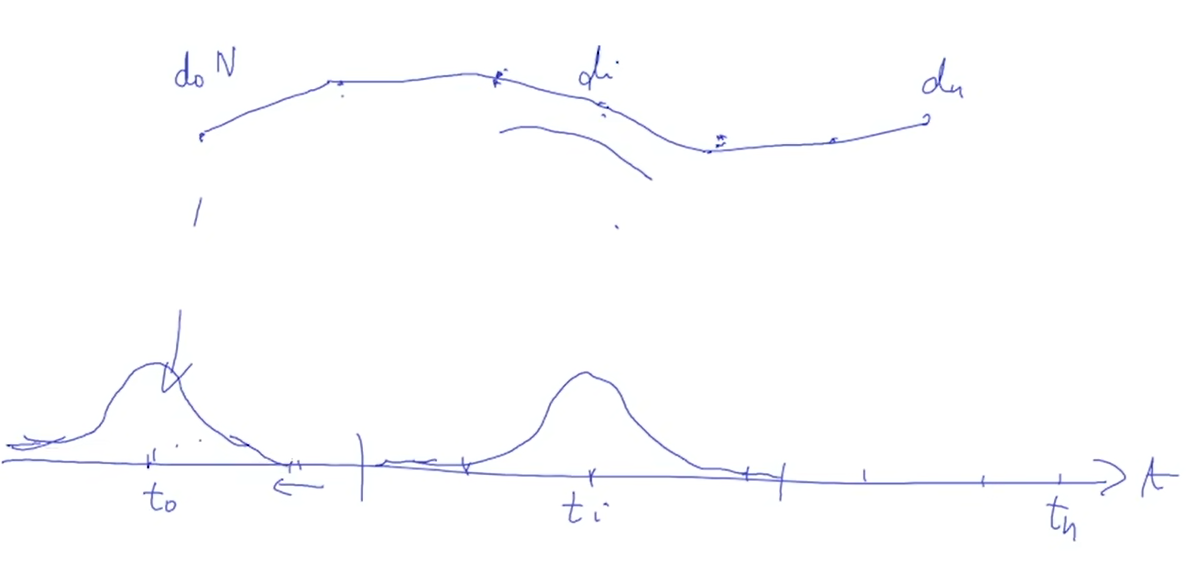
基函数性质

局部性

$𝑁_{i,k}(t)$ > 0 for $𝑡_i < 𝑡 < t_{i+k}$
$𝑁_{i,k}(t)$ = 0 for $𝑡_0 < 𝑡 < t_i$ or $t_{i+k} <t < t_{n+k}$

The interval $[t_i,t_{i+k}]$, is called support of $N_{i,k}$

权性 + 凸包性

$\sum_{i=0}^{n} N_{i,k}(t)=1$for $t_{k-1}\le t\le t_{n+1}$

光滑性

For $\quad t_i\le t_j\le t_{i+k}$, the basis functions $N_{i,k}(t)$ are $C^{k-2}$ at the knots $t_j$

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/