从曲线的曲率图的直观理解
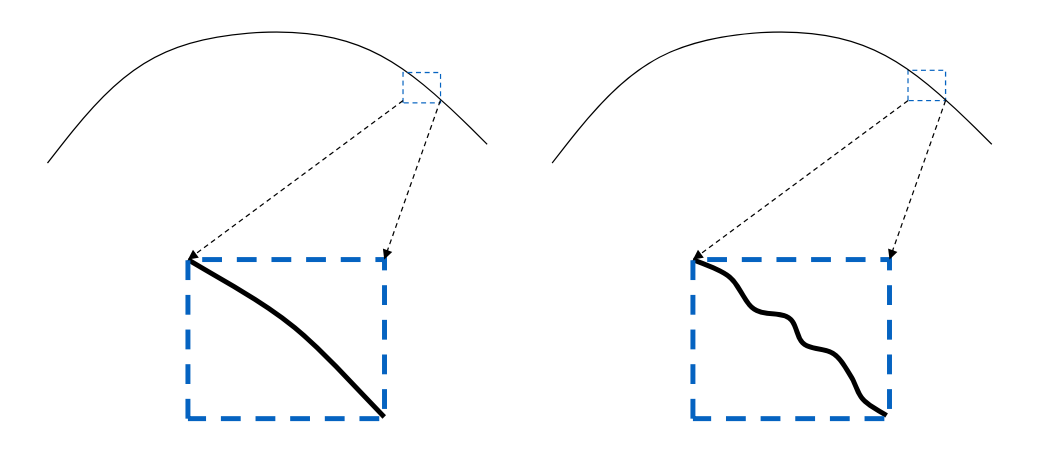
看上去光滑的曲线,放大后发现是凹凹凸凸的(右)
Fairing Design is Important!
• Shoe sole
• Cam profile
• Ship hull:船的表面光顺可以减小水的阻力。
• Car profile
• Plane profile
• …
光顺的定义
为什么光顺难以定义
光顺是一种微观的性质,很难描述
是否光顺取决于人的主观和经验
没有明确的数学定义
没有客观的测量方法
光顺的参考定义
- [Su and Liu 1978]
- \(C^2\) continuous
- curvature plot is free of any unnecessary variation
例如: the distribution of curvature must be as uniform as possible.
- [Farin and Sapidis, 1989]
- curvature plot consists of relatively few 单调段(monotone pieces)
- [Farin 2002]
- curvature plot is continuous
- curvature plot consists of only a few monotone pieces.
- [Roulier and Rando, 1994]
- \(C^2\) continuous
- minimizes the integral of the squared curvature with respect to arc length
$$ \int _ck^2ds=MIN $$
这是用整条曲线的能量来定义,是全局面定义法。
Observations of Fairness
- Neither a global problem nor a local problem, but a large local problem
• Not an energy minimization problem - Need not \(C^2\) continuous
• Circular spline - Intimately related to uniform distribution of curvature
• Curvature is a “magnifier” of the curve fairness
不能用\(\int K^2=MIN\) 来定义,有可能k不大,但频繁挠 动,仍不算光顺。
Example 1
$$ y=\sin x, x\in[0,6\pi] $$

The curve is \(C^\infty \),但并不光顺
原因:拐点(vibration)数太多
拐点即 from convex to concave or from concave to convex
Example 2
$$ y=\frac{1+\delta }{0} x^2+\sin x,x\in [0,6\pi ],\delta >0 $$
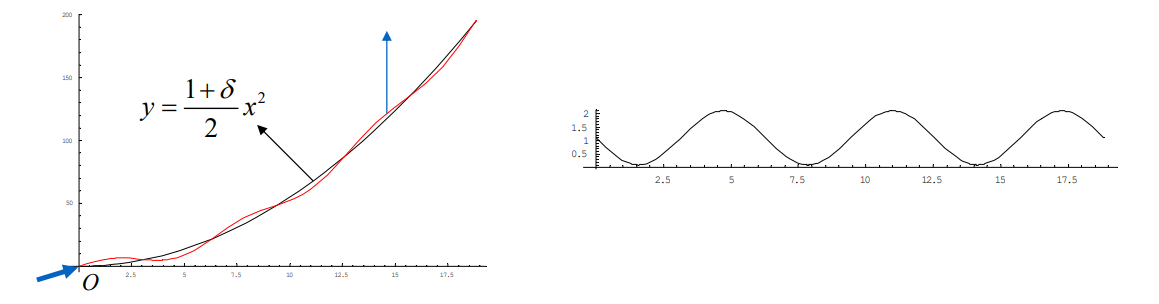
$$ {y}'' =1+\delta -\sin x > 0 $$
The curve is \(C^\infty \)且一直在递增无拐点,但仍不光顺
原因:\(y''\)有太多振荡。
Example 3
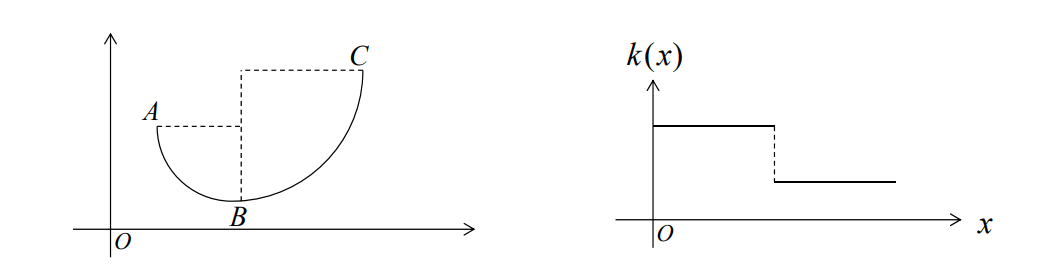
The curvature function \({y}''(x) \)不满足G2连续。
\(k_1\)与\(k_2\)变化不大时光顺。
原因:\({y}''(x) \) has large amplitude at discontinuity point.
不满足\(C^2\)连续,但光顺,因此\(C^2\)不是必须的。
曲线的光顺的“新定义”
一条曲线是光顺的,如果
(1)它是\(C^{l+1} ( l > 0 )\)连续的;
(2)它的曲线本身拐点较少;
(3)它的曲率图的拐点较少;
(4)它的曲率图变化的振幅相对小。
说明 1: 条件(1)中的 \(C^{1+l}\) 是要求曲线为 \(C^{1}\) 连续而不必\(C^{2}\),但\(C^{1}\)的导数满足有界变差。条件 (4) 则要求曲线在曲安非连续点处的跳跃要尺尽可能小。
说明 2: 满足 (2)和(3)描述的曲线的它的曲率图含有的单调段都会相对少。这与前面所述的判 别准则 1-4 一致。
💡 光顺很难定义,为什么一定要给它一个定义?因为定义代表了一个明确的标准,在同一个标准下讨论问题才有意义。
Remarks
震荡数 Vibration:Change from convex to concave or change from concave to convex
一阶震荡数 First vibration number \(R\):Vibration number of \(y(x)\)
二阶震荡数 Second vibration number \(S\):Vibration number of curvature function
本文出自CaterpillarStudyGroup,转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/