回顾

曲面参数化
映射（ Mapping / Map ）
平面几何映射

映射的表达

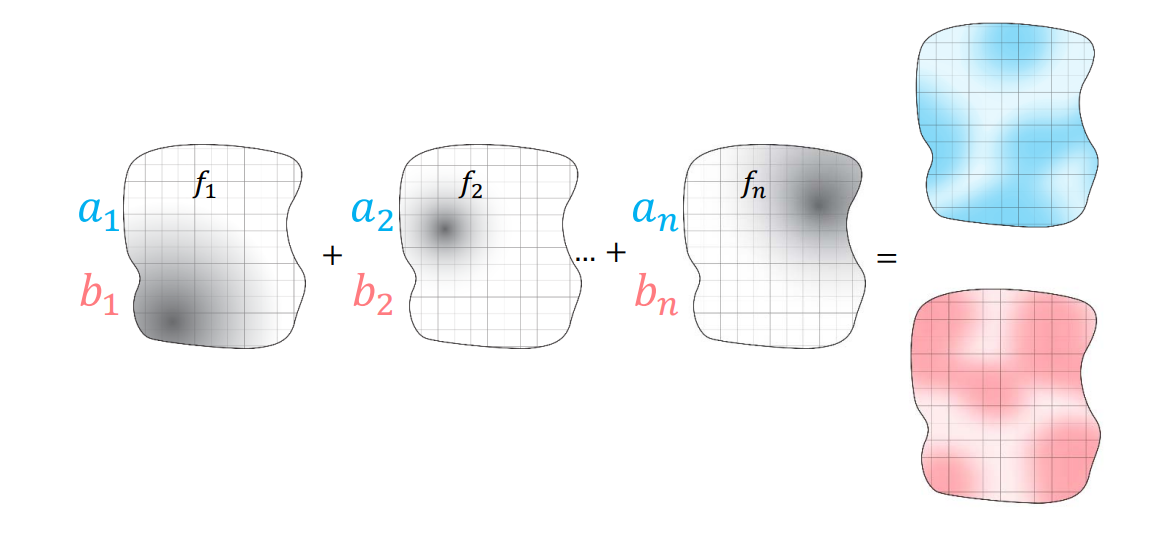
映射：基函数的线性组合

映射表达为基本映射（基函数）的线性组合

• 基函数(basis functions):

$$f_1,f_2,f_3,\cdots ,f_n$$

• 基函数的线性组合：

$$f(X)=\begin{pmatrix}u(X) \\v(X) \end{pmatrix}=\begin{pmatrix}\sum a_if_i(X) \\\sum b_if_i(X) \end{pmatrix}$$

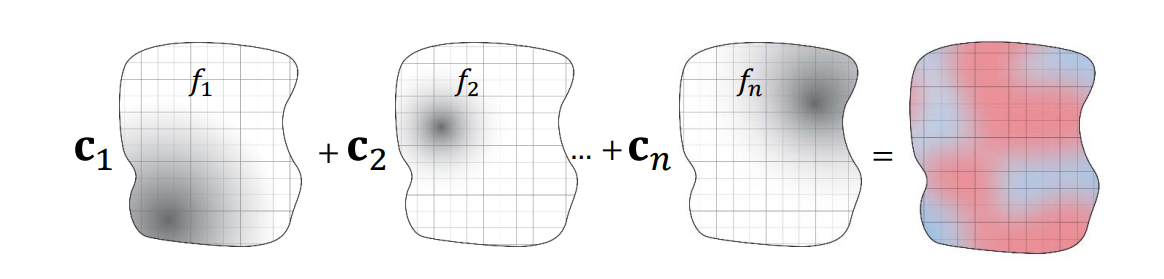
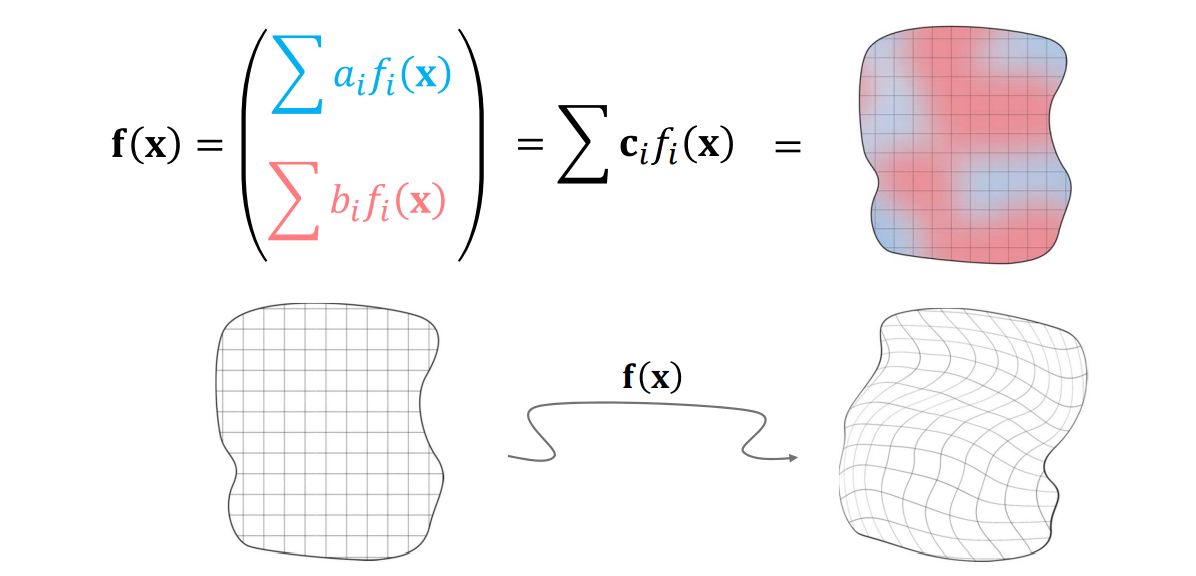
映射：简单区域上映射的连续组合

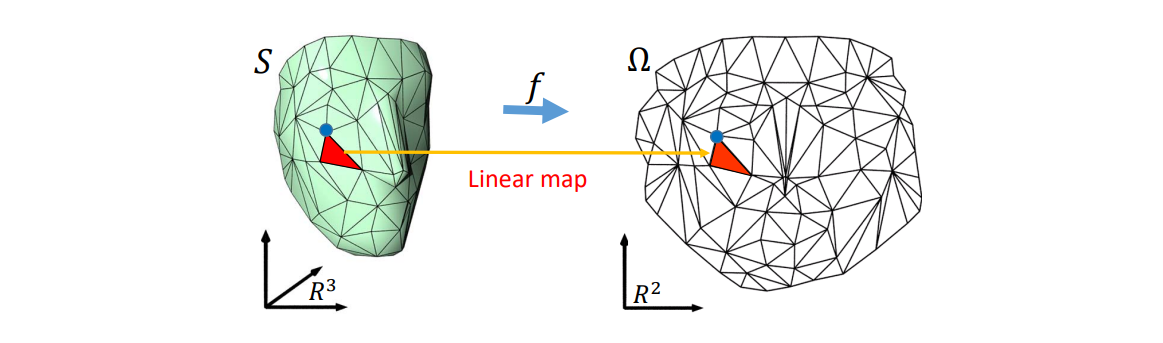
映射表达为小区域（三角形区域）上映射的拼接

$f$ is approximated by piecewise linear maps between pairs of triangles

几何映射的例子

例1：2D变形

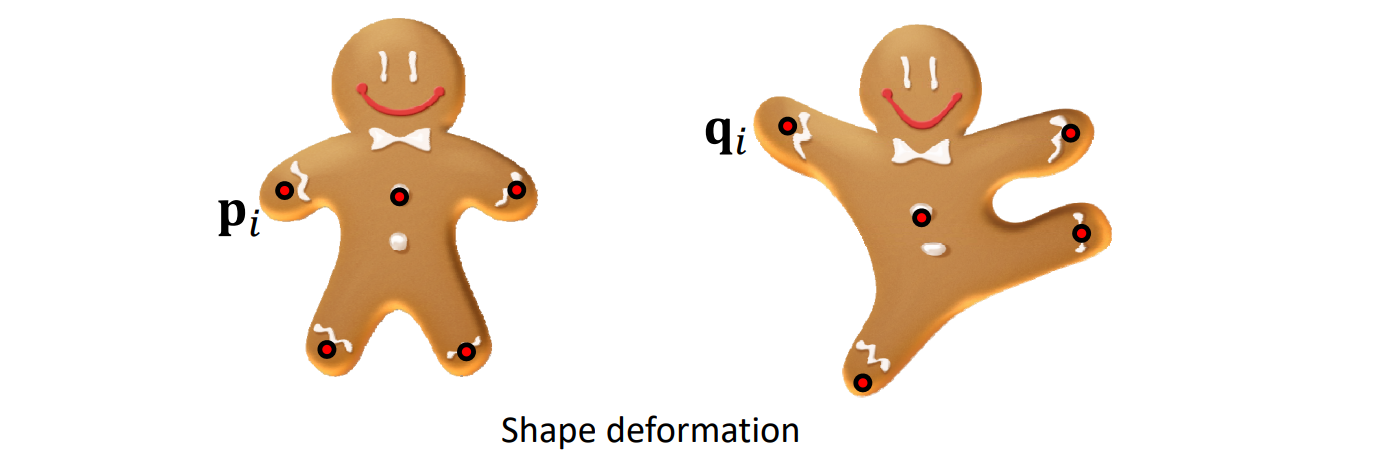
[06:51] 2D变形问题：构造一个函数$f$， 使得拖拽点$f(P)$满足到达目标点的约束。
[10:06] 或$f(P)$满足$f'(P)$为目标值的约束，就是法线插值。
[10:43] mesh 点是指定点（例如重心坐标）的组合。通过移动指定点控制mesh.

本质：插值问题

例2: Barycentric Coordinates

重心坐标：link

映射的性质

问：What are good maps?

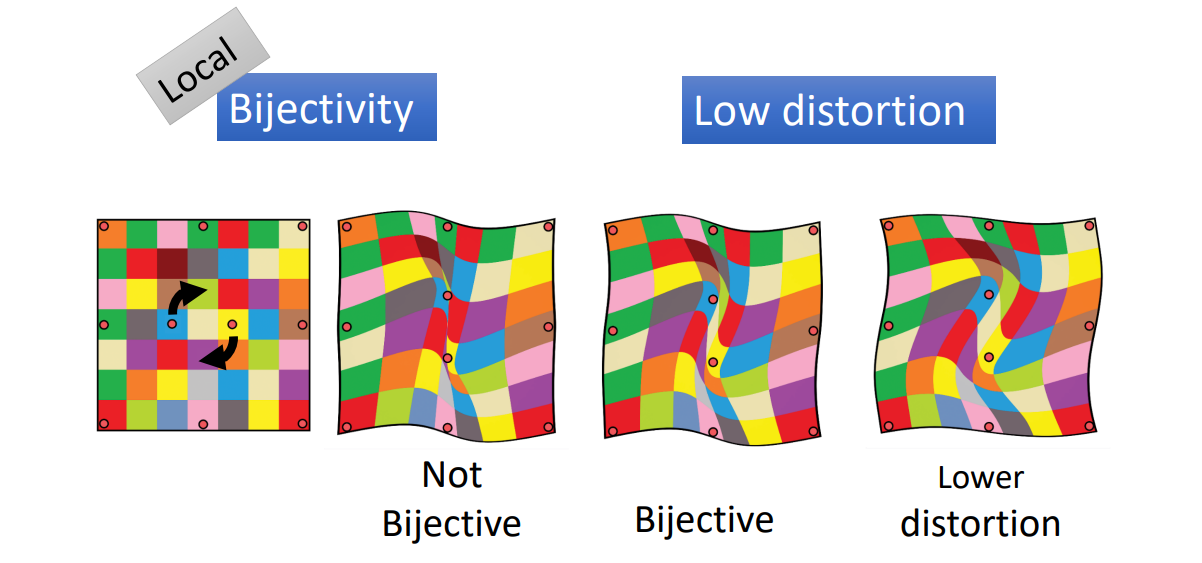
答：（1）满足双射，即Source 与 target 一一 对应。local 双射（单射)：一一对应，但有翻转发生
（2）扭曲尽量少，否则有鬼影现象 [21:28下图]

翻转 Flip (foldover) - 单射

现象

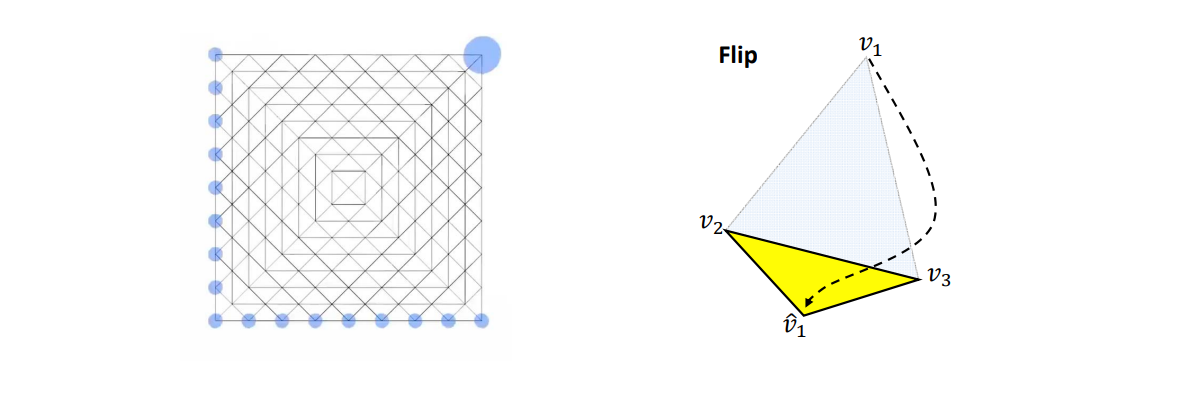
原理

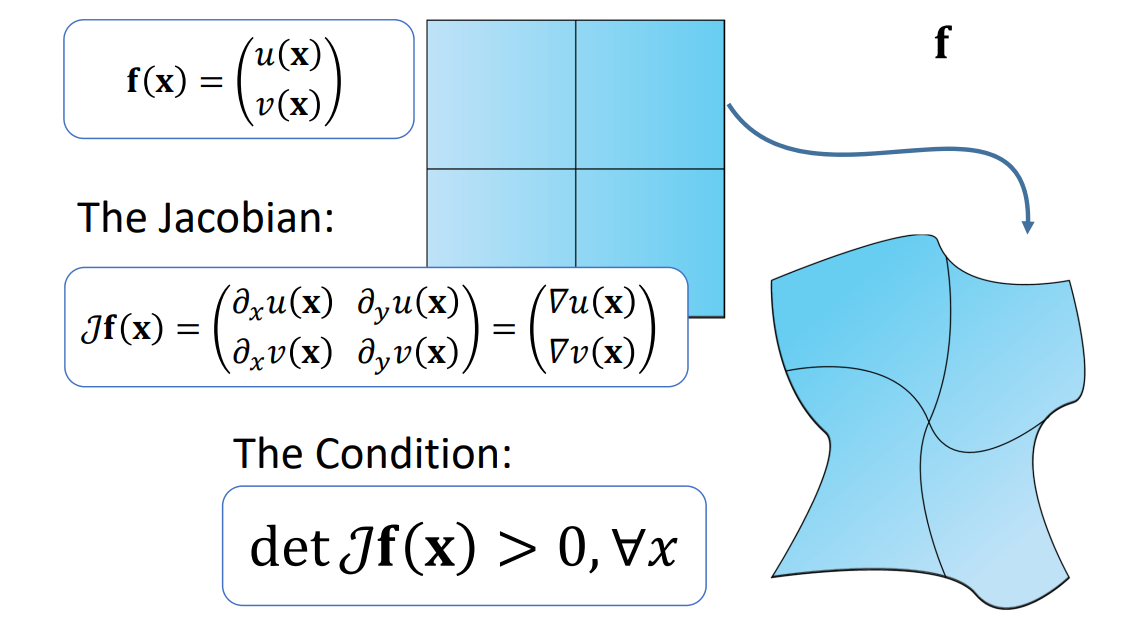
$f(x)$是映射关系，求$f$的 Jacobian,

$J$是每个分量分别对$x$和构成偏导
$\det|J| >0 \Rightarrow$未翻转。

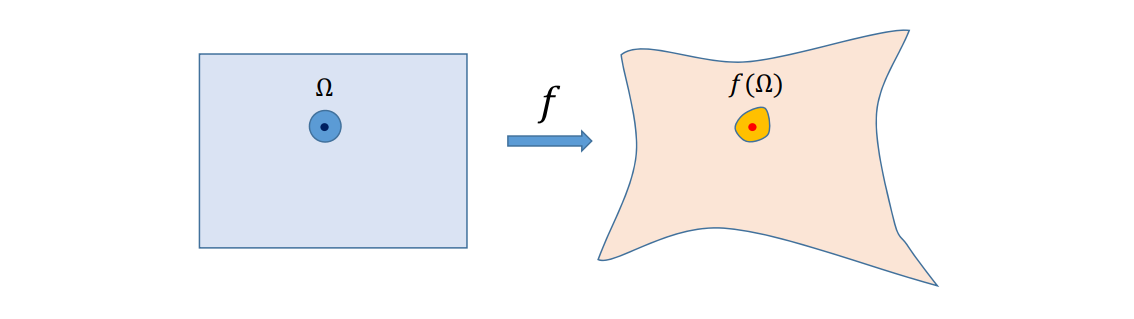
[图23:35]有两个区域 $D_1, D_2$,
$\Omega$ 为$x_0$的无穷小邻域
$\Omega$映射到$D_2$后成为$f(\Omega)$
A: signed area. $$y=\underset{A(\Omega )} {lim}=\frac{A(f(\Omega ))}{A(\Omega )} =J(f)l_{x=x_0}$$ |y|>1：膨胀
|y|<1:收缩
y<0：翻转

[31:02] 3D空间则分解为$\sigma _1,\sigma _2,\sigma _3$
[32:02图] 有一个矩形，希望把它边界变成红线形，求变形后的形状：
期望：形变较小/夹角小$\dots$ (看应用需求)

Globally Bijective - 双射

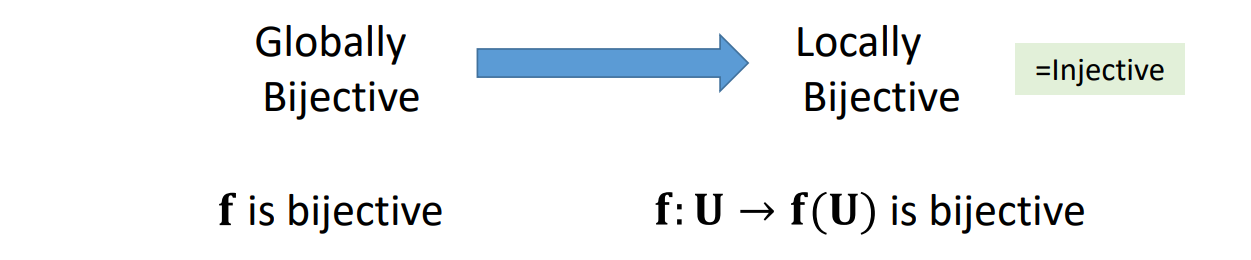
单射→双射：需要显式地判断是否发生碰撞

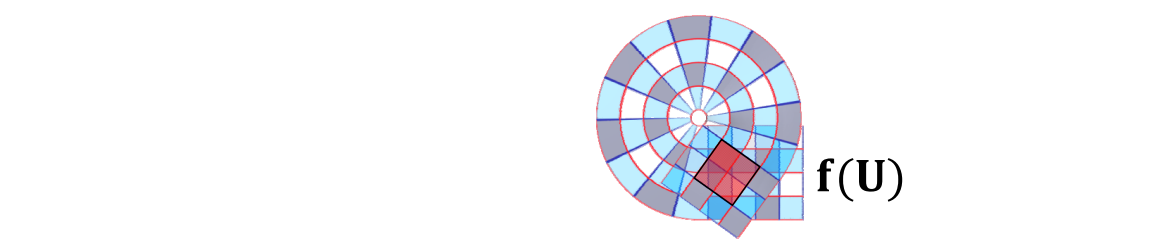
这里的形变，虽然每个面片都没有发生翻转，但整体上发生了碰撞，不满足双射

扭曲

Jacobian的几何意义

函数在某点的Jacobian度量了其局部的形变量

$$L=U\begin{pmatrix} \sigma _1 & 0\\ 0 &\sigma _2 \end{pmatrix}V^*$$

$$\sigma _2\ge \sigma _1$$

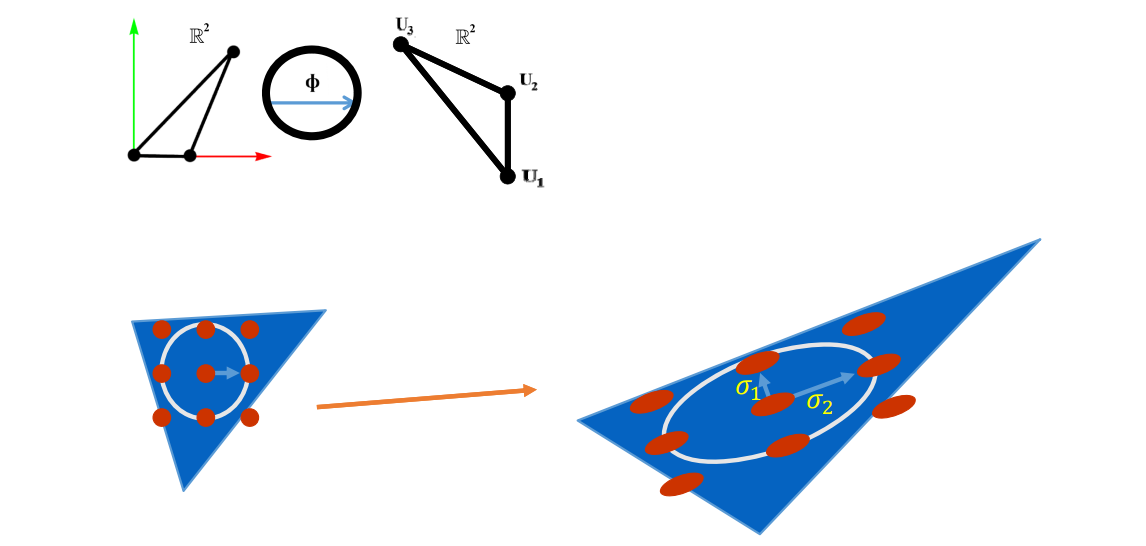
• angle‐preserving (conformal) $\sigma _1= \sigma _2$

• area‐preserving (authalic) $\sigma _1\sigma _2=1$

• length‐preserving (isometric) $\sigma _1=\sigma _2=1$

其它Distortion Metric

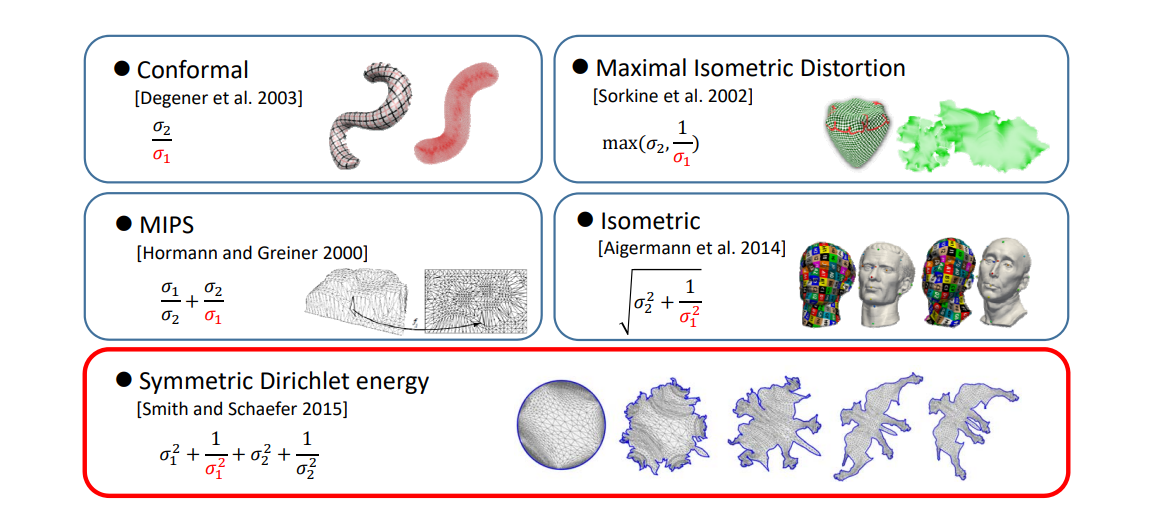
映射的优化模型

Recap: Formulation of Parameterization

$$\min_{V} E(V)=\sum _{t\in T}(\sigma _1^2+\frac{1}{\sigma _1^2} +\sigma _2^2+\frac{1}{\sigma _2^2})$$

$$s.t.\sigma _1\sigma _2>0,\forall t$$

• The cost function is highly nonlinear and nonconvex
• The constraints are nonlinear
• The Heissian matrix is highly non‐definite

Computationally expensive for large scale meshes!

要解决的问题

输入：

可能的输出：

希望找到形变较少的度量，不同的度量会得到不同的结果

优化的能量

基于不同的度量，生成对应能量函数，进行优化

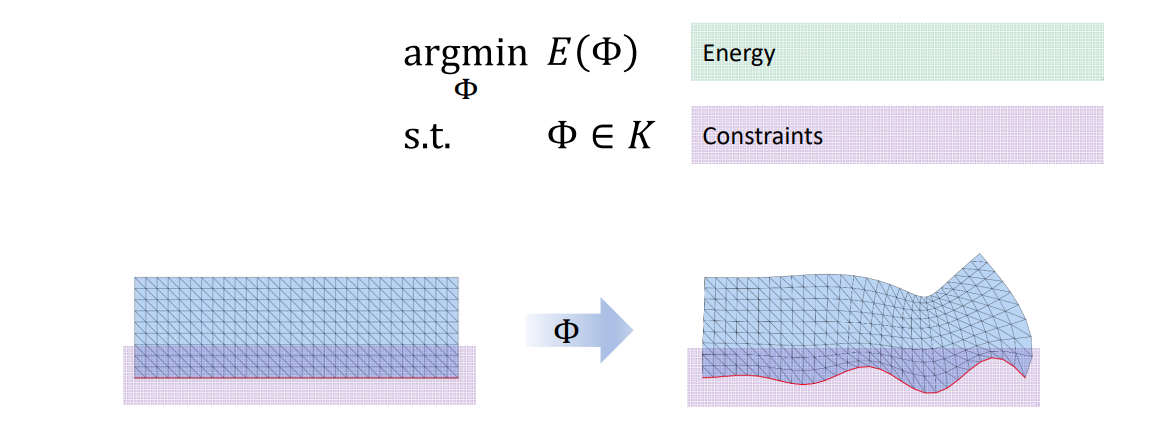
能量由每个三角形的变形能量相加得到：

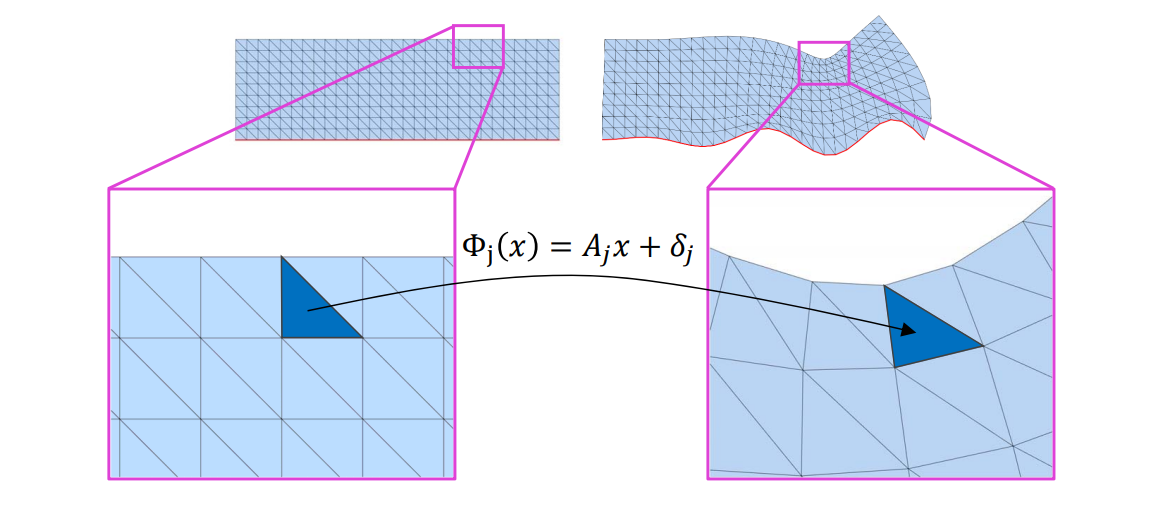
$$E(\phi )=E(A_1,\cdots ,A_m) = \sum _jf(A_j)$$

Map optimization

同时要考虑三角形能够拼到一起。

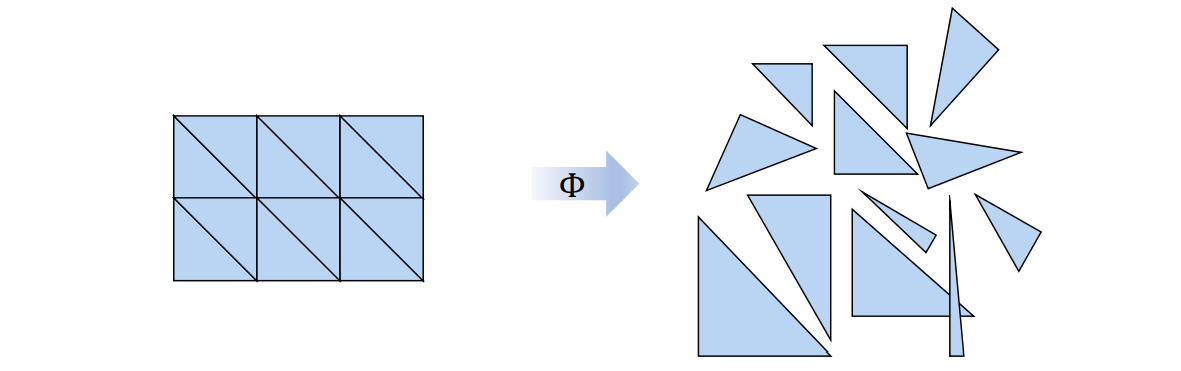
Explicit continuity

优化参数: $A_1,A_2,\cdots ,A_m$
相邻三角形的$A$应满足约束：

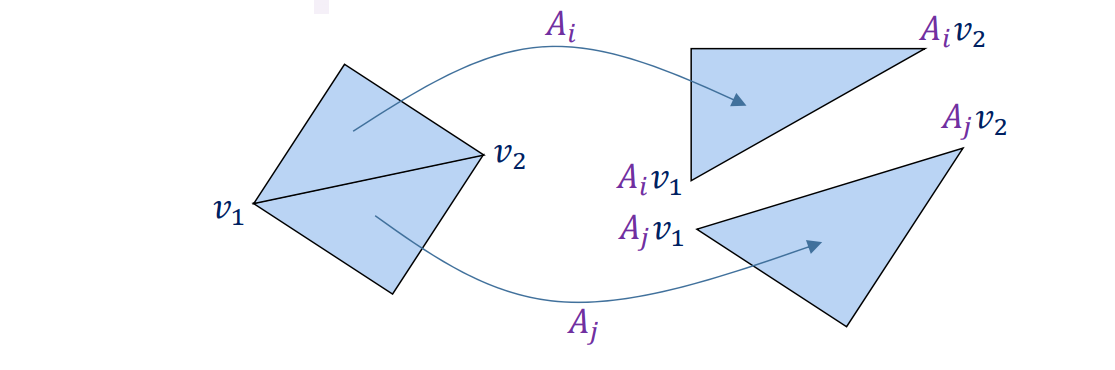
$$A_iv_1=A_jv_1$$

$$A_iv_2=A_jv_2$$

Implicit continuity

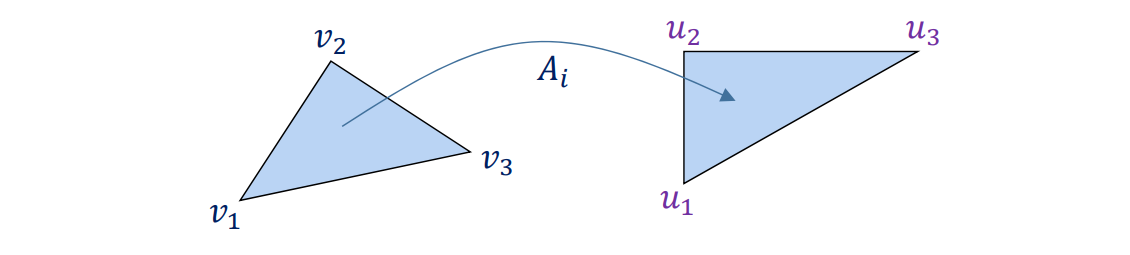
$$A_i\overline{\begin{bmatrix} \nu_1 & \nu_2 &\nu_3 \end{bmatrix}} =\overline{\begin{bmatrix} u_1 & u_2 &u_3 \end{bmatrix}}$$

$$A_i=\overline{\begin{bmatrix} u_1 & u_2 &u_3 \end{bmatrix}} \overline{\begin{bmatrix} \nu_1 & \nu_2 &\nu_3 \end{bmatrix}}$$

$$A_i=A_i(U)$$

变量不是$A$，而是$u$，$A$是由$u$决定的

Optimization variables: $u_1,u_2,\cdots ,u_n(U)$

$$E(\Phi )=\sum _jf(A_j(U))$$

这种方法更常用

几何优化的求解

优化能量，关键是怎么定义能量

各种能量

Dirichlet能量

area / volume $\Rightarrow E_D=\sum _jw_j||A_j||_F^2$

公式没有几何意义，纯粹是一种度量。
会造成比较大的扭曲，现在很少用了

Orthogonal and Similarity

• R is orthogonal if $R^T=R^{-1}$
(rotation if det 𝑅 > 0)

• S is a similarity if $S =\alpha R$

• $\Re(A)=$ closest orthogonal/rotation matrix to $A$
• $\varsigma (A)$= closest similarity matrix to $A$

对A做SVD/SSVD分解:

$A=U\sum V^T$;$\sum$ =diag$(\sigma _1,\cdots ,\sigma _n)$

As‐Similar‐As‐Possible (ASAP)

$$E_L=\sum _jw_j||A_j-\varsigma (A_j)||_F^2$$

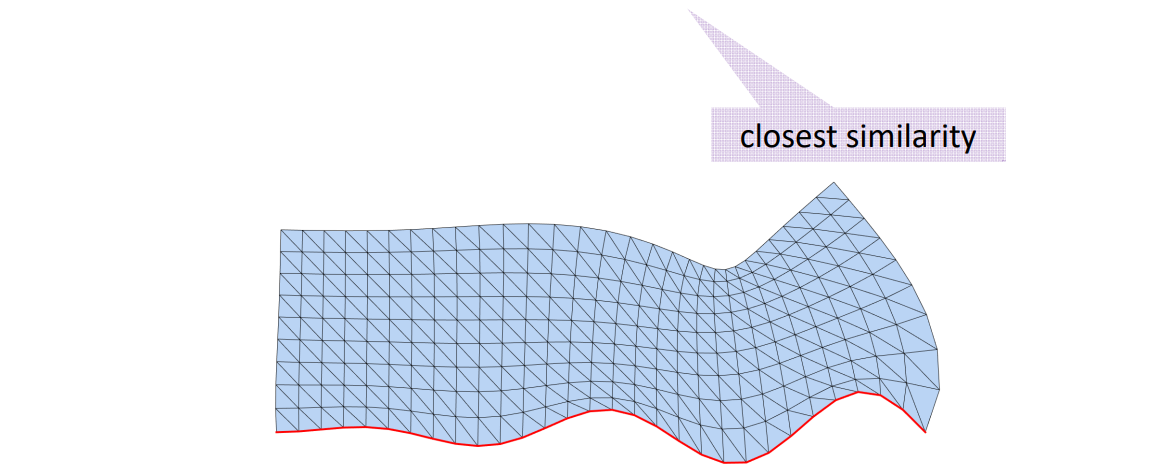
Solving sparse linear system!

As‐Rigid‐As‐Possible (ARAP)

$$E_R=\sum _jw_j||A_j-\Re (A_j)||_F^2$$

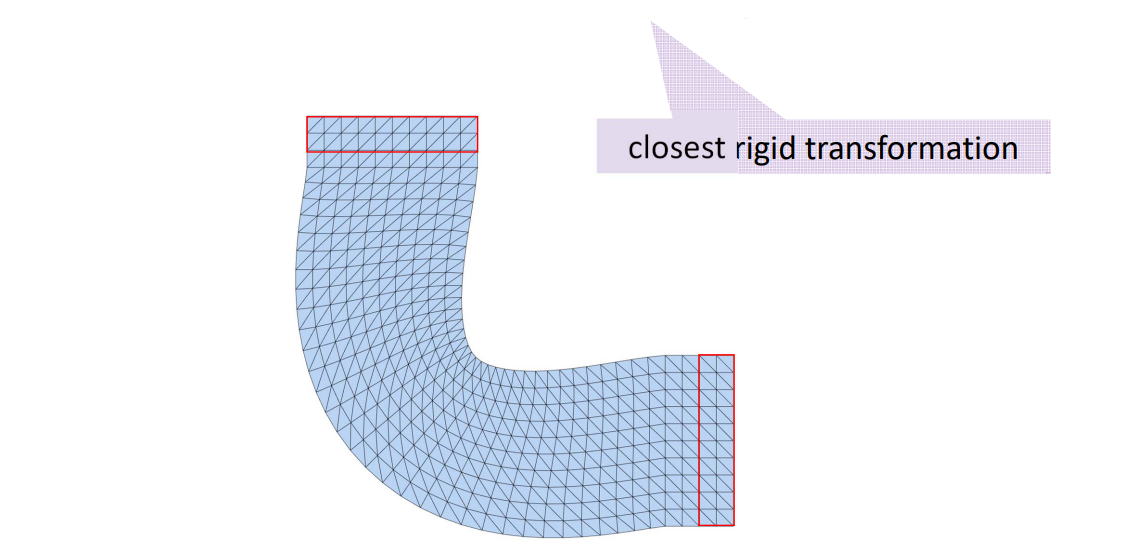
Alternating Optimization

• Iteratively:
  • Compute and fix $R_j = \Re (A_j)$ Local step

• Minimize

$\sum _jw_j||A_j-R_j||_F^2$ Global step

[Liu et al. A Local/Global Approach to Mesh Parameterization. SGP 2008]

[42:11] locd: 分裂 global:缝合
交替迭代优化方法

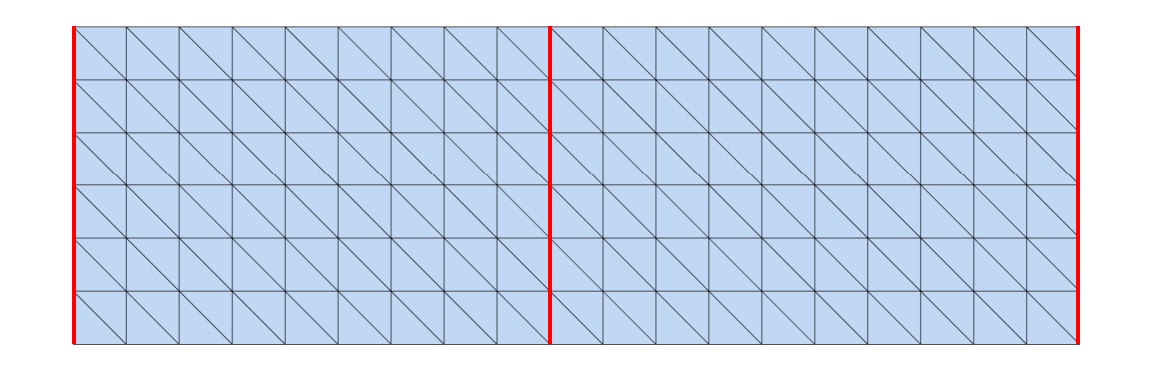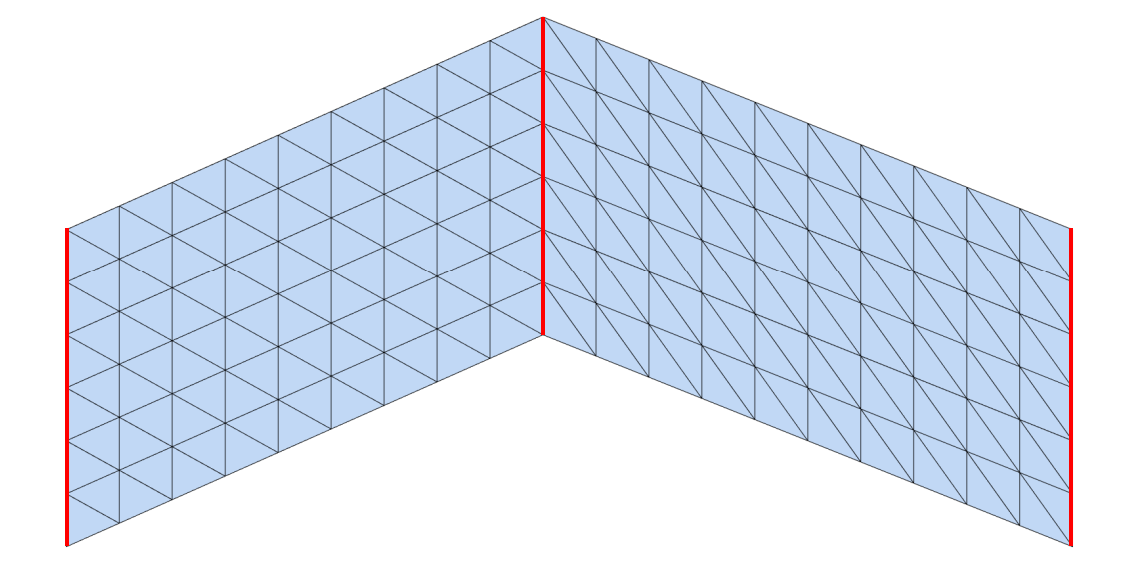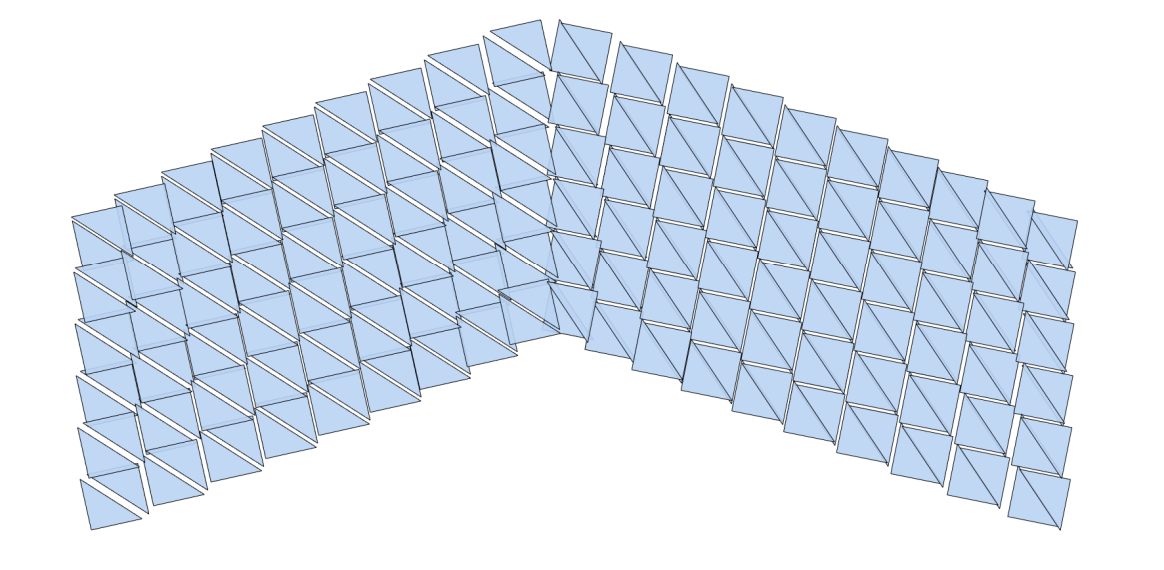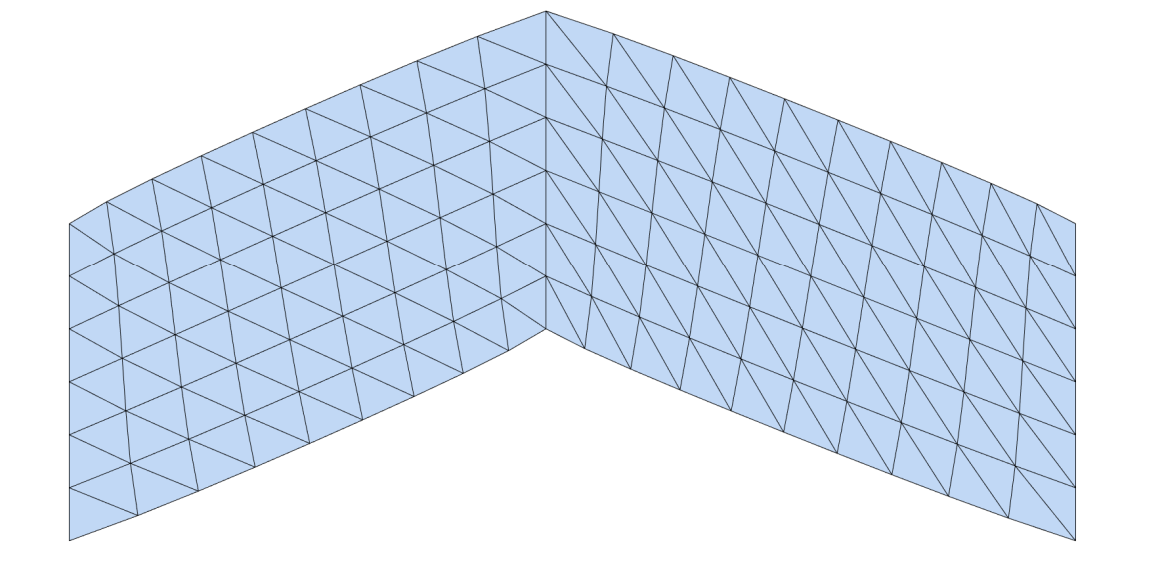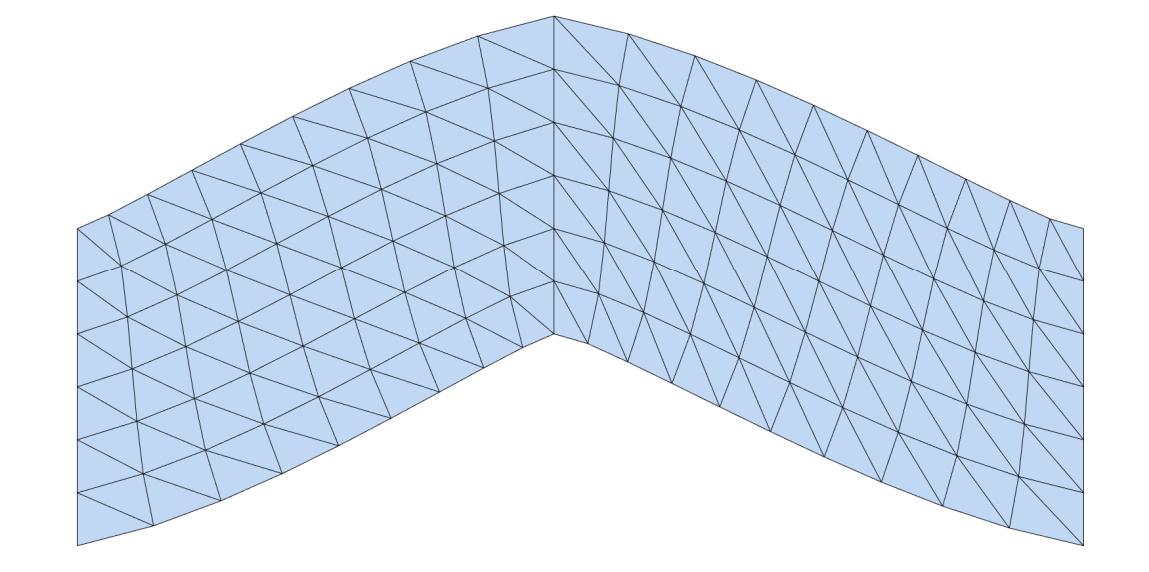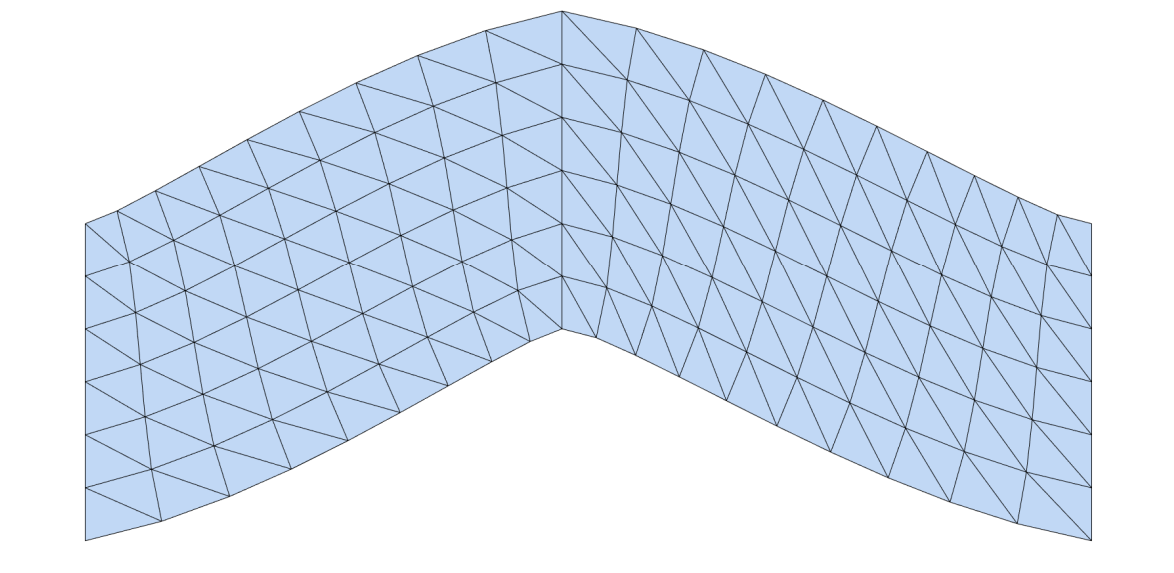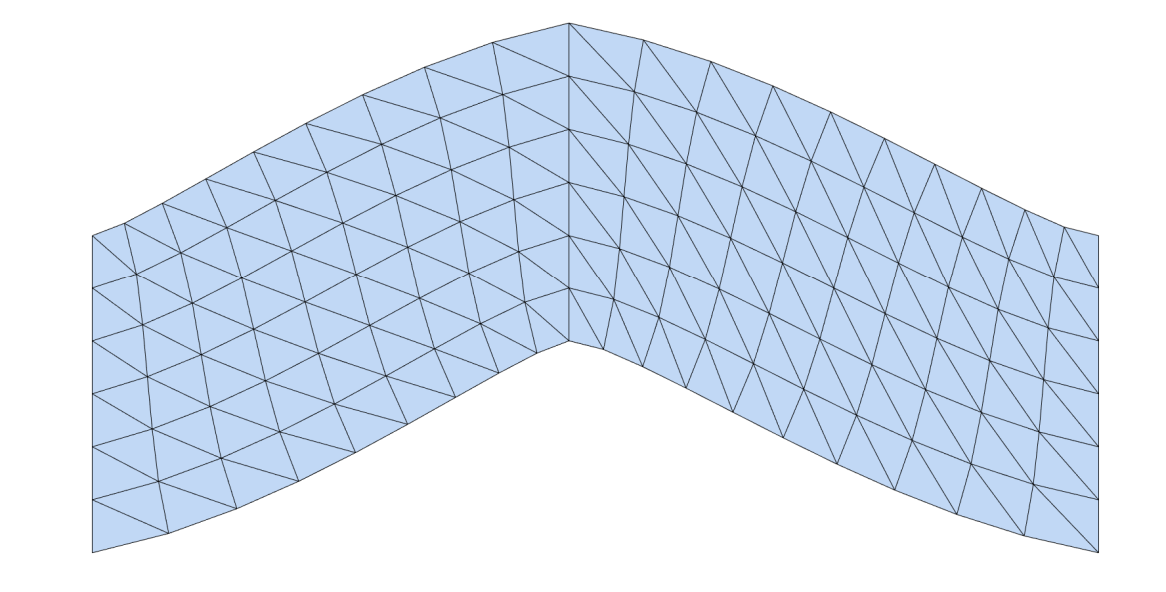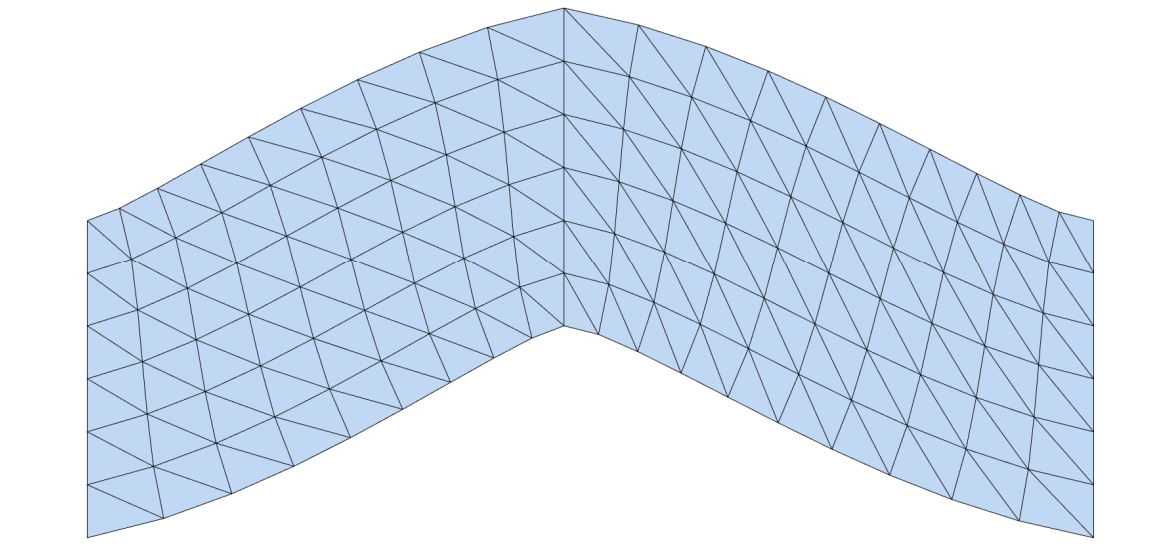交替优先的方法非常常用

各种方法的比较

ARAP vs. ASAP

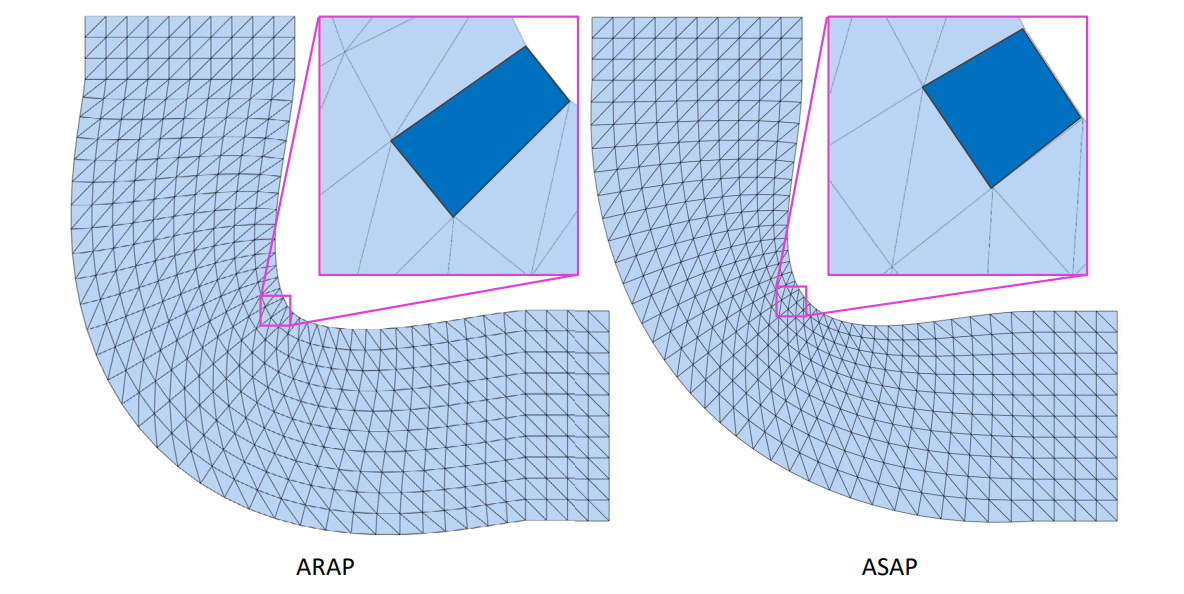
Singular values perspective

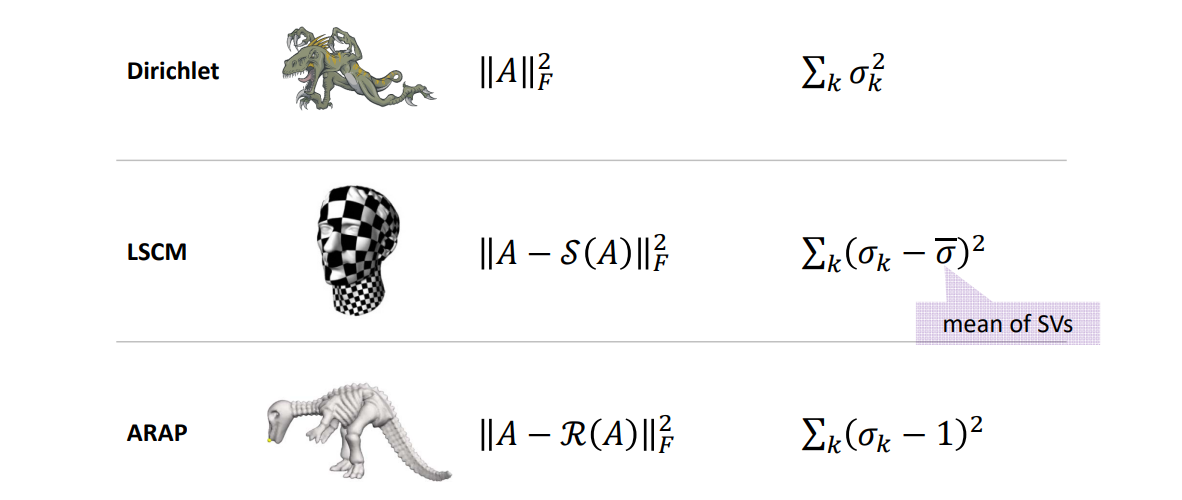
Summary

Geometric Mapping

• Discrete Mapping

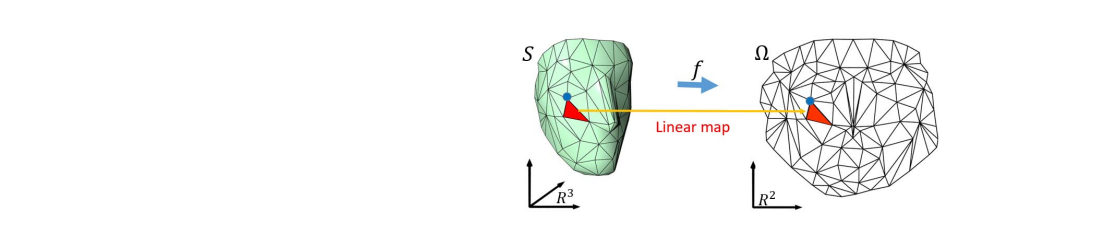
• Discrete formulation

argmin $E(\phi )$ Separable
s.t. $\phi \in K$

• Nonlinear and nonconvex
• Computationally expensive for large scale meshes!

Meshless mappings

$$f(x)=\sum_{i=1}^{m} c_iB_i(x)$$

[46:28] $f$有些独特的性质。例如在边界上满足一定的性质，就能保证内部一定满足某些性质。
对整个对象做映射，因此是meshless.

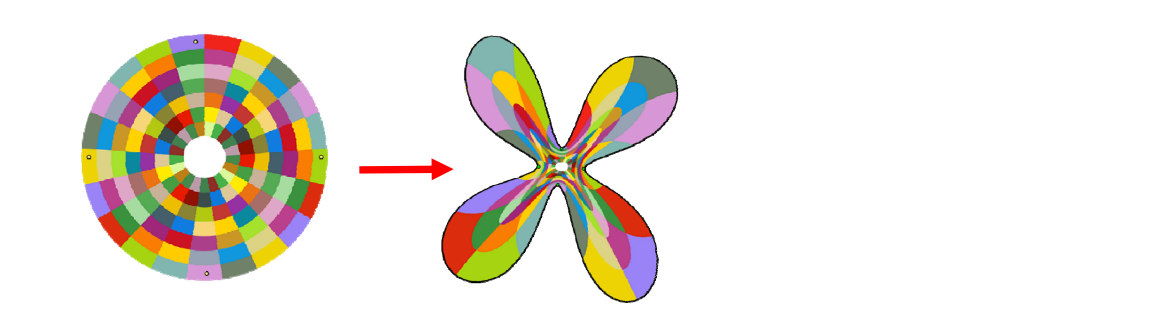
• Low distortion
• Flip‐free
• Bijective

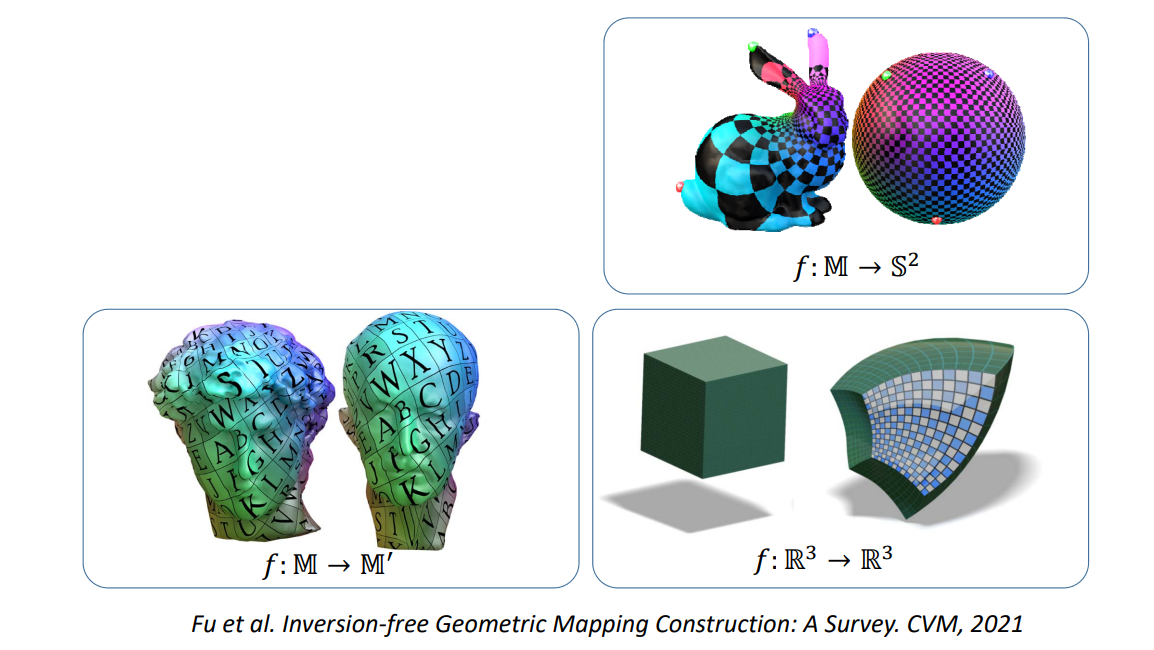
其他区域间的映射求解

• 离散形式
• 约束条件

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/