NURBS

定义

NURBS = Non‐Uniform Rational B‐Spline = 非均匀有理B样条

($𝑁^{(d)}_i$ :B‐spline basis function 𝑖 of degree d)

$$f(t)=\frac{\sum_{i=1}^{n}N_i^{(d)}(t)w_ip_i }{ \sum_{i=1}^{n}N_i^{(d)}(t)w_i}$$

• Uniform：均匀参数化，结点向量均匀
• Non‐Uniform：非均匀参数化，结点向量非均匀

非均匀,使用了非均匀的参数化，参数间距不一致，甚至有可能重合。

De Boor algorithm

similar to rational de Casteljau alg.

• option 1. – apply separately to numerator, denominator
• option 2. – normalize weights in each intermediate result

the second option is numerically more stable

这一部分没讲

影响NURBS曲线建模的因素

• 控制顶点：用户交互的手段
• 节点向量：决定了B样条基函数
• 权系数：也影响曲线的形状，生成圆锥曲线等

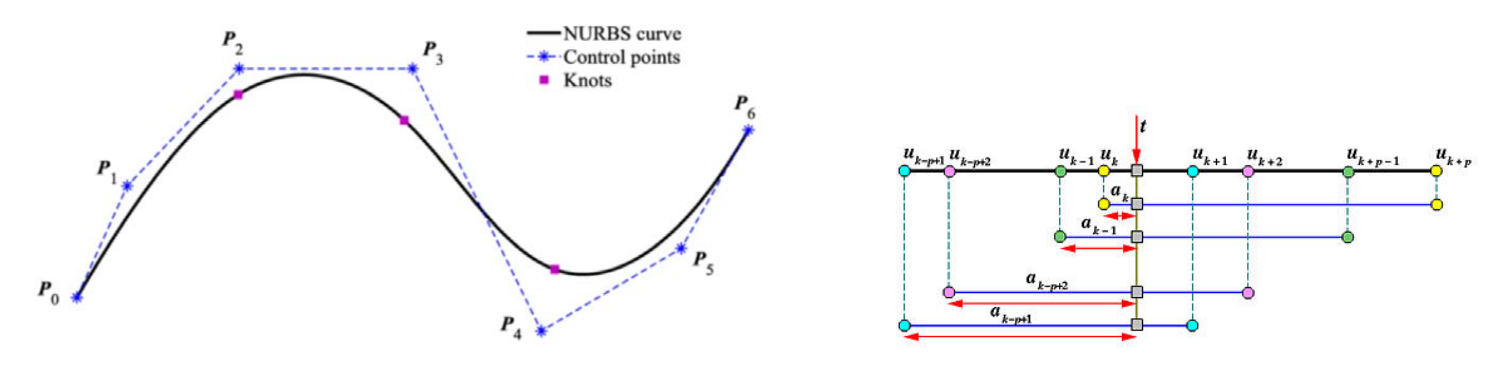
NURBS曲线的性质

大部分与Bezier/B样条曲线类同：具有良好的几何直观性

[24:18] 变差缩减：曲线与直线相交，其交点数不多于控制顶点的凸包与直线的交点数。
此性质用于曲线与直线求交。

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/