曲线的光顺方法

函数型3次样条曲线

小扰度假设：

• 转角不大于60°
• ${y}' (x)\ll 1$
• ${y}'' (x)\approx k(x)$

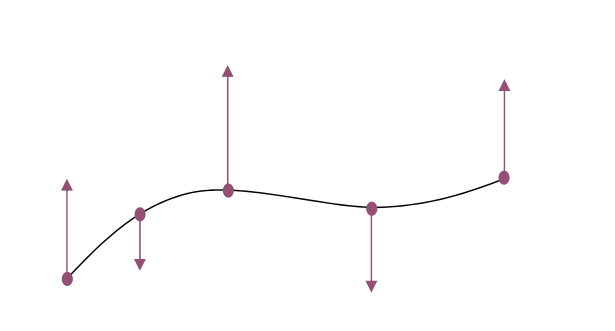
${y}' \ll 1⇒ 曲线的转角不会太大，此时 y"(x)=K(x)$
[?] $y"$不就是$K$吗？为什么需要这个前提条件？
工业界做高精设备时才需要考虑光顺。

光顺方法的基本思想

• $C^1$ continuous
• Decrease jump amplitude of curvature
• Decrease the first vibration number $R$
• Decrease the second vibration number $S$

具体步骤

这个框架适用于大部分问题：预处理 → 核心算法 → 后处理。
核心算法又可以分为粗处理 → 精处理

Step 1. 初光顺 Coarse fairing

• 定界法
  • Adjust the positions of control points
  • Decrease the jump amplitude of curvature
  • Remove some unwanted inflections
• Physical approach

Step 2. 基本光顺 Basic fairing

• 卡尺法
  • Adjust the positions of control points
  • Remove other redundant inflections
  • Decrease the first vibration number $R$
• Geometric approach

Step 3. 精光顺 Fine fairing

• 回弹法
  • Check the signs of shear force at control points
  • Adjust the change numbers of shear force
  • Decrease the second vibration number $S$
• Physical approach

B样条曲线的光顺方法

• 基于稀疏优化的光顺优化方法

$$\min_{\tilde{d} } ||e(\tilde{d} )||_1$$

$$s.t.||(\tilde{d} )-d||_\infty \le \varepsilon$$

曲率的二阶差分向量$e$. 计算公式如下：

$$e_i=\frac{C_{i+1}-C_i}{t_{i+1}-t_i} -\frac{C_{i}-C_{i-1}}{t_{i}-t_{i-1}},i=1,\cdots ,n-3$$

王士玮等，基于稀疏模型的曲线光顺算法，计算机辅助设计与图形学学报，2016.

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/