Bezier曲线

定义

\(n\)次Bezier曲线有\(n+1\)个控制顶点

$$ x(t)=\sum_{i=0}^{n} B^n_i(t)\cdot b_i $$

\(b_i\)称为控制顶点，所有\(b_i\)按顺序连起来得到的多边形为
控制多边形

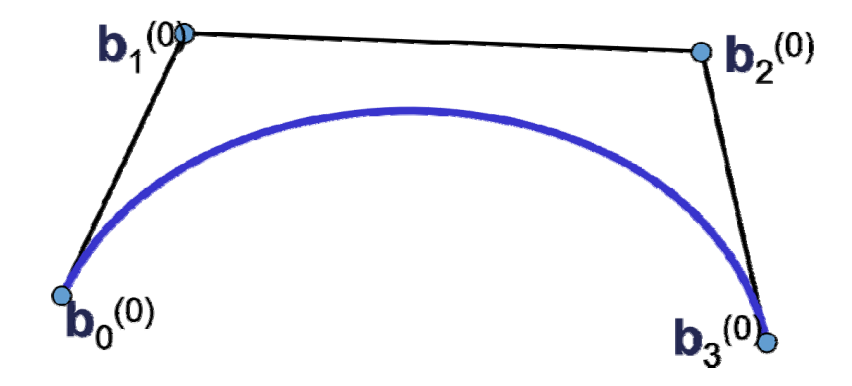
Bezier曲线的性质来源于Bernstein基函数的性质 （曲线是控制顶点的线性组合构成的，基函数提供了组合系数）

属性

• 起始点同p0位置
• 起点处的切线方向同\(\vec{p_0p_1}\)
• 终点同为p3位置
• 终点处的切线方向同\(\vec{p_2p_3}\)

例子

3次Bezier曲线

$$ f(t)=\sum_{i=1}^{3} B^3_ip_i, \quad t\in [0,1] $$

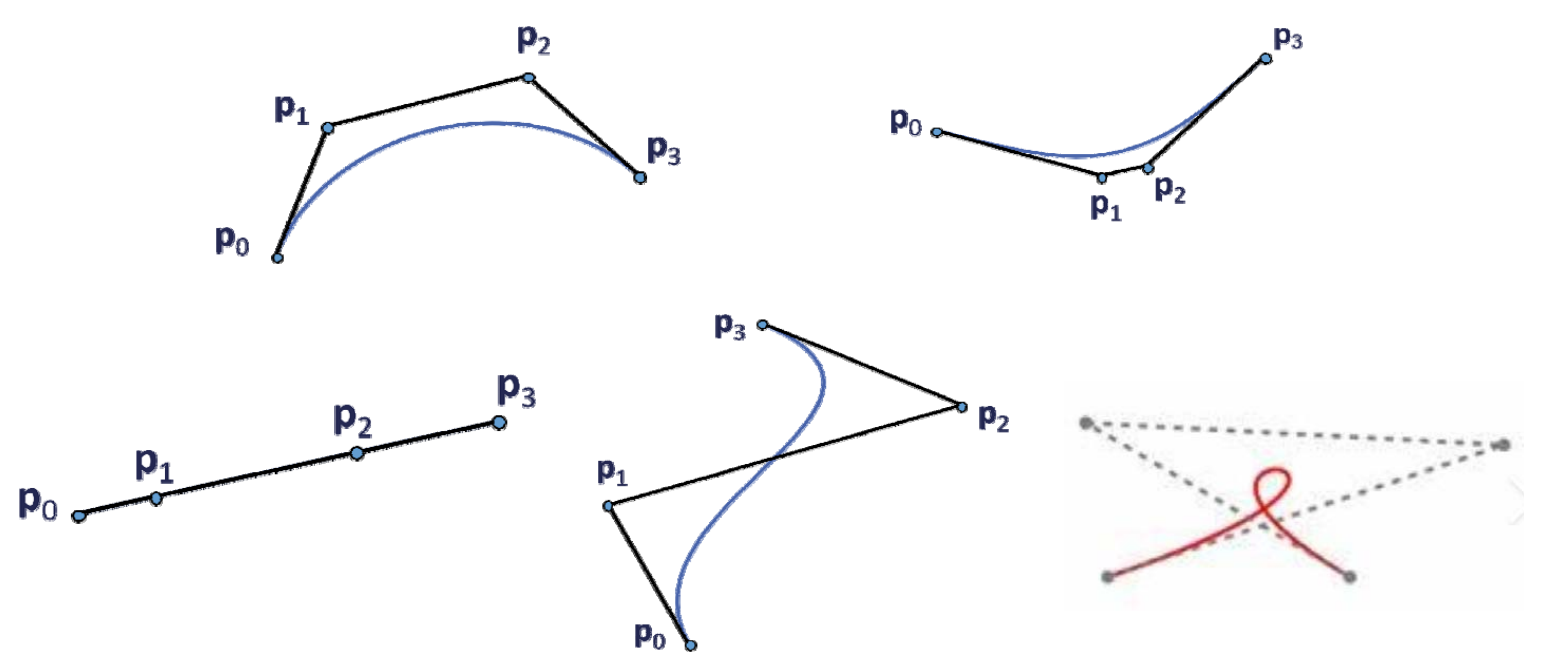
更复杂的Bezier曲线

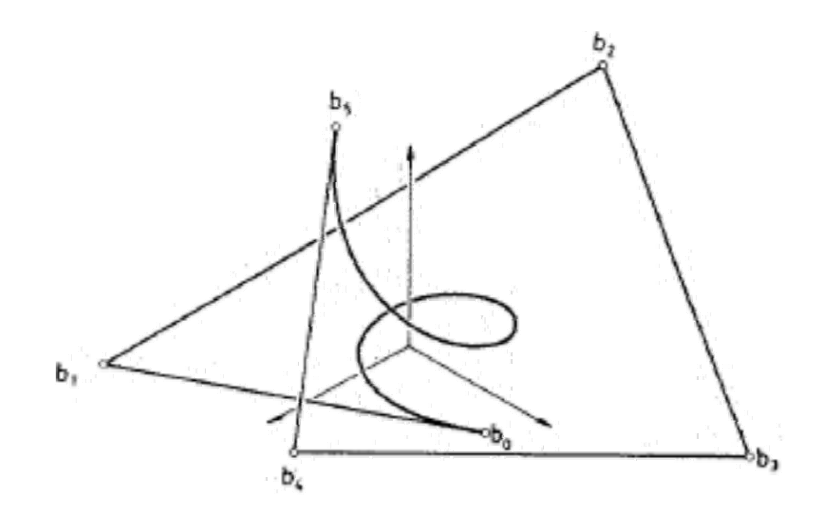
3D空间的Bezier曲线（单参数）

$$ f(t)=\sum_{i=1}^{n} B^n_ip_i,t\in [0,1] $$

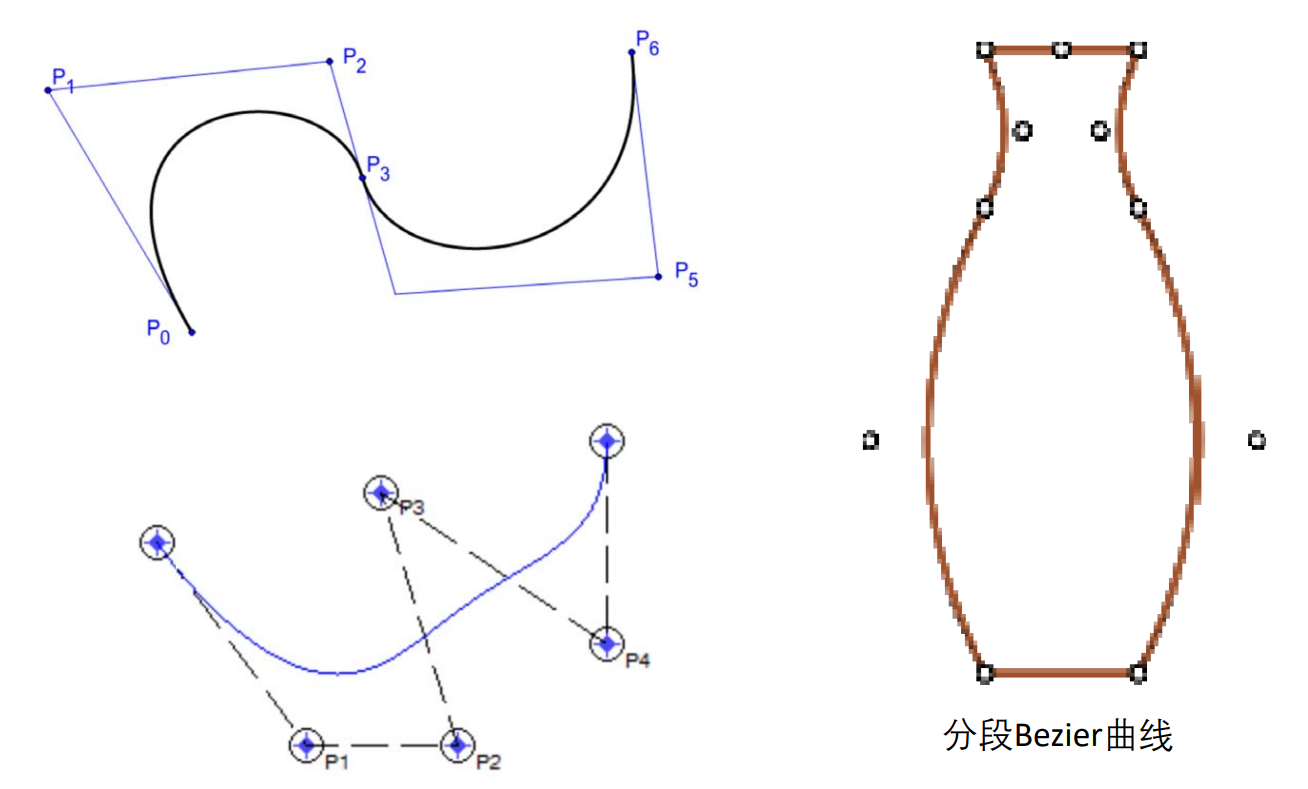
Piece-wise Bezier曲线

[38:23] 当控制点比较多时，Bezier曲线不利于控制

• How

把多个点分段，每4个点画一条曲线，例如photoshop中的钢笔功能。

• What

光滑的Piece-wise Bezier曲线

C0连续：数值上连续

C1连续：切线连续（方向和大小都要一致），即光滑

C2连续：曲率连续

要使分段的Bezier曲线光滑（C1连续），需要让上一段的终点和下一段的起点切线一致。这可以通过控制点的位置来实现。

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/