Trimmed NURBS曲面
Trimmed:裁剪
Trimmed NURBS曲面:表达带“洞”的曲面
(1)在曲面上定义曲线:使用参数域上的NURBS曲线来定义,然后复合得到曲面上的曲线
(2)用曲线来表达曲面上的洞
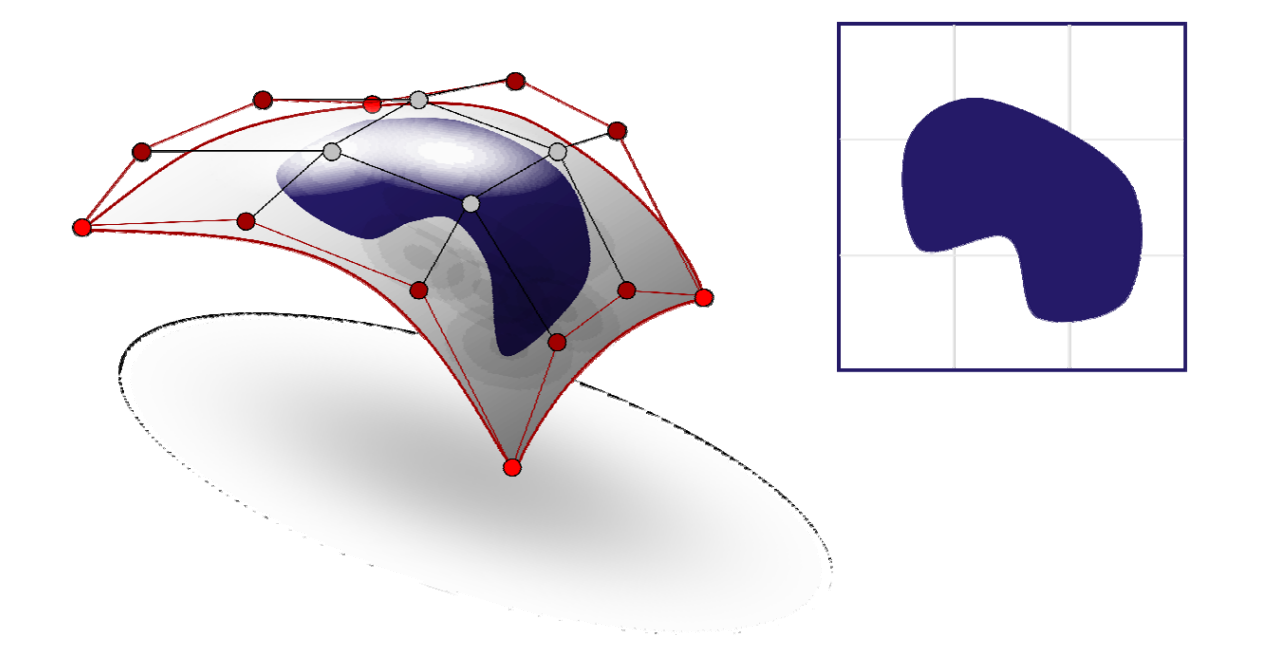
三角域上的Bezier曲面片
背景:张量积形式的 Bezier 曲面定义在矩形曲域,表达很不灵活,难以应用于非规整曲面。
定义在三角面片上的类似于 Bezier 的曲面。
三角域的Bernstein‐Bezier曲面片:表达非矩形边界的曲面
• 矩形域有时不方便
• 使用三角域来定义曲面片
三角Bezier曲面片
$$ F(x)=\sum_{i+j+k=n;i,j,k\ge0}^{} \frac{n!}{i!j!k!} \alpha ^i\beta ^j\gamma ^kp_{i,j,k} $$
$$ x=\alpha a+\beta b+\gamma c,\alpha +\beta +\gamma =1 $$
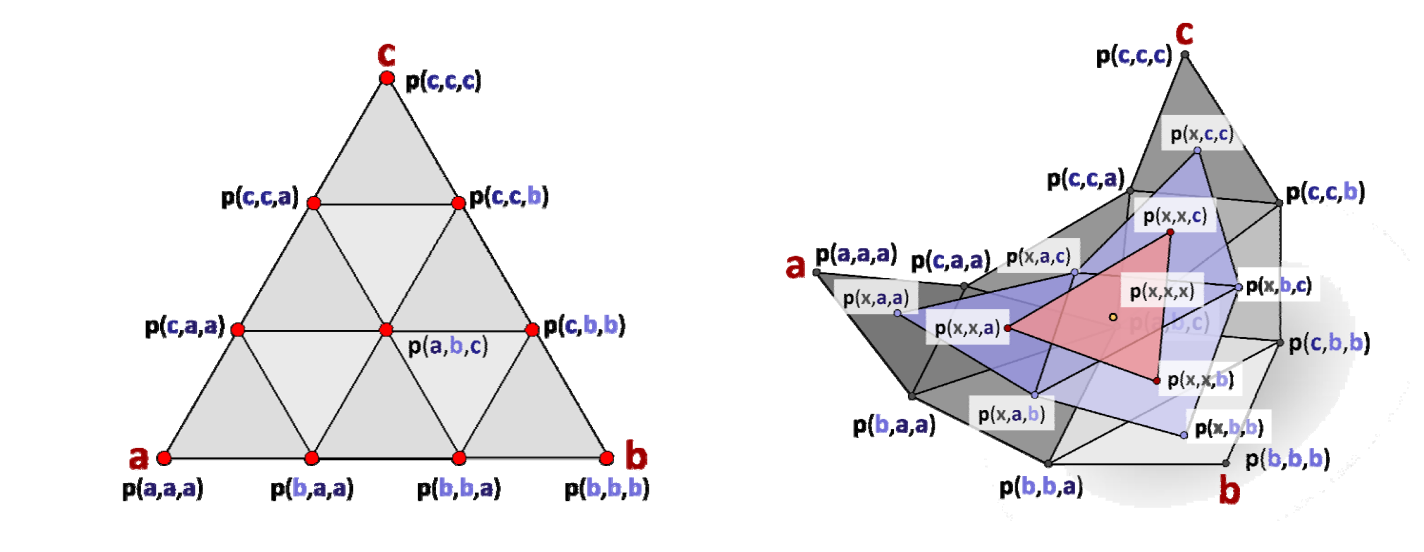
\(\alpha ,\beta ,\gamma \) 为三角形上某个点的重心坐标。
连续性
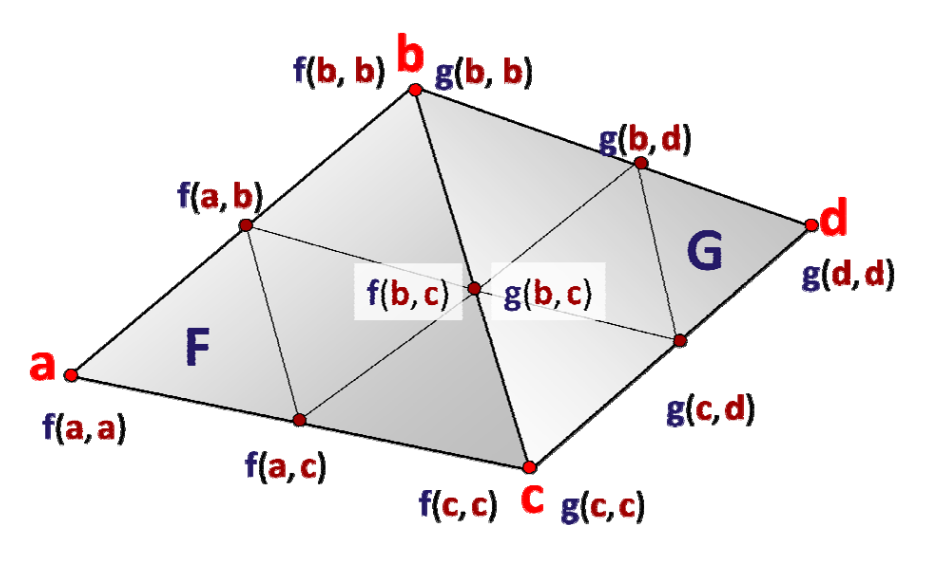
张量积体(三参数)
Bezier体
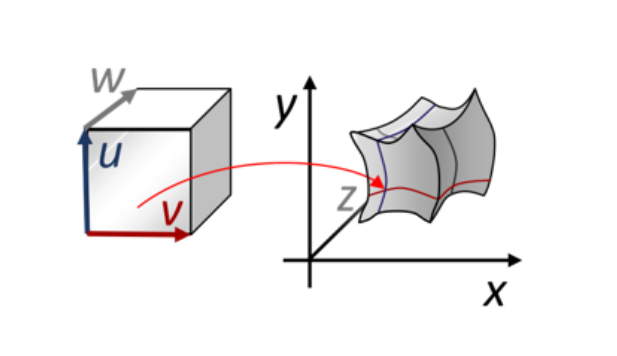
张量积曲面总结
• 两个独立方向的“曲线的曲线”
• 性质大都类同于曲线的性质
• 表达、公式形式比曲线情形复杂
• 特殊问题:角点的光滑性
本文出自CaterpillarStudyGroup,转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/