Mesh Parameterization (Mesh Flattening)
什么是曲面参数化
对于一个二维流形的三维曲面,把它拍成二维的过程称为参数化。
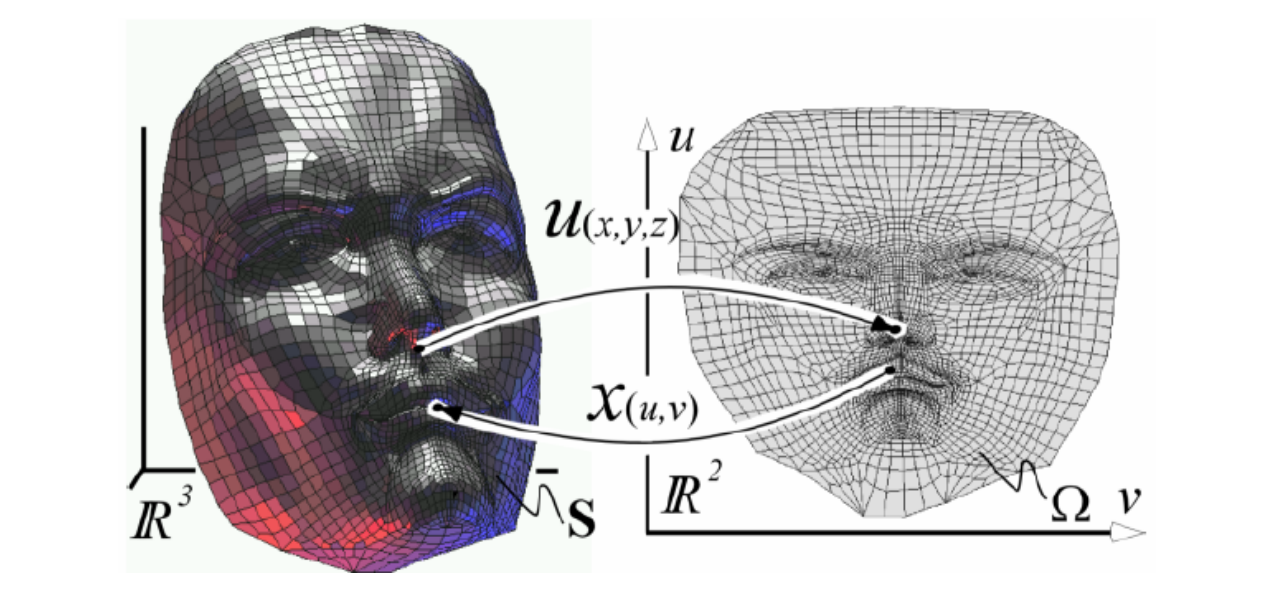
- 每个3D顶点(\(x,y,z\))对应一个2D点(\(u,v\))
• (\(u,v\)) 称为 (\(x,y,z\)) 的参数(2D流形曲面的本征维数)
曲面参数化要解决的问题
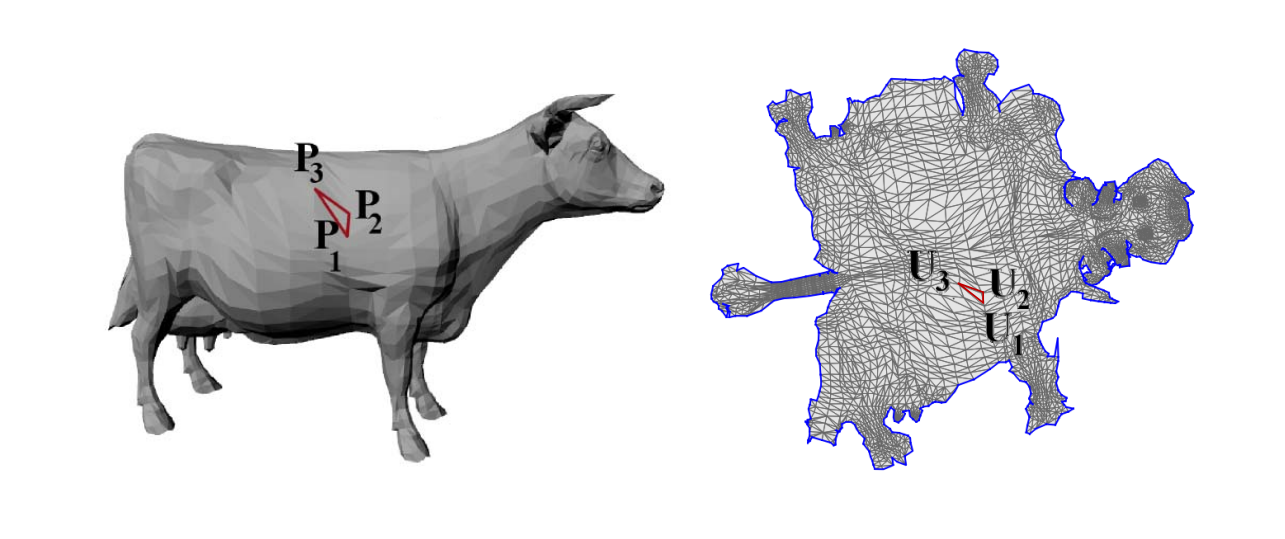
非可展曲面展开后必须形变,因此希望展开后的平面形变尽量地少,具体衡量为:
- 三角形不能发生翻转。
- 三角形的扭曲能够保持。
- 边界不要自交。
这节课为曲面参数化的基础课,不涉及这些内容,将在后面展开。
参数化的应用
- 提供了三维曲面每个点的一个二维参数,可用于贴纹理
- 在低维来处理高维问题,减少复杂度
- 三维曲面之间的相关问题可通过参数化空间来处理
曲面参数化的方法:Tutte’s Method
第一步:将边界映射到平面的凸多边形上
[Floater 97’]
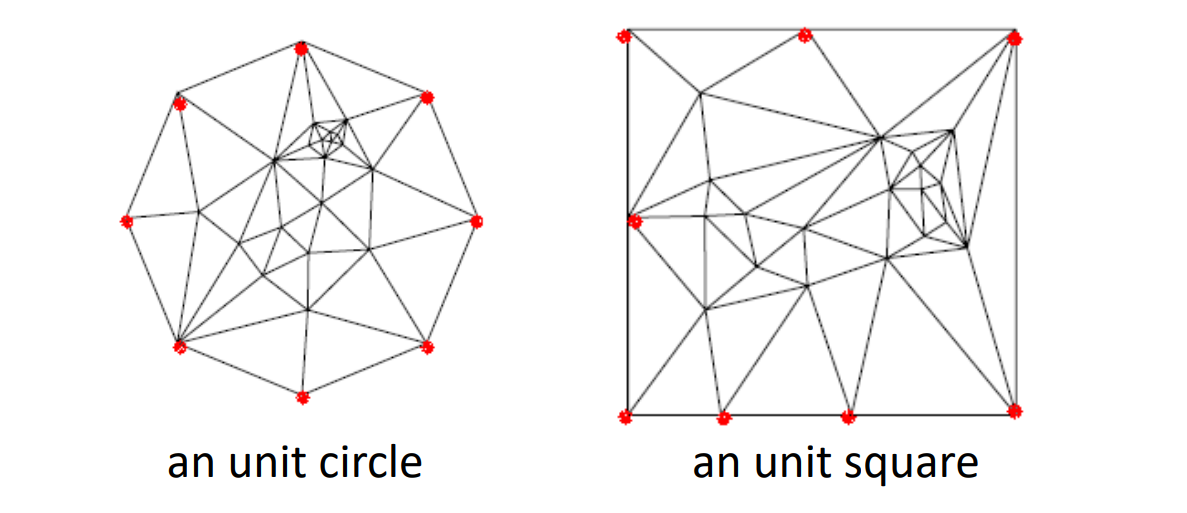
M. Floater. Parametrization and smooth approximation of surface triangulations. CAGD, 1997.
http://www.cs.jhu.edu/~misha/Fall09/Floater97.pdf
第二步:求解稀疏方程组
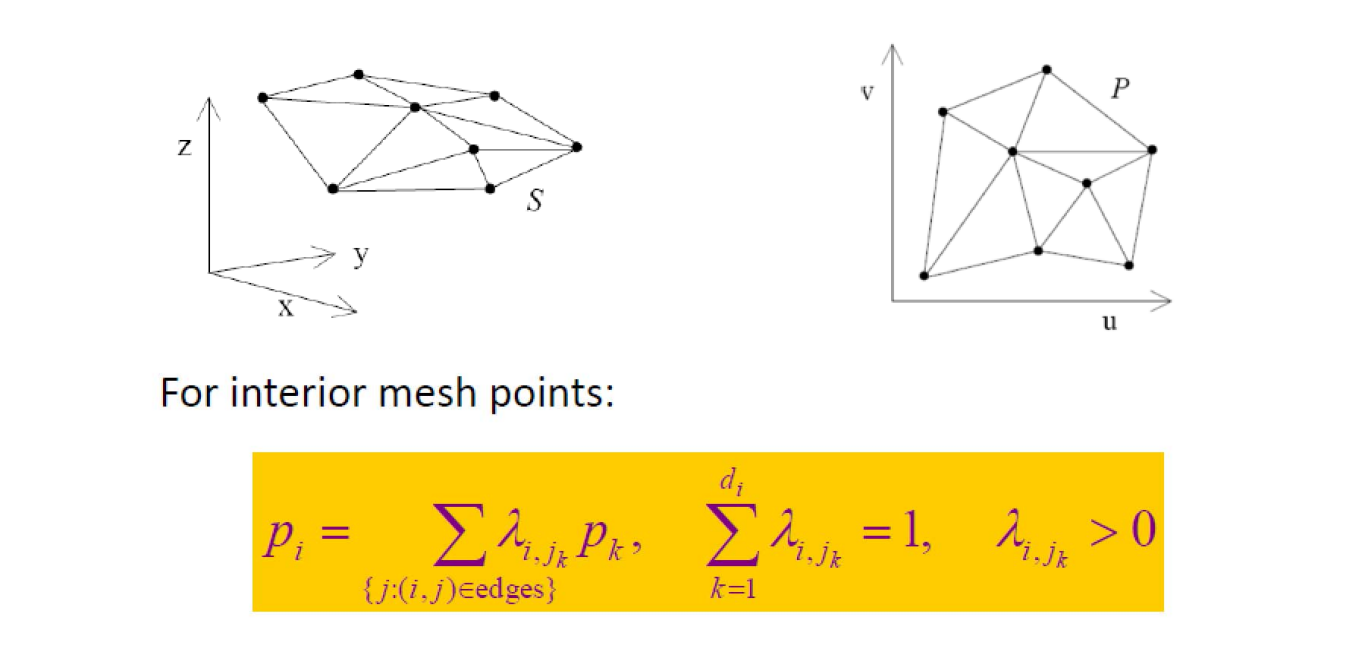
Forming a sparse linear system
还是之前 Global Laplacian Smoothing 求极小曲面的原理。
边界点在同一平面上,得到的极小曲面也是在平面上的。
但是要把边界点放右边呢?因为右边是固定点,要求的是内部点。
性质
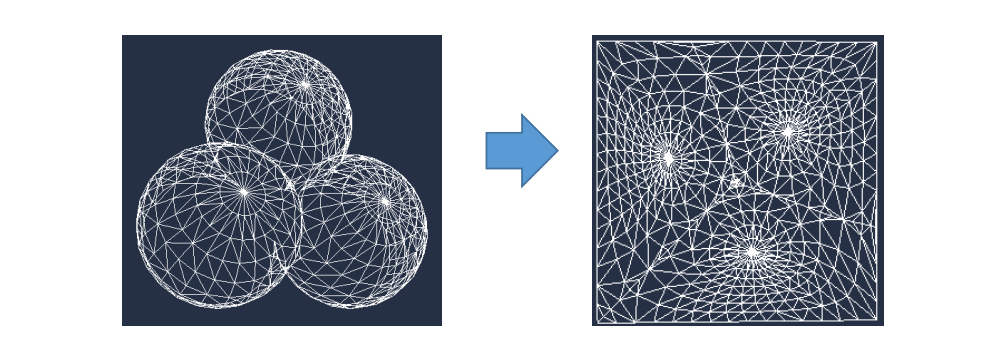
- 优点:
简单
如果边界位于凸多边形上,则三角形一定不会发生翻转! - 缺点:
扭曲大
在密的地方容易发生数值上的精度问题 - 其它 第二步中使用不同的权值定义方向得到的结果不同,使用cot权的扭曲最小
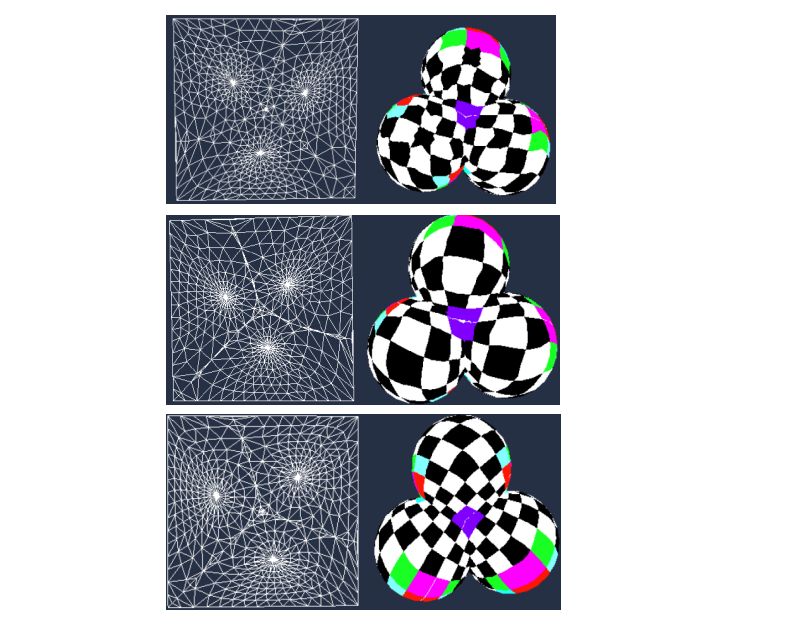
使用这种格子作为纹理,方便观察扭曲情况,仍建议用 cotangent 权,扭曲较小。
图1:均匀权, 图3:cotangent权
操作步骤总结
• 检测边界
• 将边界映射到正方形边界或圆边界(凸边界)
• 构建稀疏方程组
• 求解稀疏方程组
• 更新顶点坐标
• 连接纹理图像,更新显示
分块参数化
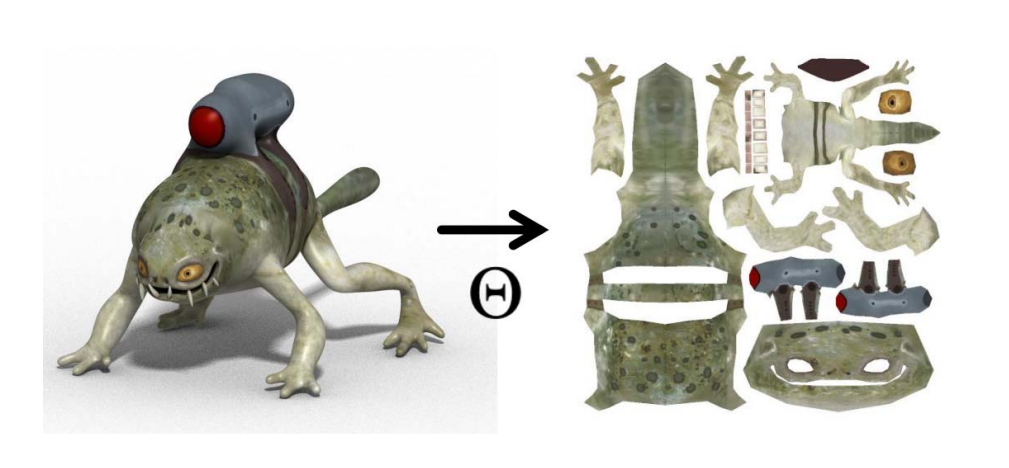
复杂模型割成多块分别参数化,再 packing
优点:1.减少扭曲。 2.具有语义。
缺点:1.空间浪费。
本文出自CaterpillarStudyGroup,转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/