参数曲面

link

张量积曲面

定义

张量积：link

$$f(u,v)=\sum_{i=1}^{n} \sum_{j=1}^{n}b_i(u)b_j(v)p_{i,j}$$

$$=\sum_{i=1}^{n} b_i(u)\sum_{j=1}^{n}b_j(v)p_{i,j}$$

$$=\sum_{j=1}^{n} b_j(v)\sum_{i=1}^{n}b_{i}(u)p_{i,j}$$

曲面是曲线的曲线
先沿一个方向做，然后再沿另一个方向做（方向顺序无关）

张量积曲面的性质

类似于曲线情形，性质取决于基函数的性质

Bezier曲面

定义

基于张量基定义的形式，以Bizier基定义的曲面

$$f(u,v)=\sum_{i=1}^{d} \sum_{j=0}^{d}B_i^{(d)}(u)B_j^{(d)}(v)p_{i,j}$$

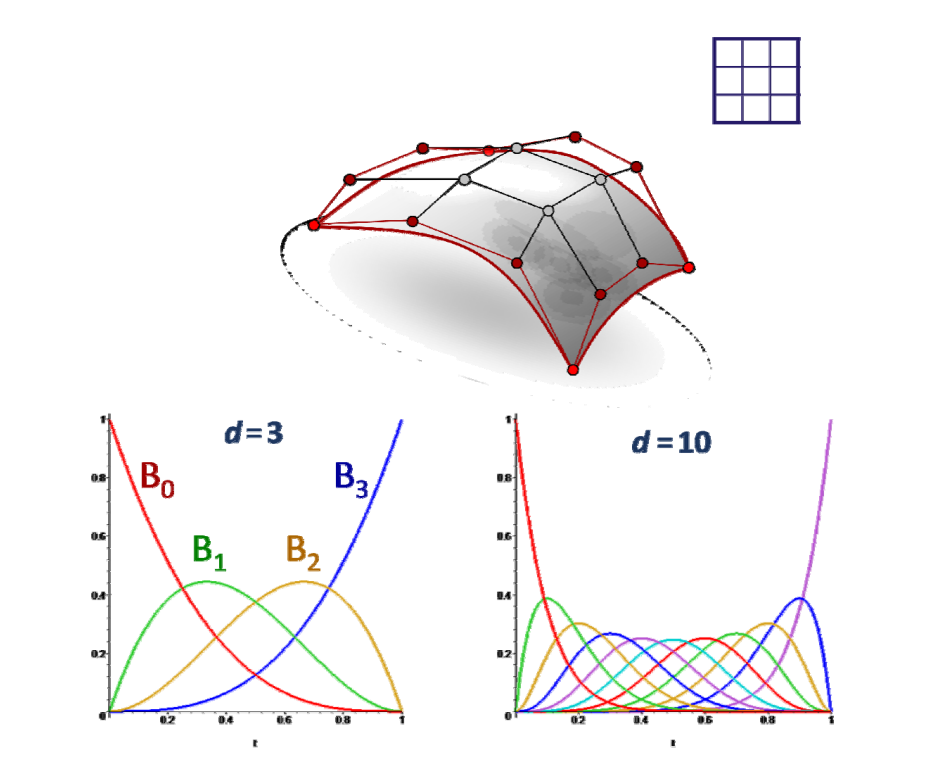
Bezier曲面的性质

• 边界插值

• 凸包

• 变差缩减

• 几何作图法
  

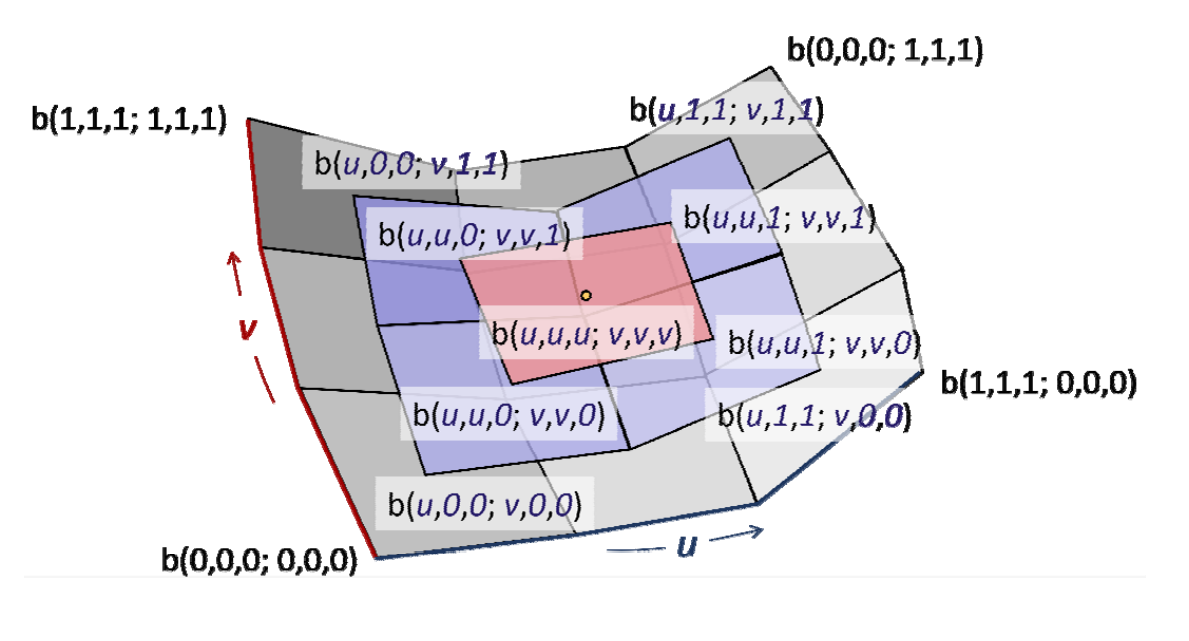
• 曲面片之间的拼接连续性

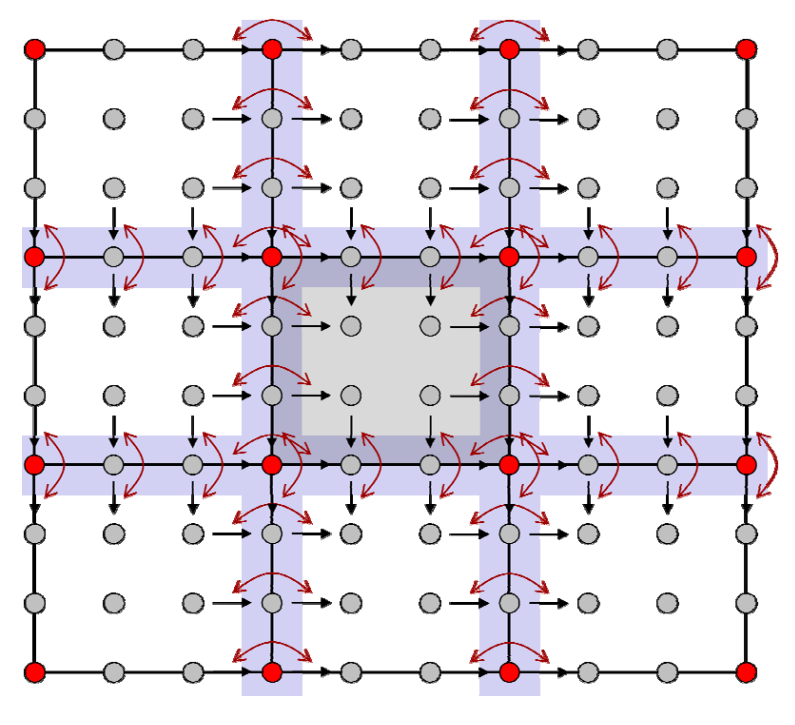
其他曲面

• B样条曲面

• 有理曲面

• NURBS曲面

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/