[1:11:23] # Modeling
公式中的 a,b,c都是2D的向量。
[1:12:38] # Modeling
把三个系数 a,b,c 看作是曲线的控制顶点,发现顶点的位置与曲线没有关系,不直观,不利于设计。
把幂基换成 Berstein 基,控制点与曲线的关系变得直观。
回顾:曲面重建
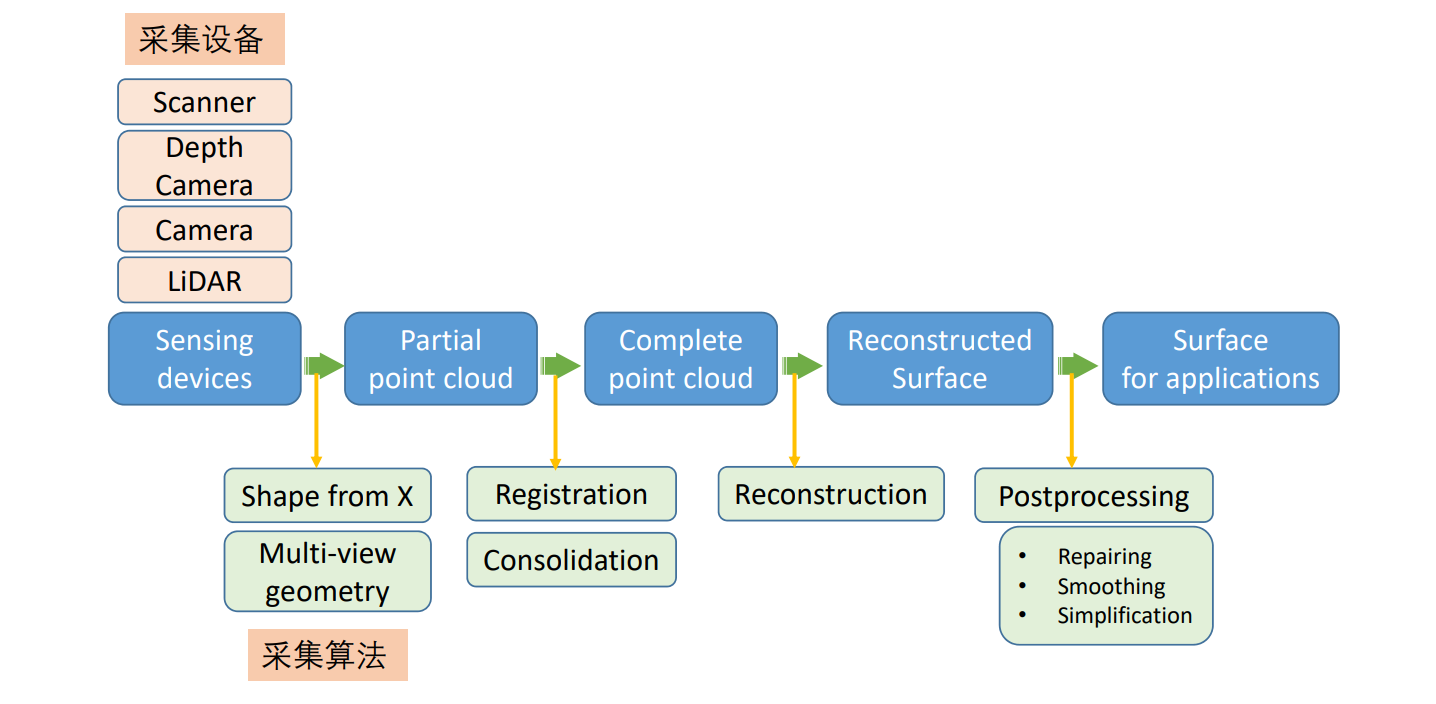
建模(modeling):设计与重建
- 曲面设计(Design)
- 不存在的物体:通过人工交互凭空设计出新的物体
- CAGD (NURBS)、mesh modeling
- 存在的物体:通过人工交互编辑修改构建出新的物体
- Editing, deformation
- 不存在的物体:通过人工交互凭空设计出新的物体
- 曲面重建(Reconstruction)
- 存在的物体:对其采集并进行数字化构建
- 也称为:逆向工程、扫描重建
- Reverse engineering, scanning
Surface Editing
Design Modeling
-
Design from zero
• Create a shape by a set of 3D design operators such as extrusion or revolution etc. -
Design from a given shape (Mesh editing)
• Select a base shape
• Select editing elements and editing operators
• Deform the shape to obtain a new shape
Mesh Surface Editing
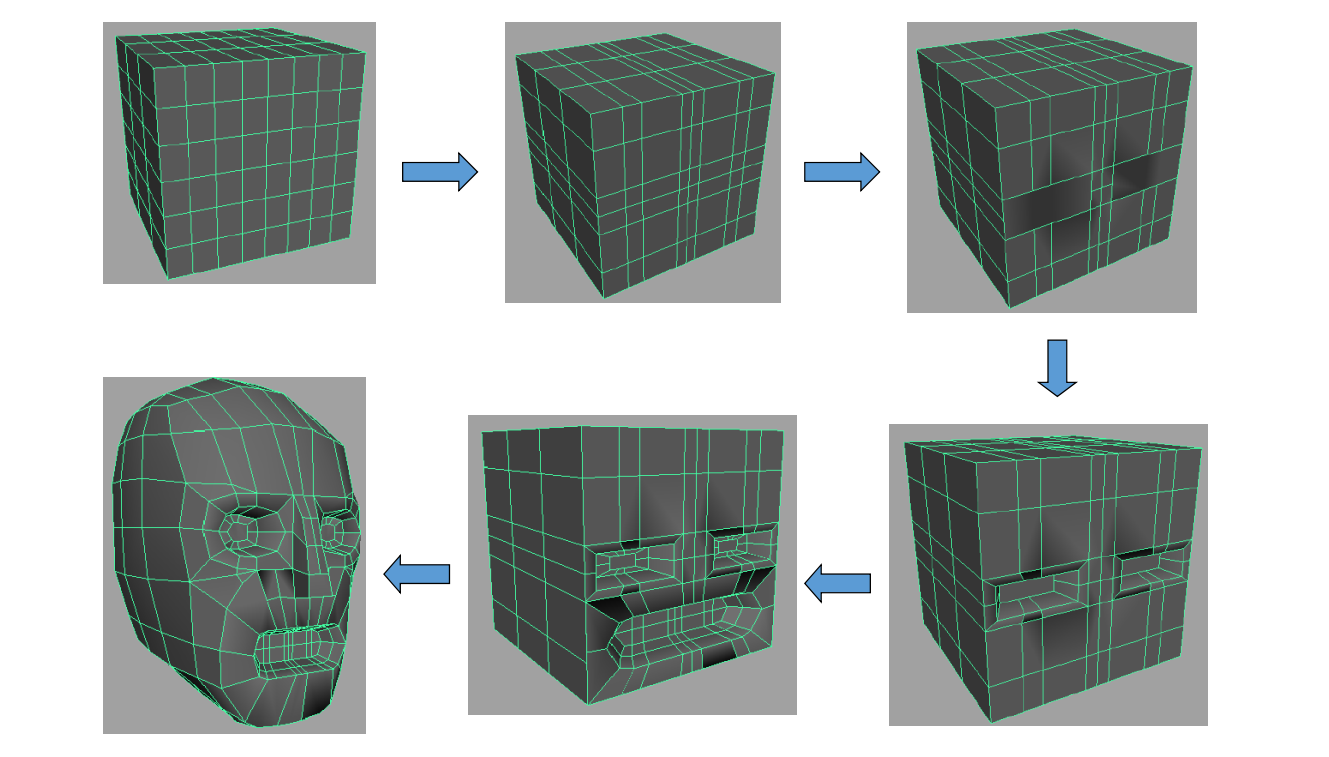
Interactive shape modeling
- Modeling is an interactive, iterative process
• Tools need to be intuitive (interface and outcome)
• Allow quick experimentation
• Preserve shape properties
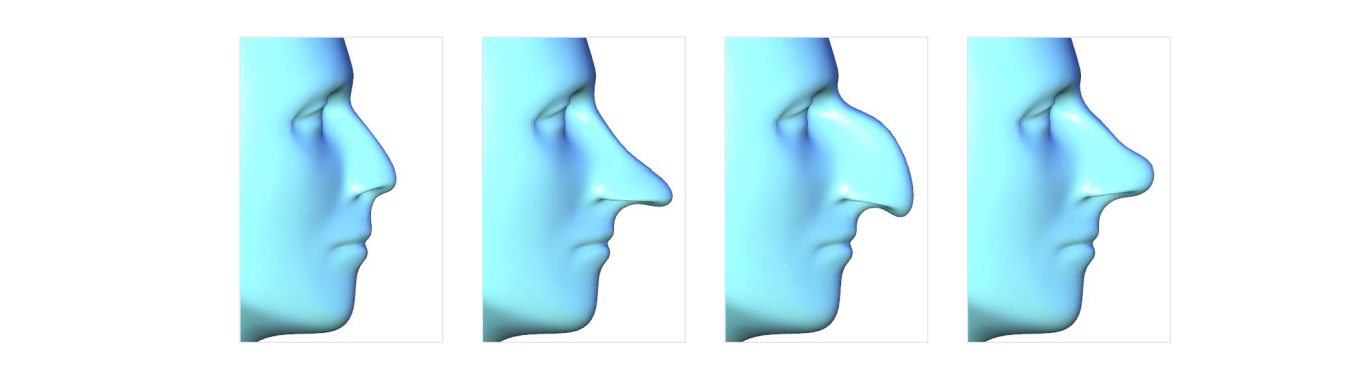
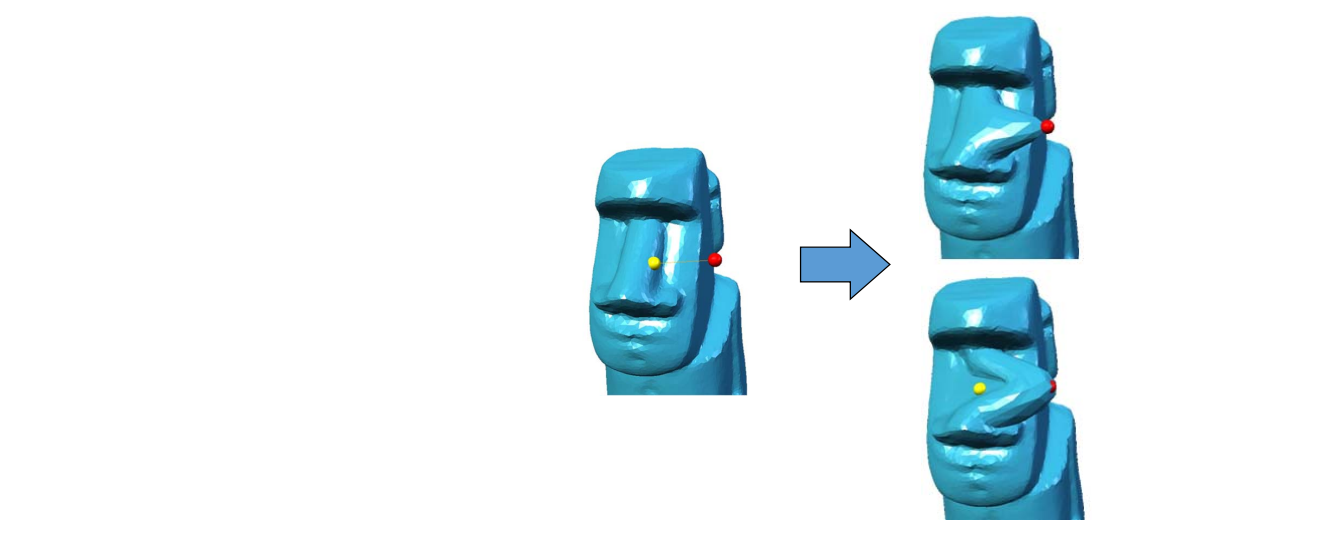
User Interaction (UI)
- User specifications: Intuitive, easy‐to‐use
• Dragging handles ‐‐ vertices, features, ROI, … - Deformed shape: adapt to user intents
Challenges:
• Operations
• Preservation of properties
• Semantics
Methodology
- Set a proxy P for the input shape S
- P is simpler/easier/more semantic than S
- Find a map between P and S: S=g(P)
- g is also called an embedded space
- User interacts and deforms the proxy P to P’
- Find a deformation map: P’=h(P)
- Compute a new shape S’ from P’: S’=g(P’)
Key Problem:
• find a good map g
- 第一步:Set a proxy P for the input shape S
P is simpler/easier/more semantic than S - 第二步: Find a map between P and S: S=g(P)
g is also called an embedded space
find a good map g 是关键
- 第三步:User interacts and deforms the proxy P to P’
Find a deformation map: P’=g(P) - 第四步:Compute a new shape S’ from P’: S’=g(P’)
Proxy Shapes (handles)
- Points
• Points, vertices, … - Lines/Curves
• Sketches, skeletons, silhouettes, wires, … - Meshes
• Bezier nets, lattices, cages, … - Other shapes
• Deformation transfer: learning deformation from other shapes
本文出自CaterpillarStudyGroup,转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/