Bezier曲线存在的问题

Bézier曲线无法表示圆弧！

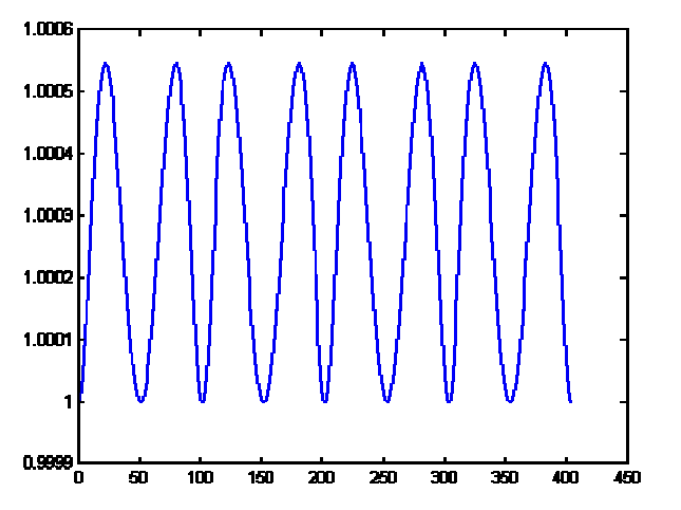
Evaluation of \((𝒙^𝟐+𝒚^𝟐)\) for points on the Bezier curve

投影几何

齐次坐标：\(x\longrightarrow \binom{wx}{w} \)

例如：

• 2D case:

$$ \binom{x}{y} →\begin{pmatrix}wx  \\wy  \\w \end{pmatrix} $$

• 3D case:

$$ \begin{pmatrix}x  \\y  \\z \end{pmatrix} →\begin{pmatrix}wx  \\wy  \\wz  \\w \end{pmatrix} $$

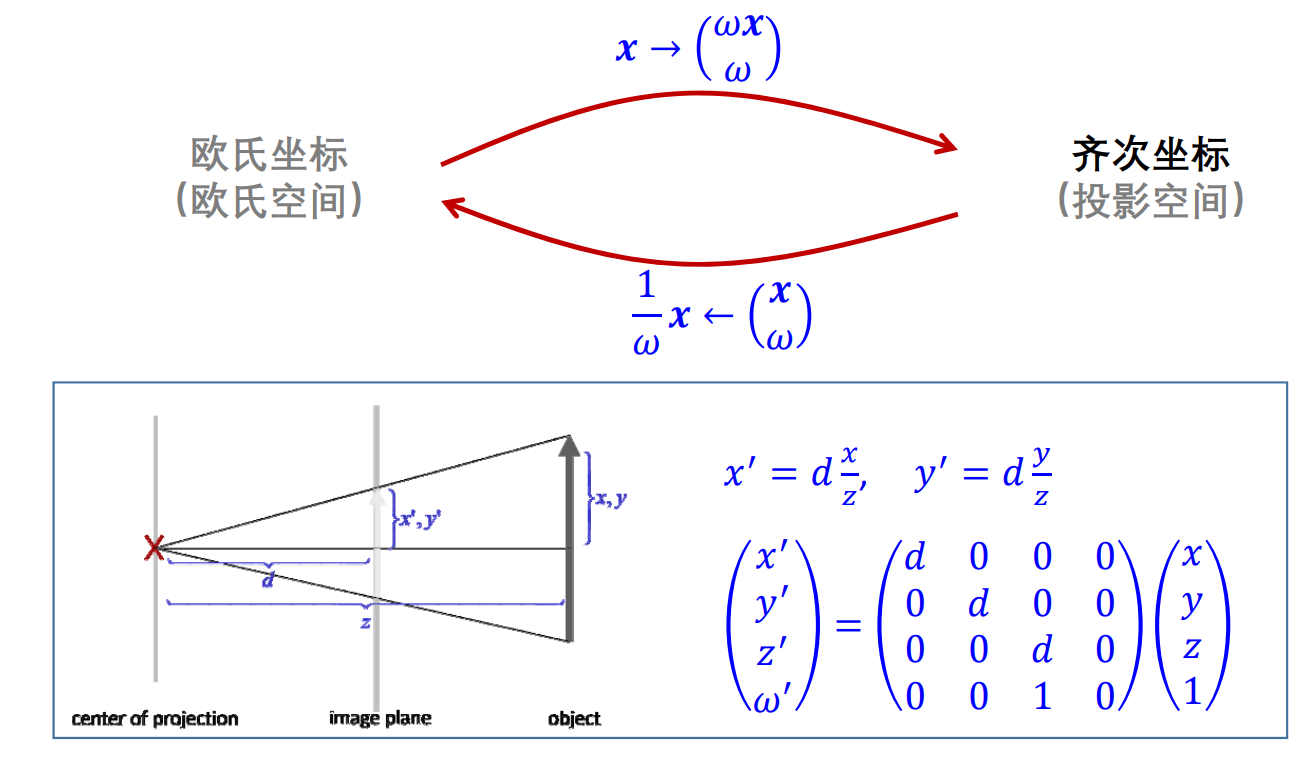
用欧式坐标表达的空间称为欧氏空间。用齐次坐标表达的空间称为投影空间

构造有理Bezier曲线

基本形式

构造\(\mathbb{R} ^n\)空间中的d阶有理Bezier曲线
（1）在\(n+1\)维空间定义 d阶Bezier 曲线

$$ 𝒇^{(hom)}(t)=\sum_{i=0}^{n}B_i^{(d)}(t)P_i,P_i\in \mathbb{R} ^{n+1} $$

（2）把最后一个维度作为齐次项
（3）再通过除法映射到\(n\)维,得到欧氏空间的曲线n

$$ 𝒇^{(eucl)}(t)=\frac{\sum_{i=0}^{n}B_i^{(d)}(t)\begin{pmatrix}p_i^{(1)}  \\\cdots  \\p_i^{(n)} \end{pmatrix}}{\sum_{i=0}^{n}B_i^{(d)}(t)P_i^{(n+1)}} $$

一般形式

每个控制顶点上设置一个权系数

$$ {f}^{(eucl)} (t)=\frac{\sum_{i=0}^{n}B_i^{(d)} (t)w_ip_i}{\sum_{i=0}^{n}B_i^{(d)} (t)w_i } $$

$$ p_i=\begin{pmatrix}p_i^{(1)}  \\\cdots  \\p_i^{(n)} \end{pmatrix} $$

另一种形式

$$ {f}^{(eucl)} (t)=\sum_{i=0}^{n}p_i =\frac{B_i^{(d)} (t)w_i}{\sum_{i=0}^{n}B_i^{(d)} (t)w_i } =\sum_{i=0}^{n}q_i(t)p_i $$

with \(\sum_{i=0}^{n} q_i(t)=1\)

如权系数都相等，则退化为Bezier曲线

也可以看作是权函数\(q_i(t)\)变成了有理形式的权函数。

有理Bezier曲线的几何解释

几何解释

高维的Bezier曲线的中心投影

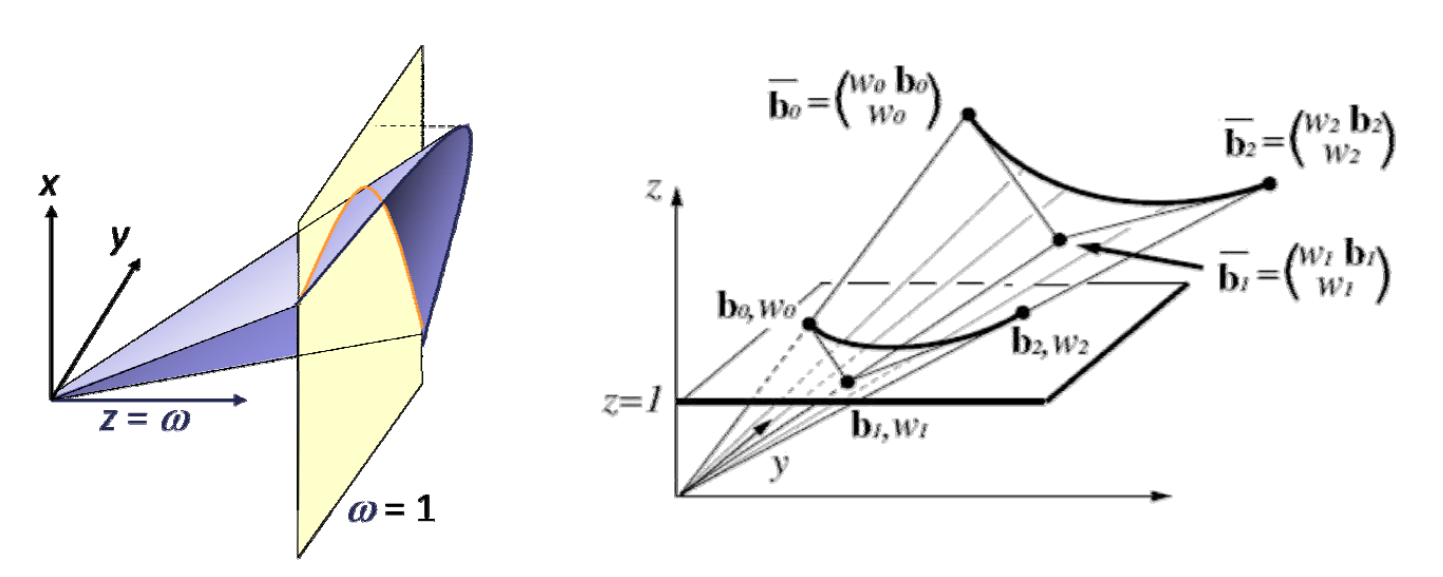
3D空间中的多项式曲线投影到2D有可能是圆。因为3D坐标到2D坐标的转换要经过一个除法。
数学上的有理是带分母的意思。

2次有理Bezier曲线表示圆

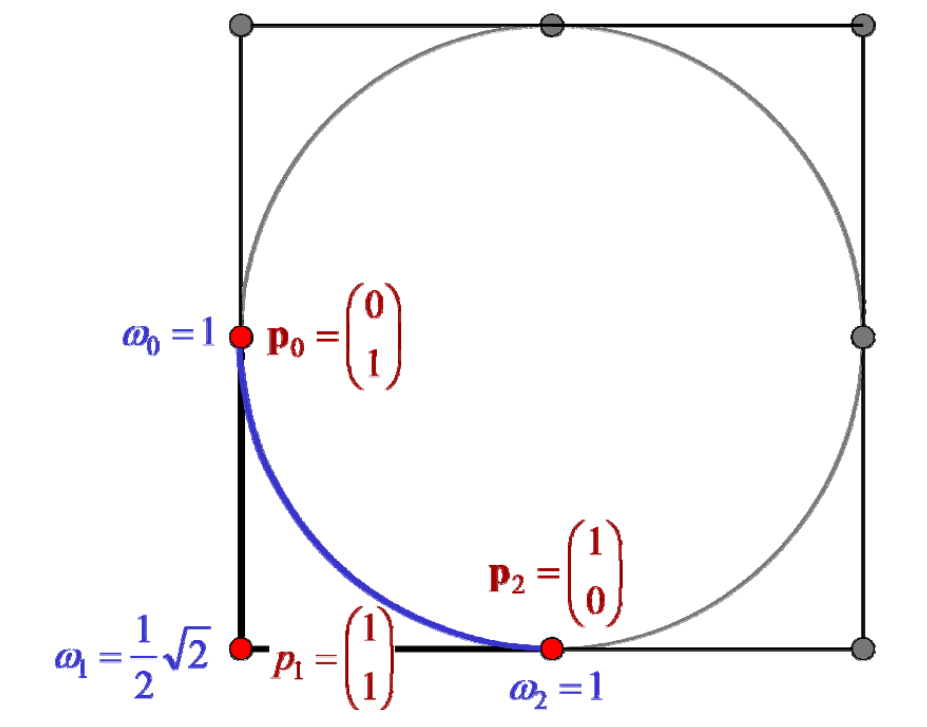
权系数对曲线形状的影响

控制顶点的权系数越大，曲线就越靠近该点

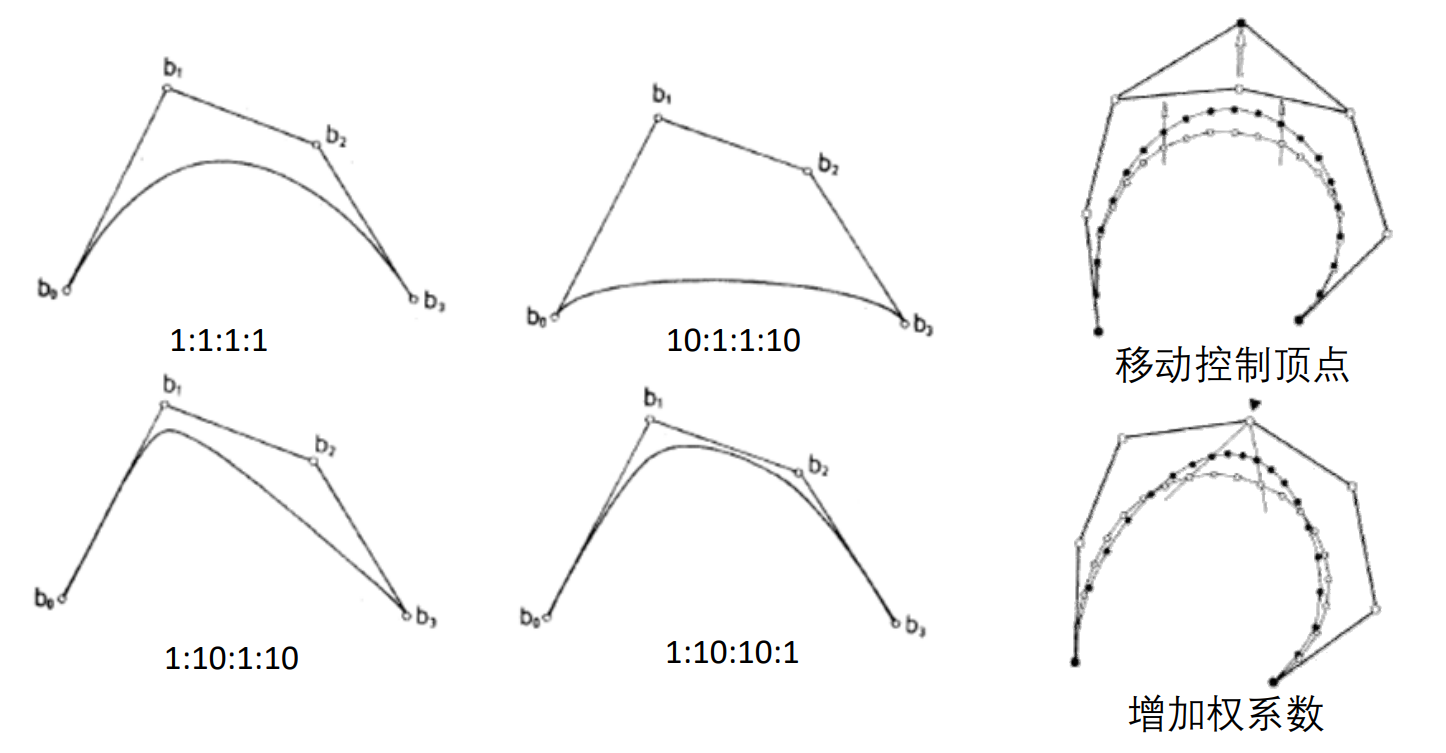
调整控制顶点的位置或权重都能控制曲线。

有理Bezier曲线的性质

具有Bezier曲线的大部分性质(设\(w_i>0,i=1\sim n\)):
• 端点插值
• 端点切线
• 凸包性
• 导数递推性
• de Casteljau作图算法
• …

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/