极小曲面

• 平均曲率处处为0的曲面

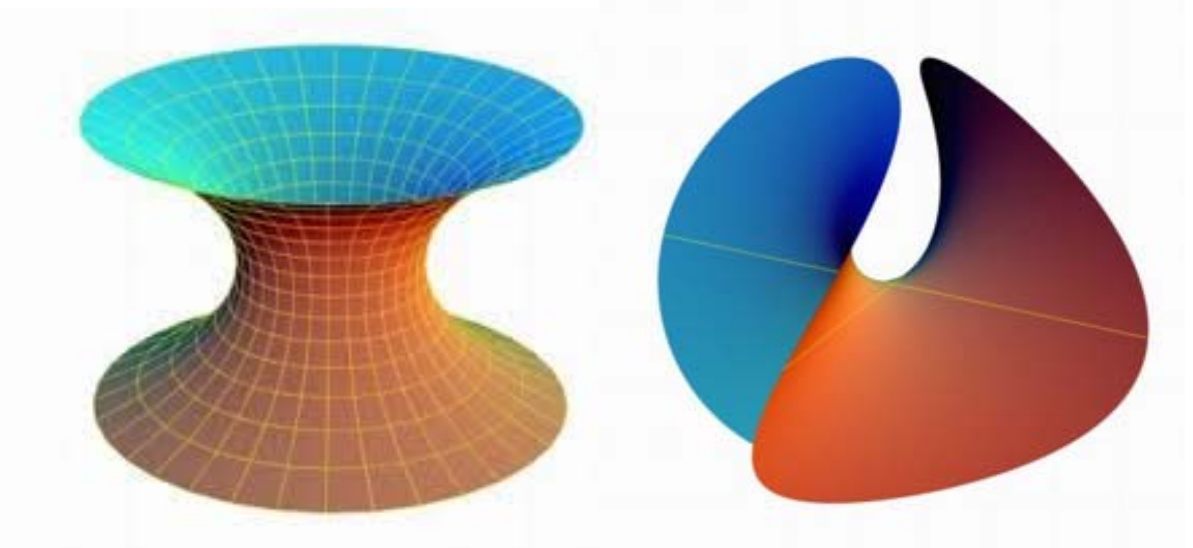
每个点都是马鞍点
常见的极小曲面肥皂泡。

建筑中使用极小曲面，好看、省材料、不积水

极小曲面的平均曲率流

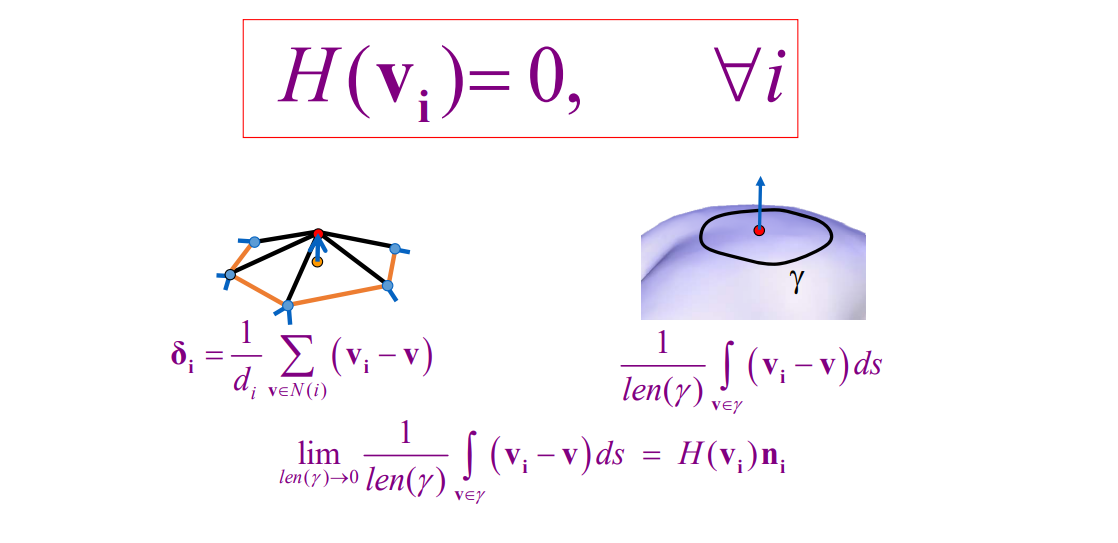
Laplace Operator (Umbrella Operator)

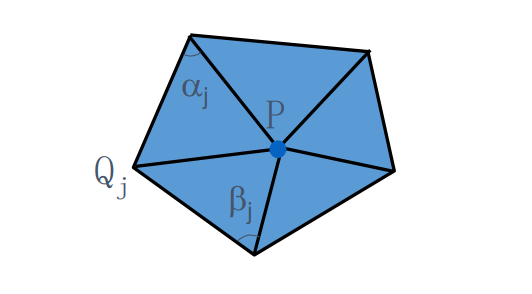
Mean 曲率处处为0，代入 Mean Curve 的计算公式

$$ K=\frac{1}{2A_m} \sum (\cot \alpha_{ij}+\cot \beta_{ij})(x_i-x_j)=0 $$

以上公式可以看作是 V 与其 1 邻域点的线性组合，得到 Q 平面内的重心坐标点。

任意一个曲面，把P往Q方向移动，就可以得到极小曲面：

$$ L(P)=\frac{1}{n} \sum_{i=1}^{n} \overrightarrow{PQ_i} =\frac{1}{n} \sum_{i=1}^{n}Q_i-P $$

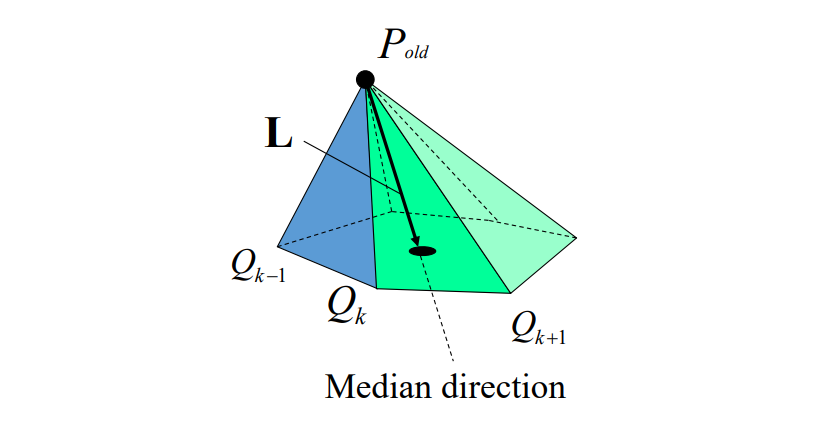
但是不建议直接把P移动Q点，而是每次移一小部分。

• 因为每个点的运动是互相影响的，一个点变化太大，它邻居的目标就不对了。

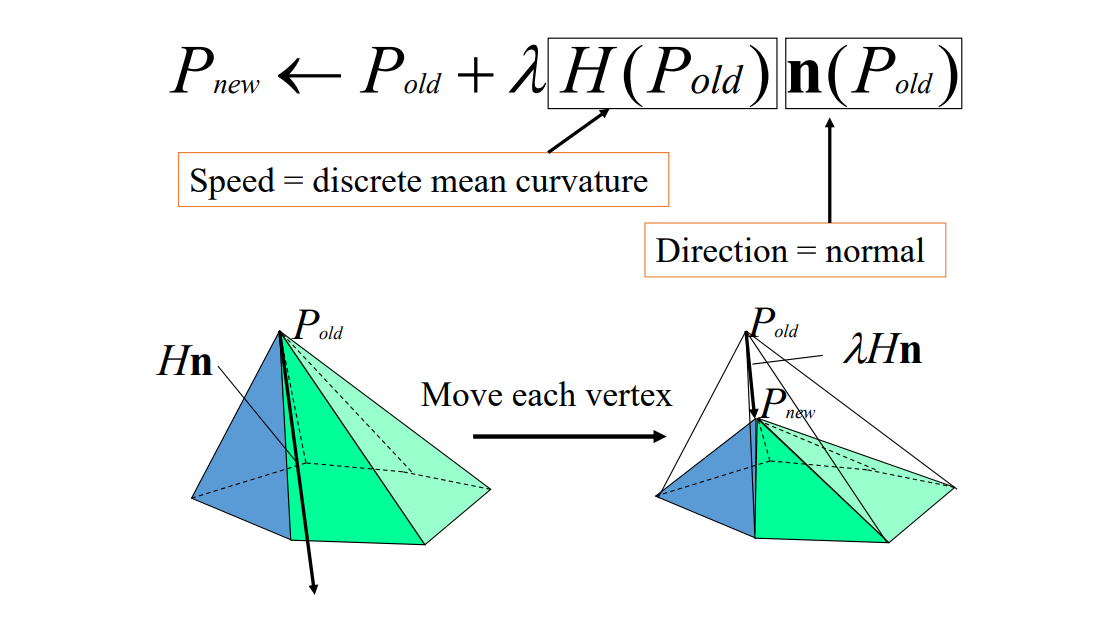
不断迭代，每个顶点都会接近平均曲率为0。（离散平均曲率流定理）

\(\lambda \)太大会不收敛。\(\lambda \)取小一点多走几步。

其中Hn的定义如下：

$$ H_n=\frac{\nabla_PA}{2A} $$

$$ H_n=\frac{1}{4A} \sum_{j}^{} (\cot \alpha _j+\cot \beta _j)(P-Q_j) $$

离散极小曲面的局部迭代法

非封闭曲面

找到边界 # 只能对非封闭曲面（带一条边界）操作    
固定边界顶点    
迭代 # 尝试试验不同的参数𝜆
   对每个内部顶点    
      找顶点1‐邻域    
      更新其坐标 # 更新坐标需要用老的顶点坐标   
更新所有顶点法向   

封闭曲面

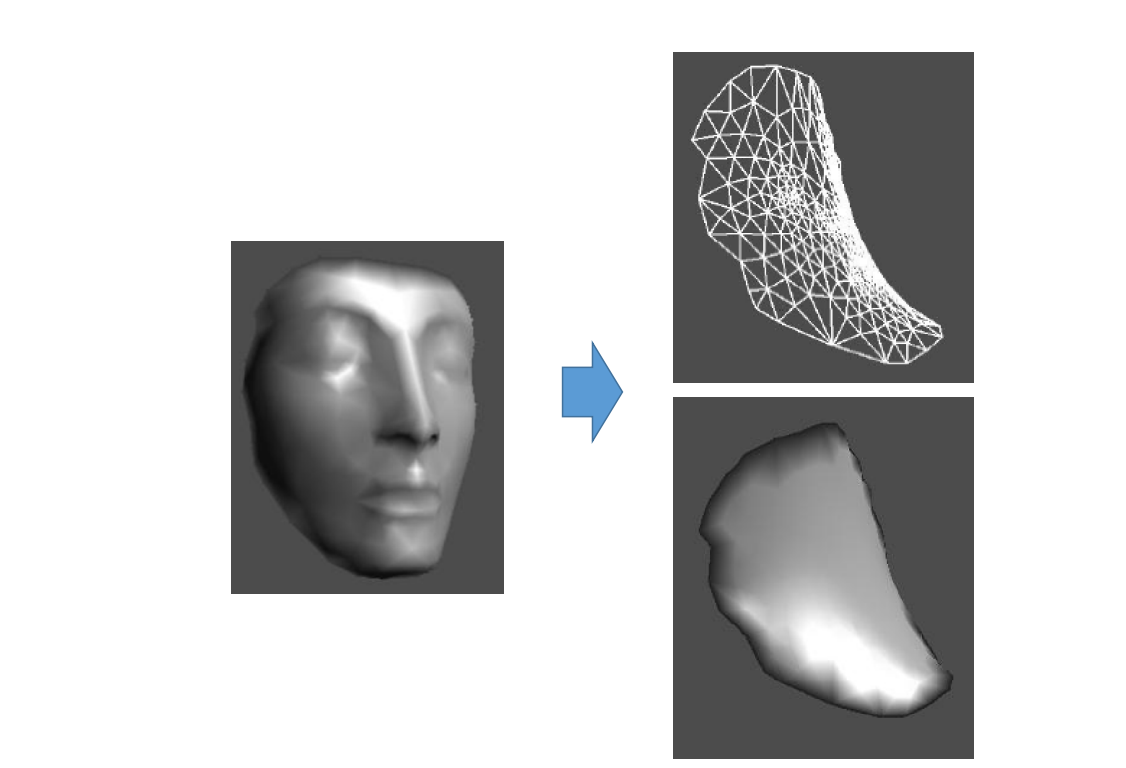
对于封闭曲面，不固定住的点，最后会收缩到一个点。

❓ 如何构造曲面边界？
答：自己构造

Triangle

http://www.cs.cmu.edu/~quake/triangle.html

当满足\(K=0时， L 的模长为0\)。
从任意取曲面优化成极小曲面的方法：

1. 计算出中间的黑点
2. 向黑点移动
   （重心）

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/