几何样条曲线

样条就是分段曲线的意思。

用分段Bezier曲线来插值型值点

给定型值点:
$$ k_0, \dots ,k_n\in \mathbb{R} ^3 $$

每两点间生成一段Bezier曲线，使得整体曲线满足一定的连续性\((𝐶^0,C^1,C^2)\)

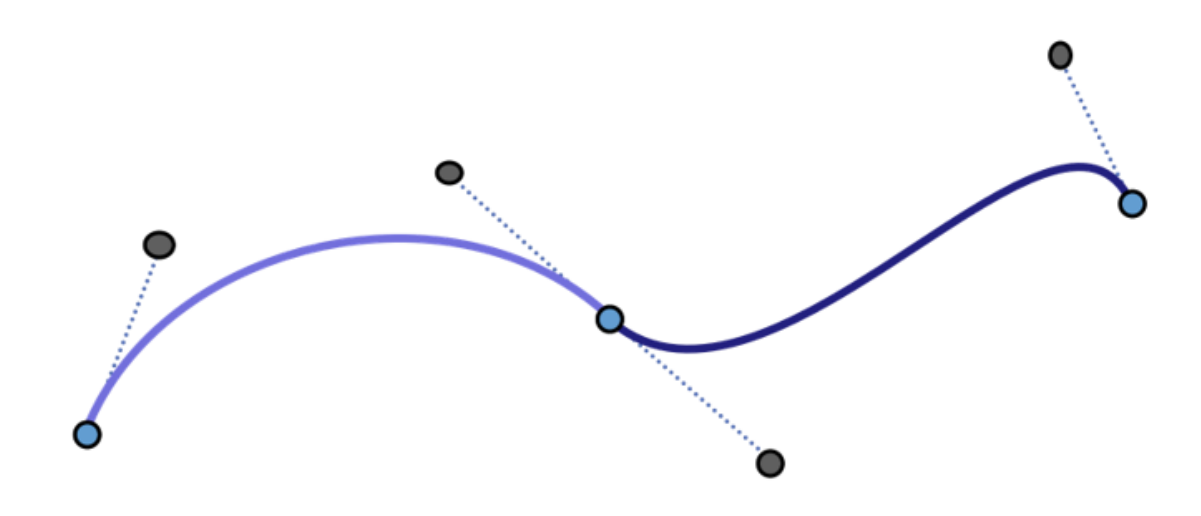
蓝点是型值点。黑色是为了控制生成的曲线额外添加的点。

两Bezier曲线的拼接条件

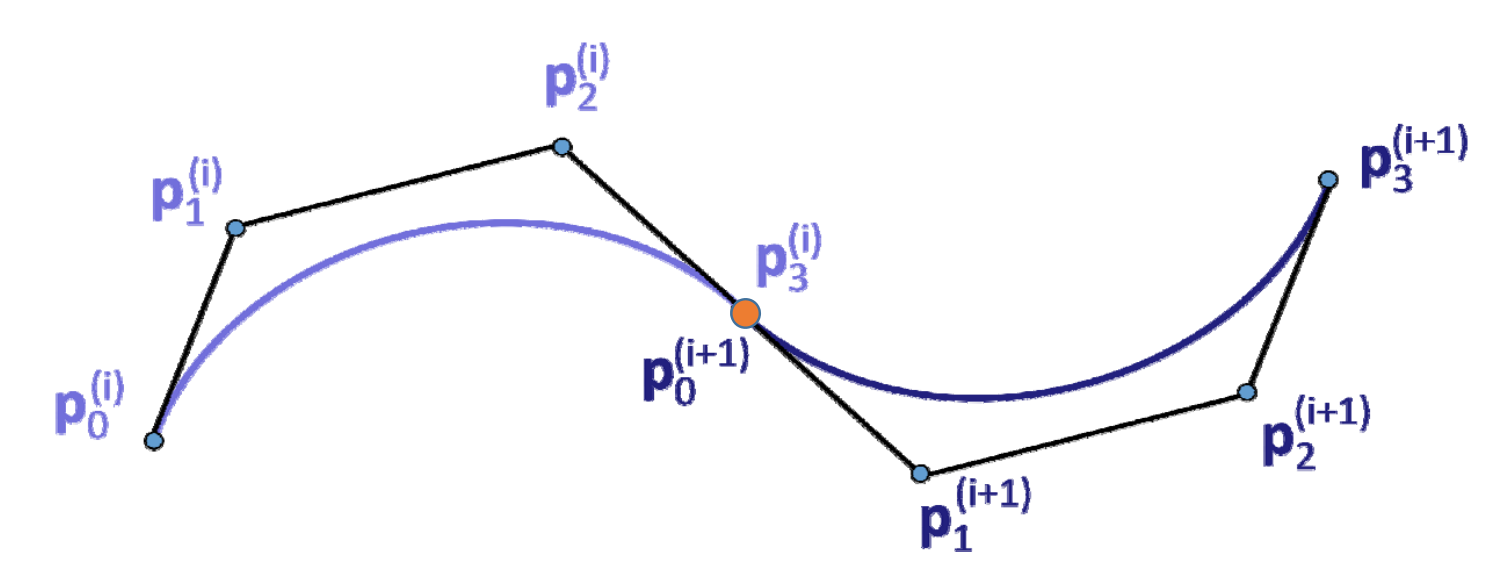
回顾：Bezier曲线的端点性质link

• C0连续与G0连续的条件：默认满足

• \(G^1\)连续：三点共线

• \(C^1\)连续：三点共线且等长

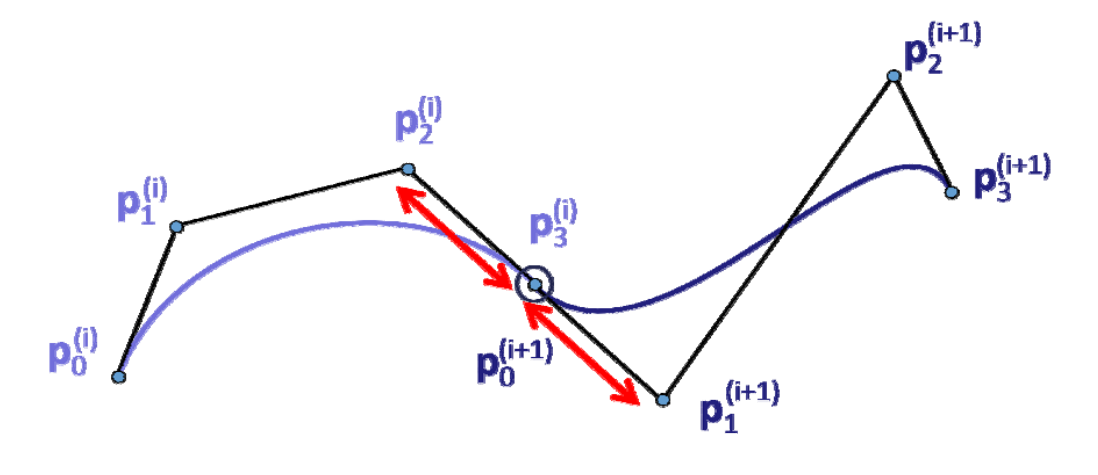
• \(C^2\)连续：\(𝑑^2⁄dt^2 \)为 \((p_2-2p_1+p_0),(p_n-2p_{n-1}+p_{n-2})\)，即阴影三角形相似
  

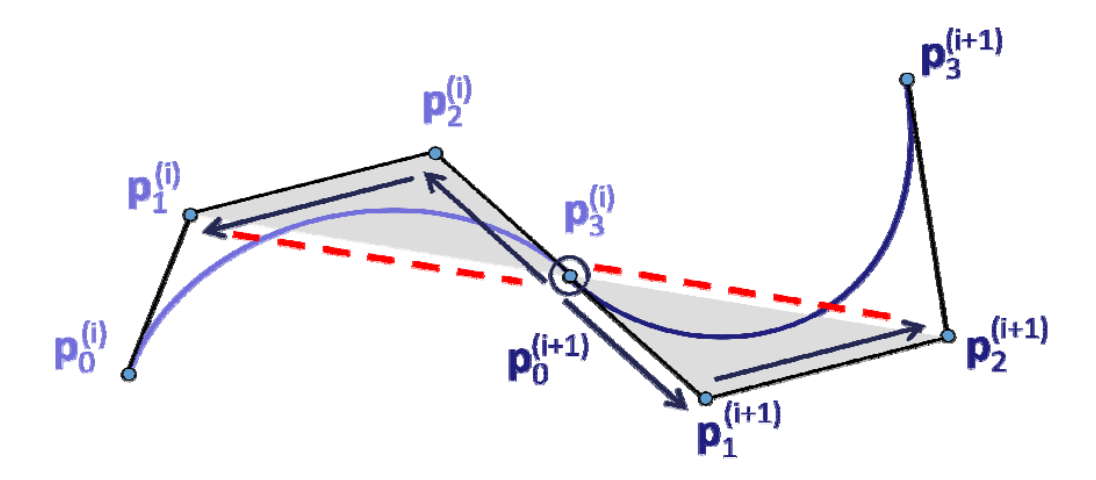
• \(G^2\)连续：？

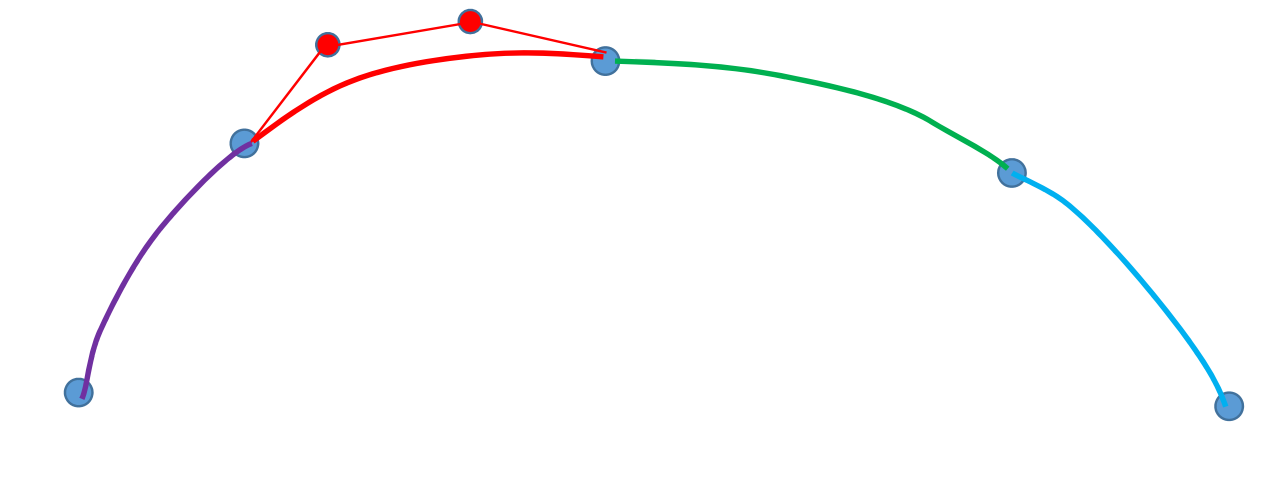
构造3次插值Bezier曲线的几何方法

用矩阵计算的方法

根据基构造矩阵，计算系数。
局限性，任意控制点的改变就要重新构造矩阵和计算

工程中常用的几何方法

构造曲线的关键是算出辅助控制点的位置。

[38:48]

(1) \(P_o 与P_2\)连线
(2) 过\(P_1点画与P_0P_2\)平行的线段，线段以\(P_1\)为中点，长度为\(P_0P_2的\frac{1}{6} \).
(3) 线段的端点是辅助控制点的位置。

这种方法能满足C1，不能满足C2

广义样条曲线

分段的多项式曲线（Bezier曲线）

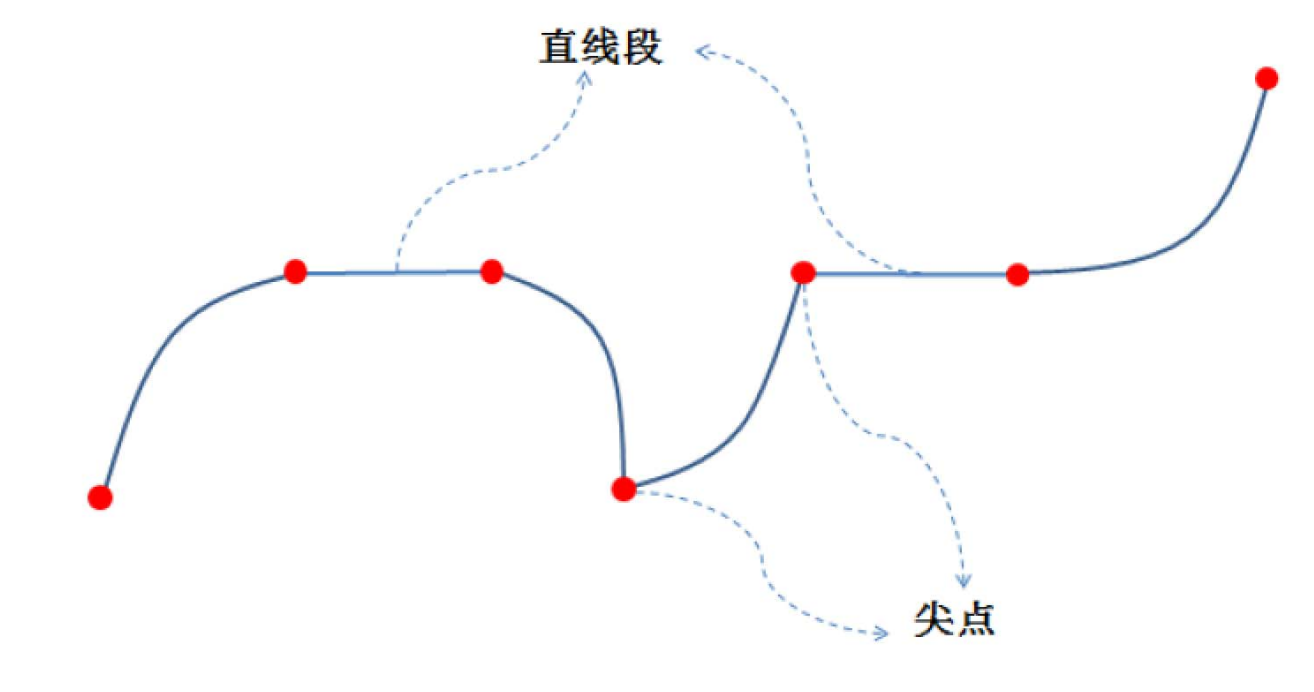
所有的分段连续曲线，曲线可以是直的，曲线之间也可以只有C1连续

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/