标准Gauss函数的变换

一般Gauss函数表达为标准Gauss函数的形式，即

$$ g_{0,1}(x) = \frac{1}{\sqrt{2\pi } } e^{-\frac{x^{2} }{2} } $$

把任意 Gauss 函数 \(g_{\mu,\sigma}(x)\)中的x做平移与缩放，使之成为 std Gauss 函数，即： $$ g_{\mu,\sigma}(x) \Rightarrow g_{0,1}(x') $$

$$ g_{\mu ,\sigma } (x)= \frac{1}{\sqrt{2\pi } } e^{-\frac{(x-\mu )^{2} }{2\sigma ^{2} } } =\frac{1}{\sqrt{2\pi } } e^{-\frac{1}{2}(\frac{x}{\sigma } -\frac{\mu }{\sigma } )^2} =g_{0,1 } (ax+b) $$

通过以上推导得：
$$ x'=ax+b $$

$$ a=\frac{1}{\sigma },b=\frac{\mu }{\sigma }
$$

RBF由各种不同的Gauss函数线性组合而成， 用这种变换形式来描述RBF函数：

$$ f(x)=b_{0}+\sum_{i=1}^{n} b_{i} g_{i}(x) $$

各种不同的Gauss基函数是由一个标准Gauss函数通过平移和伸缩变换而来的，因此RBF就可以写成这样：

$$ f(x)=\omega_{0}+\sum_{i=1}^{n} \omega_{i} g_{0,1}\left(a_{i} x+b_{i}\right) $$

换个方式看函数

神经网络

将Gauss函数看成网络

$$ f(x)=\omega_{0}+\sum_{i=1}^{n} \omega_{i} g_{0,1}\left(a_{i} x+b_{i}\right) $$

RBF函数可以画成这样：

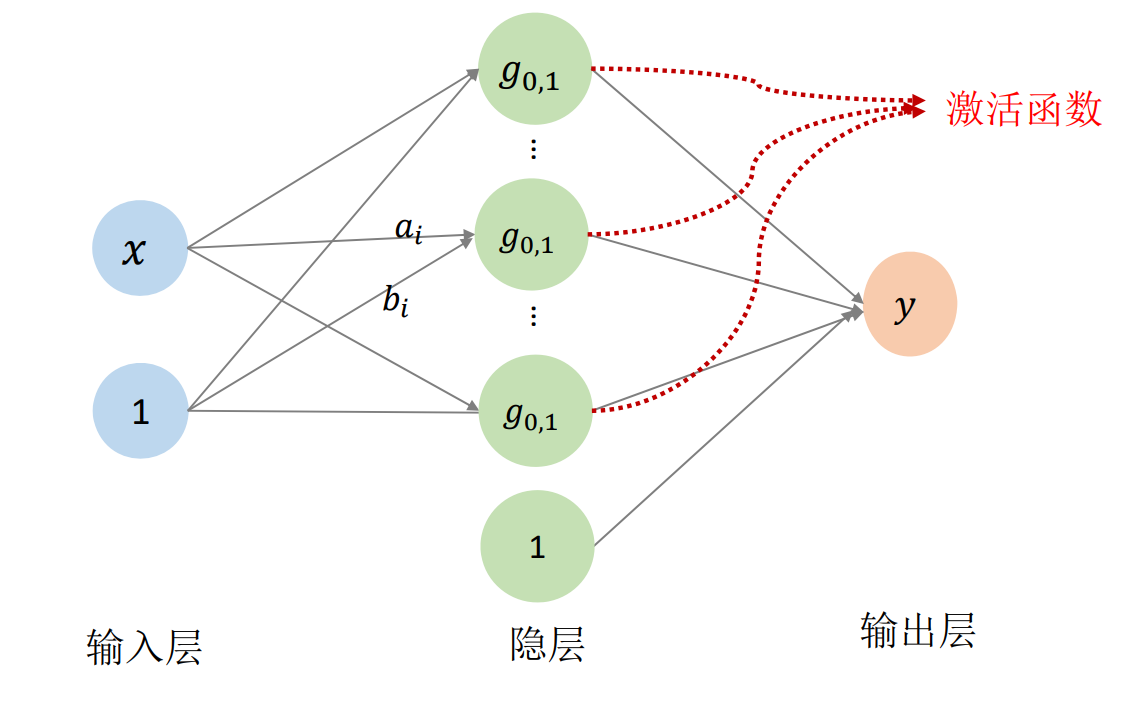
👆 [58:00] 用神经网络来描述RBF公式
✅ 其中\(\omega_0, \omega_i, a_i, b_i\)都是待优化的函数。 当n足够多时，f(x)可以逼近任何函数。
\(x\) 本身一维，考虑到平移，再升一维。隐层的1是指基函数线性组合后整体增加一个平移。
在这里， std gauss 相当于激活函数。连接线上的数值 \((a_i,b_i,\omega _i)\)是网络参数。\(n\)对应网络隐层的结点个数，需要手调。

神经元

一个神经网络就是一个函数

💡 从传统机器学习到神经网络，这是我见过的最好的解释。
✅ 参数的初值很重要，最好能根据物理意义找到初值。

RBF 神经网络

RBF (Radial Basis Function)，径向基函数，是高维的高斯函数。

RBF 神经网络的问题是，关于 \(a,b\) 的导数难求，高阶且非凸， 难以优化。只能找局部最小，因此初值很重要。

核函数思想

没解释

Gauss函数的特性：拟局部性

没解释

Guass拟合函数的进化

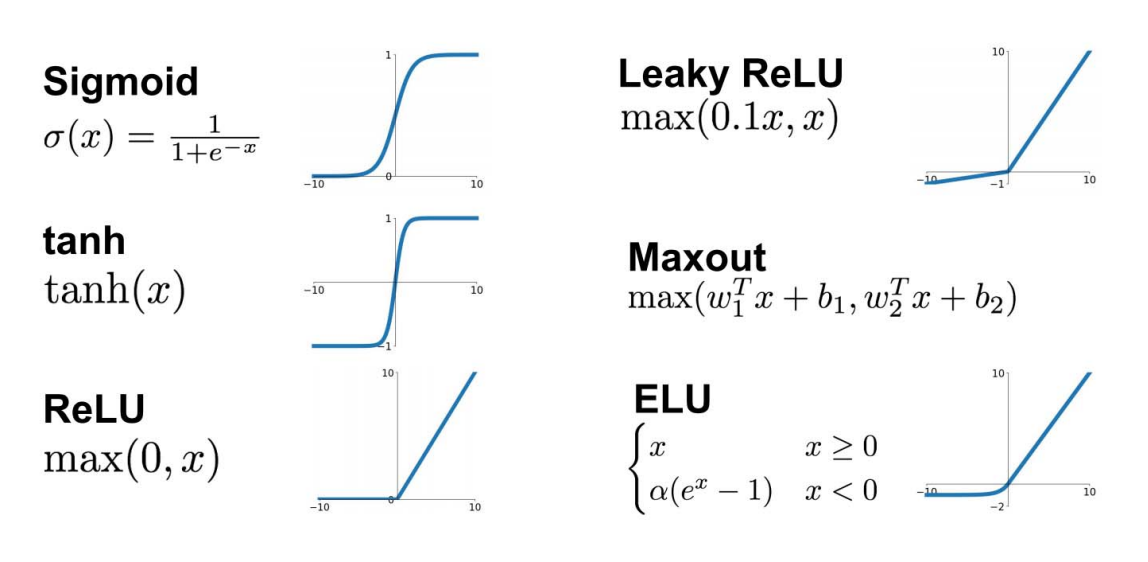
激活函数的选择？

启发：由一个简单的函数通过（仿射）变换构造出一组基函数，张成一个函数空间

关键是基函数的表达能力是否足够强：是否完备/稠密的？

机器学习的本质是在做拟合。

高维情形：多元函数

🔎 见【多元函数】，link

变量的多个分量的线性组合

$$ (x_1,x_2,...,x_n)\longrightarrow g_{0,1}(a^i_1x_1+a^i_2x_2+...+a^i_nx_n+b_i) $$

单隐层神经网络函数：

$$ f(x_1,x_2,...,x_n) = \omega_{0}+\sum_{i=1}^{n} \omega_{i} g_{0,1}(a^i_1x_1+a^i_2x_2+...+a^i_nx_n+b_i) $$

高维只是在输入层，输出层纵向多加几个圈
共享基函数，使用不同的系数

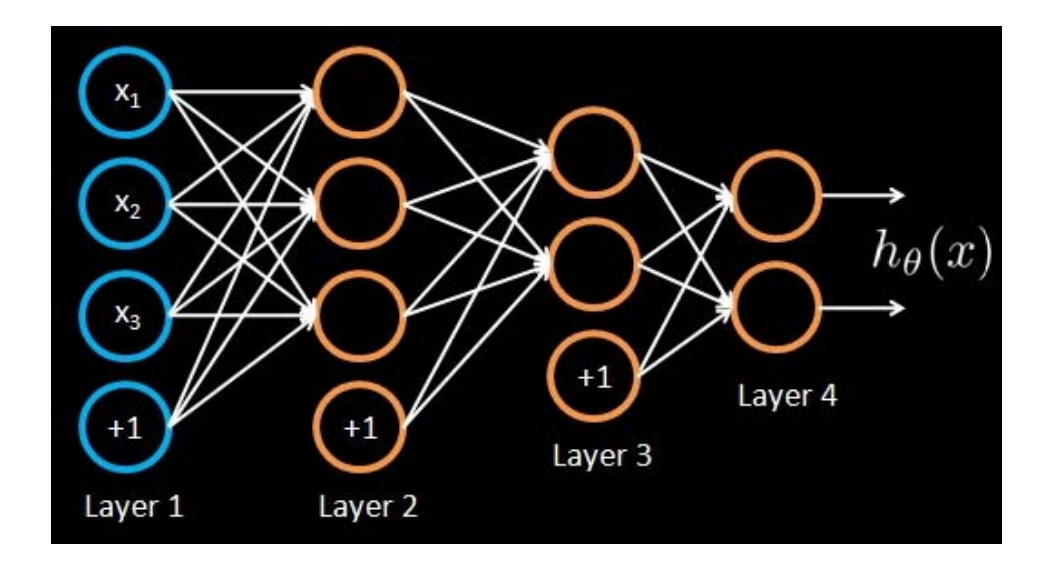
多层神经网络：多重复合的函数

线性函数和非线性函数的多重复合

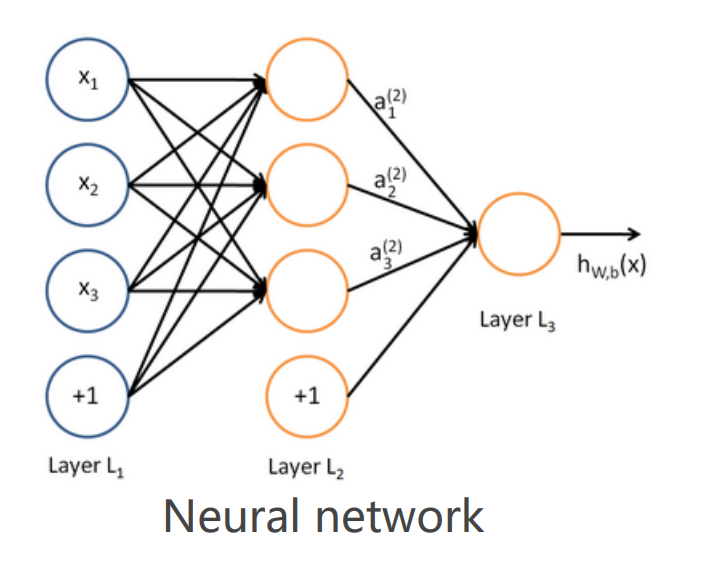
$$ a_1^{(2)}=f(W_{11}^{(1)} x_1+W_{12}^{(1)}x_2+W_{13}^{(1)} x_3+b_1^{(1)}) $$

$$ a_2^{(2)}=f(W_{21}^{(1)} x_1+W_{22}^{(1)} x_2+W_{23}^{(1)} x_{3}+b_{2}^{(1)}) $$

$$ a_{3}^{(2)}=f(W_{31}^{(1)} x_{1}+W_{32}^{(1)} x_{2}+W_{33}^{(1)} x_{3}+b_{3}^{(1)}) $$

$$ h_{W, b}(x) =a_{1}^{(3)}=f(W_{11}^{(2)} a_{1}^{(2)}+W_{12}^{(2)} a_{2}^{(2)}+W_{13}^{(2)} a_{3}^{(2)}+b_{1}^{(2)}) $$

通常每层使用相同的激活函数，方便优化
增加网络的深度和宽度，都会极大膨胀参数个数
同样参数量级下，通常深的比宽的好，因为深的自由度更高

用神经网络函数来拟合数据

Regression problem
Input: Given training set \((x_1,y_1), (x_2,y_2),(x_3, y_3)\),….
Output: Adjust parameters \(0\)(for every node)to make: $$ h(x_i)\approx y_i $$

$$ F(X)=\sum_{i=1}^{N} v_i\varphi (W^T_iX+b_i) $$

❓ Why it works?
答：只要网络足够大，参数足够大，就能逼近任意函数。

❗ 存在的问题 与传统拟合一样存在同样的问题： 函数个数如何选？!
调参！

使用深度学习的方法

问题建模：理解问题、问题分解（多个映射级联）…

• 找哪个？
  • 损失函数、各种Penalty、正则项…
• 到哪找？
  • 神经网络函数、网络简化…
• 怎么找？
  • 优化方法（BP方法）
  • 初始值、参数…

调参：有耐心、有直觉…

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/