为什么逼近？

用逼近代替插值的优点：
• 数据点含噪声、outliers等
• 更紧凑的表达
• 计算简单、更稳定

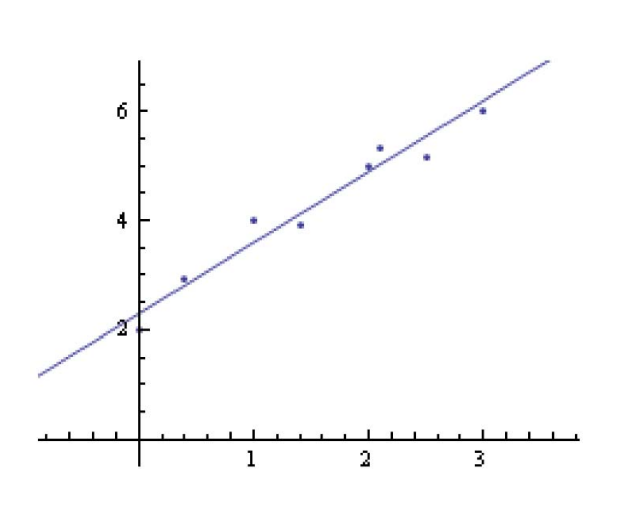
逼近问题

给定一组线性无关的连续函数集合$B$={$b_1, \ldots b_n$}和一组结点{$(x_1, y_1)$, ...,$(x_m, y_m)$}, 其中$m>n$。
在$B$张成空间中哪个函数$f\in\operatorname{span}(B)$对结点逼近最好?

🔎 [31：38]

最佳逼近

最小二乘逼近

$$\underset{f \in \operatorname{span}(B)}{\operatorname{argmin}} \sum_{j=1}^{m}\left(f\left(x_{j}\right)-y_{j}\right)^{2}$$

公式是关于系数$(\lambda _1,\lambda _2,\dots ,\lambda _n,)$的函数，直接求极小值的闭式解。

$$\sum_{j=1}^{m}\left(f\left(x_{j}\right)-y_{j}\right)^{2}=\sum_{j=1}^{m}\left(\sum_{i=1}^{n} \lambda_{i} b_{i}\left(x_{j}\right)-y_{j}\right)^{2}$$

$$=(M \lambda-y)^{T}(M \lambda-y)$$

$$=\lambda^{T} M^{T} M \lambda-y^{T} M \lambda-\lambda^{T} M^{T} y+y^{T} y$$

$$=\lambda^{T} M^{T} M \lambda-2y^{T} M\lambda +y^{T} y$$

$$M=\left(\begin{array}{ccc} b_{1}\left(x_{1}\right) & \ldots & b_{n}\left(x_{1}\right) \\ \ldots & \ldots & \ldots \\ b_{1}\left(x_{m}\right) & \ldots & b_{n}\left(x_{m}\right) \end{array}\right)$$

求解

上页公式可转化为关于$\lambda$的二次多项式
$$\lambda^{T} M^{T} M \lambda-2 y^{T} M \lambda+y^{T} y$$

求公式的法方程，可得使公式达到最小值，其解应满足：

$$M^{T} M \lambda=M^{T} \mathrm{y}$$

提示
－ 最小化二次目标函数$x^TAx+b^Tx+c$
－ 充分必要条件:$2Ax=-b$

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/