两种观点，两种表达方式

使用幂基来表达曲线

二次多项式曲线（抛物线）:

$$ 𝑓(t)=at^2+bt+c $$

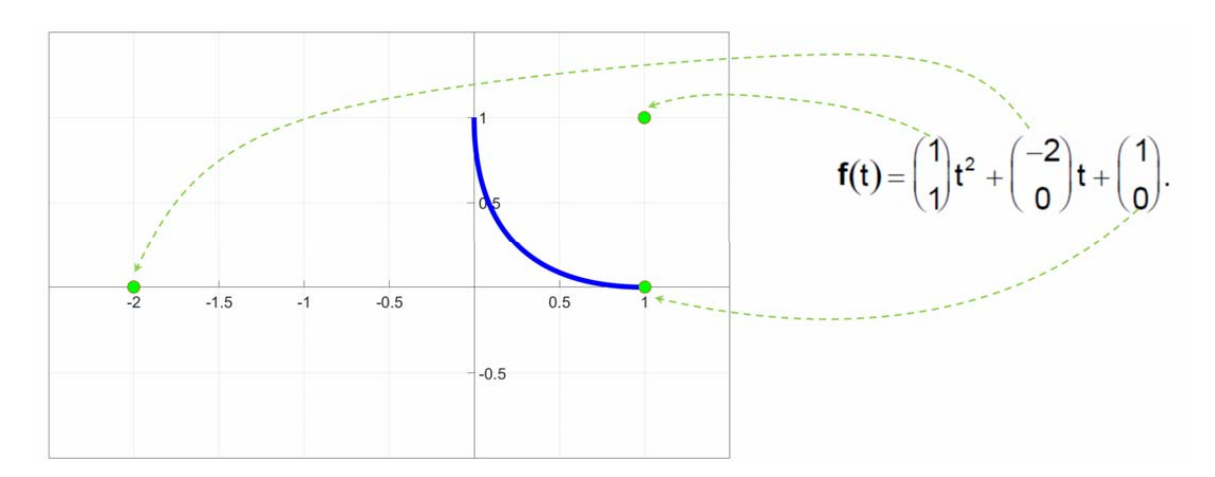
几何观点：基函数为这些顶点的组合权系数。

从几何观点来看，系数顶点与曲线本身无直观的联系，因此无几何意义！ 不利于用户来交互修改曲线：适用于重建，但不适用于设计

使用Bernstein基函数表达

使用Bernstein基函数来改写

$$ f(t)=\binom{1}{1} t^2+\binom{-2}{0} t+\binom{1}{0} $$

$$ \downarrow $$

$$ f(t)=\binom{1}{0} (1-t)^2+\binom{0}{0} 2t(1-t)+\binom{0}{1} t^2 $$

系数顶点与曲线关联性强，具有很好的几何意义。对于交互式曲线设计更观

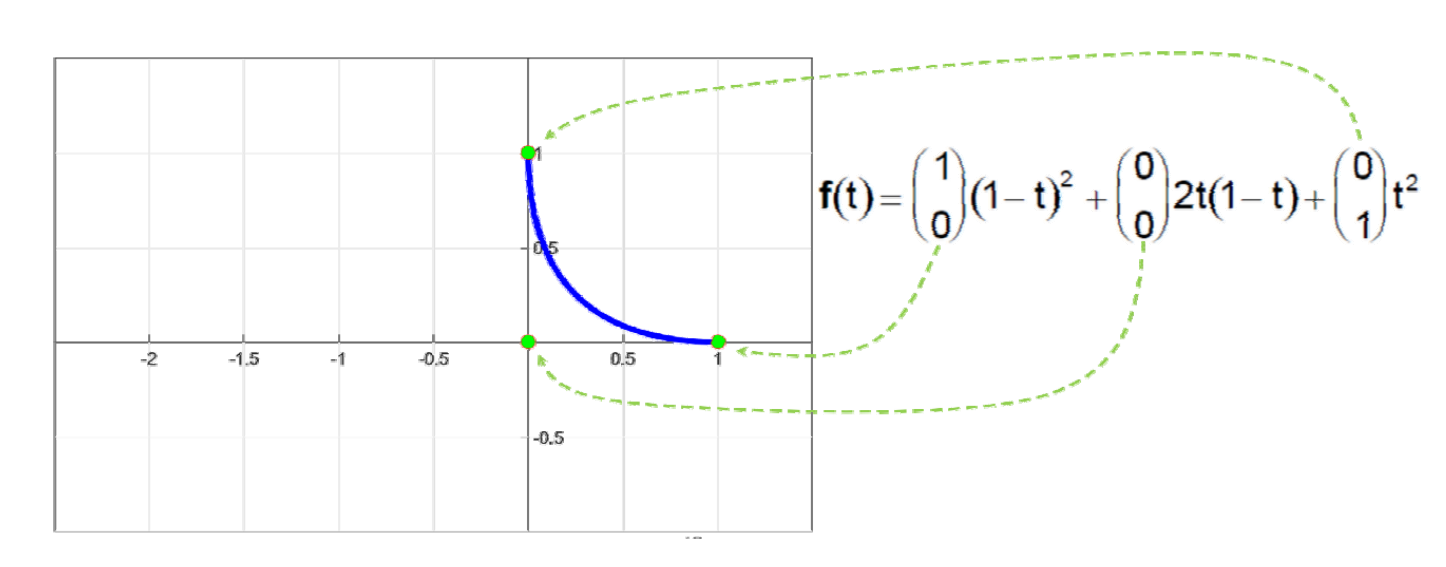
用Bernstein基函数所表达的曲线具有非常好的几何意义！

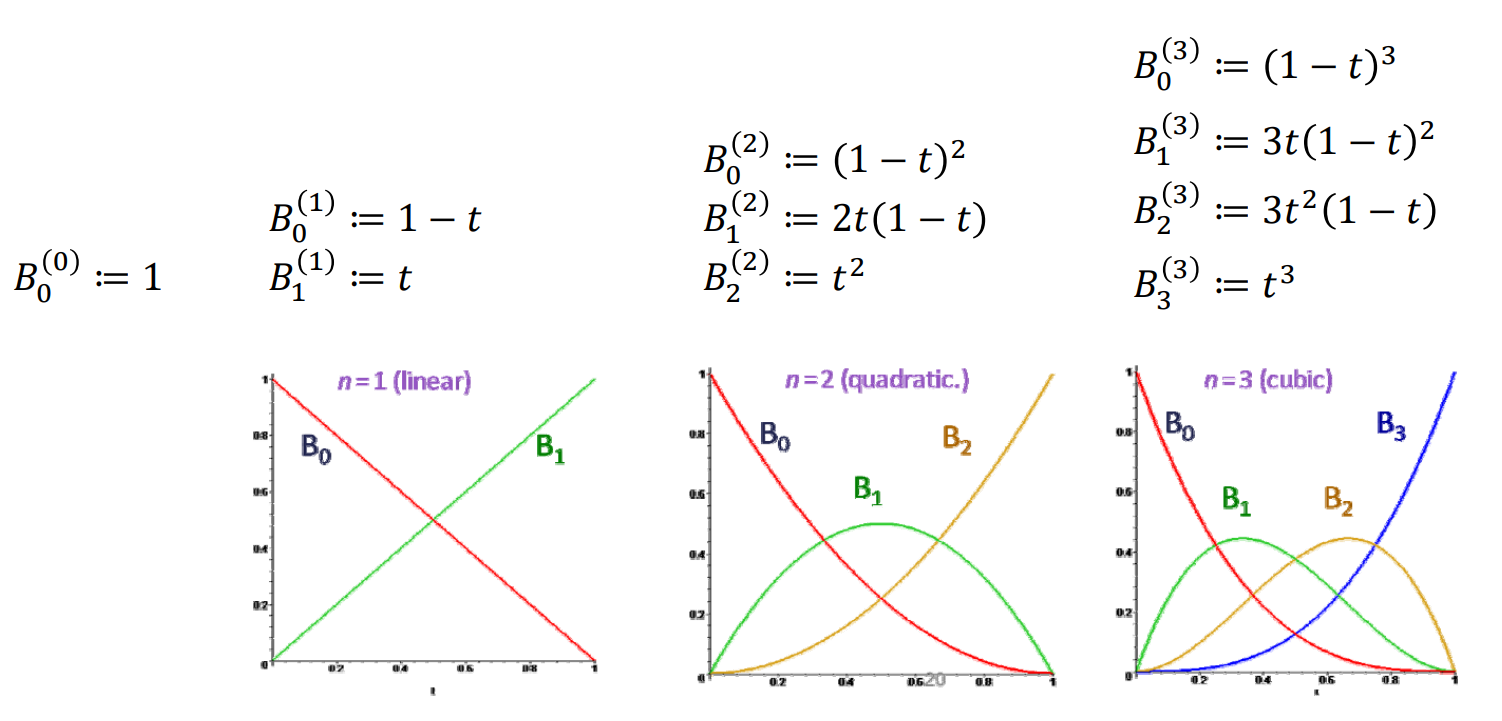
Bernstein基函数

\(n\)次Bernstein基函数:\(B=\){\(B_0^{(n)},B_1^{(n)},\cdots ,B_n^{(n)}\)}

$$ B_i^{(n)}(t)=\binom{n}{i}t^i(1-t)^{n-i}=B_{i-th basis function}^{(degree)} $$

where the binomial coefficients are given by: $$ \binom{n}{i}= \begin{cases} \frac{n!}{(n-i)!i!} && for \quad 0\le i\le n \\ 0 && otherwise \end{cases} $$

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/