假定:仅函数形式
假定:仅函数形式,一般曲线(非函数形式)后面再学习
函数形式是指:
$$ f:R^1 \rightarrow R^1 $$
或
$$ y=f(x) $$
🔎 [03:55]
✅ 曲线中每个x都对应一个\(y\)值,是函数函数形式的曲线。上面的公式是函数形式曲线的两种表达方式。
✅ 这三个曲线是一般曲线
函数拟合问题
输入: 一些观察 (采样) 的数据点\((x_i,y_i)\)
输出: 拟合数据点的函数\(y=f(x)\), 并用于预测
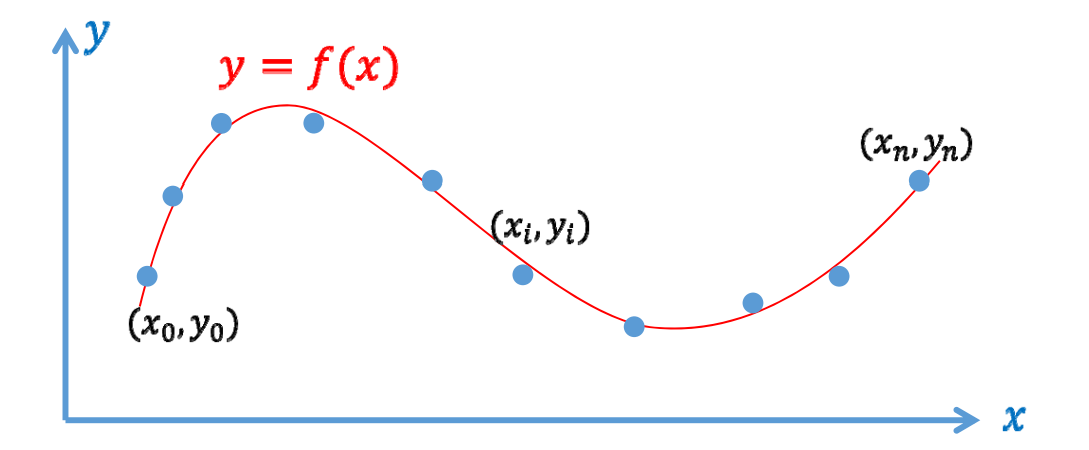
函数拟合的目的:
- 压缩:把大量采样点压缩成函数
- 预测:预测未采样的点
这种拟合函数有多少个?怎样判断拟合函数的“好坏”?
🔎 [06:01]
方式一:分段线性
🔎 [06:12]
数据误差为\(0\),但函数性质不够好:只有\(C^0\)连续,不光滑(数值计算)
✅ \(C^0\)连续不可求导,会给后面的使用带来难度。
离散几何研究这种函数,以目前的角度来看函数不好。
方式二:光滑插值
🔎 [08:06]
数据误差为\(0\),但可能被 “差数据” (噪声、outliers) 带歪, 导致函数性质不好、预测不可靠
方式三:逼近拟合
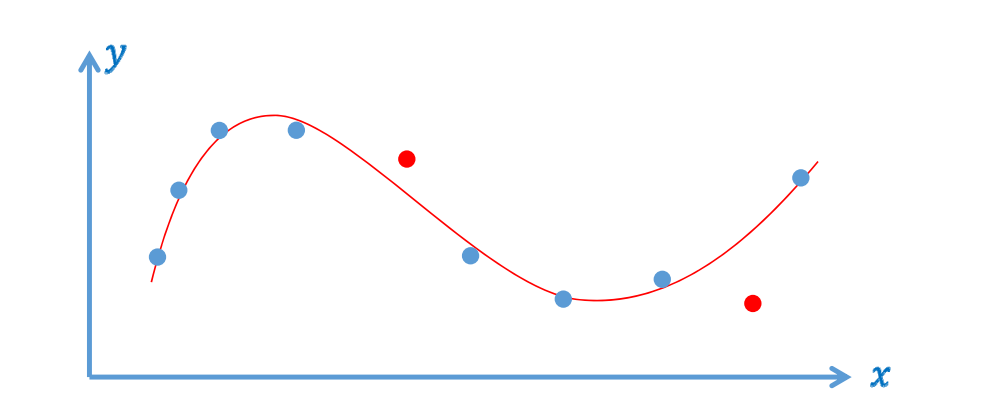
🔎 [09:48]
允许误差不为\(0\),但要足够小,这样能抵抗噪声
求拟合函数的应用驱动
大部分的实际应用问题
- 可建模为:找一个映射/变换/函数
- 输入不一样、变量不一样、维数不一样
求函数拟合一定要考虑应用背景,要有针对性地设计函数空间,否则只能靠试,就会很难了。
三步曲方法论
🔎 [12:50]
到哪找?
确定函数的表达形式 (函数集、空间),一般是由基函数所张成的线性空间
(1)确定某个函数集合(“池子”)
(2)具有某种结构容易表达(比如线性函数空间)
(3)尽量广泛(表达能力强)
$$ L=span(b_0(x),\dots b_n(x)) $$
待定基函数的组合系数 (求解变量)
$$ f_\lambda (x)=\sum_{k=0}^{n} \lambda_ib_i(x) $$
\(f\)由待定系数\(\lambda=\left (\begin{array}{c} \lambda_{1} \\ \ldots \\ \lambda_{n} \end{array}\right) \)确定
通常把求一个函数转化为一组系数的求解。
基函数的选择决定了函数空间能拟合怎样的函数。
找哪个?
度量哪个函数是好的/“最好”的
定义损失函数,包括数据误差项(逼近数据的度量)与正则项(对函数性质的度量)
能量项 = 误差项 - 正则项
正则项:对系数加约束就相当于对函数加约束。
统计模型、规划模型...
怎么找?
-
线性问题
线性问题,可转化为解线性方程或线性方程组的问题,例如:
求解误差函数的驻点 (导数为 \(0 \)之处),并转化为系数的方程组
如果是欠定的 (有无穷多解),则修正模型,例如改进/增加各种正则项:Lasso、岭回归、稀疏正则项… -
非线性问题:
- 凸问题:有理论保证
- 非凸问题:难!数值求解( 梯度下降法、牛顿法、拟牛顿法、L‐BFGS, … ),须选择合适初值、步长等;一般要根据具体的优化问题形式及特点来设计合适的优化方法!
本文出自CaterpillarStudyGroup,转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/