算法描述

Input: points $𝒃_0,𝒃_1,\dots 𝒃_n∈ \mathbb{R} ^3$
Output: curve $x(t),t∈ [0,1]$

过程示例

Repeated convex combination of control points

$$b_i^{(r)}=(1-t)b_i^{(r-1)}+tb_{i+1}^{(r-1)}$$

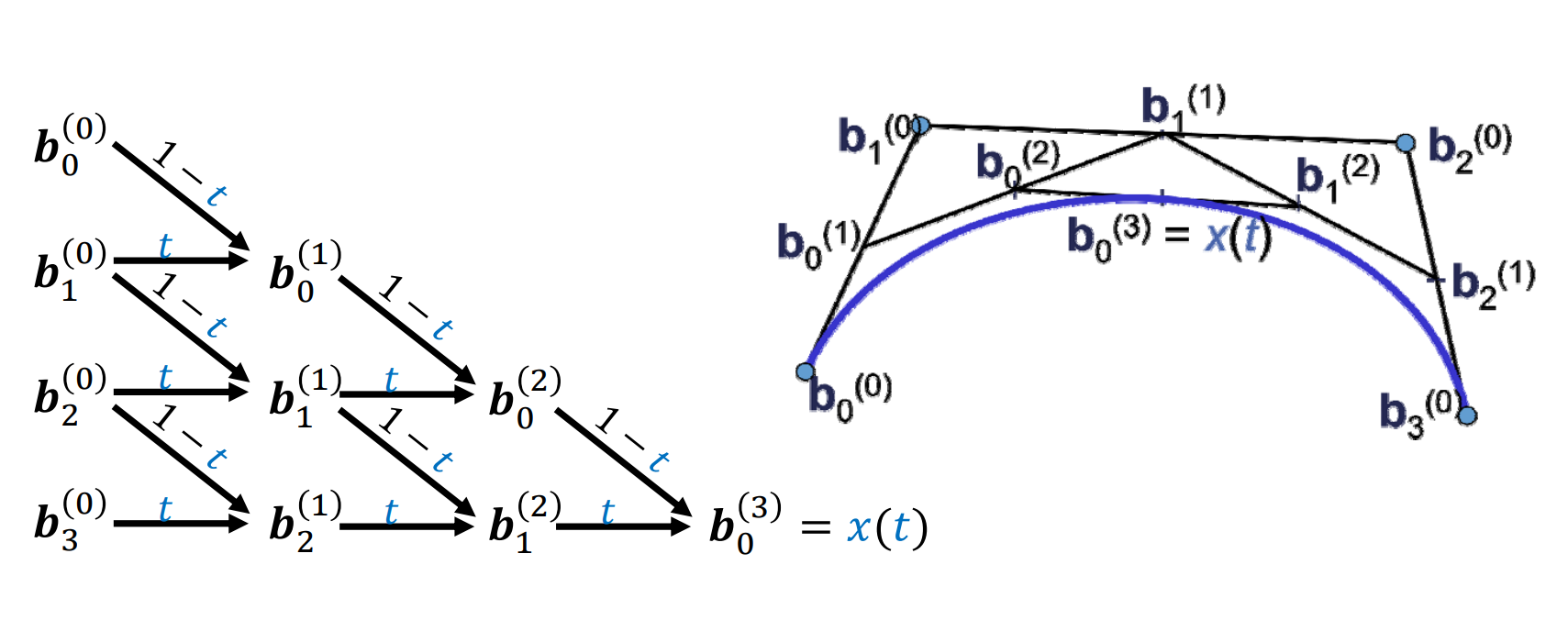
点 $b_0^{(0)},b_0^{(1)},b_0^{(2)},b_0^{(3)}是曲线 b_0^{(0)},b_0^{(3)}$的控制点。

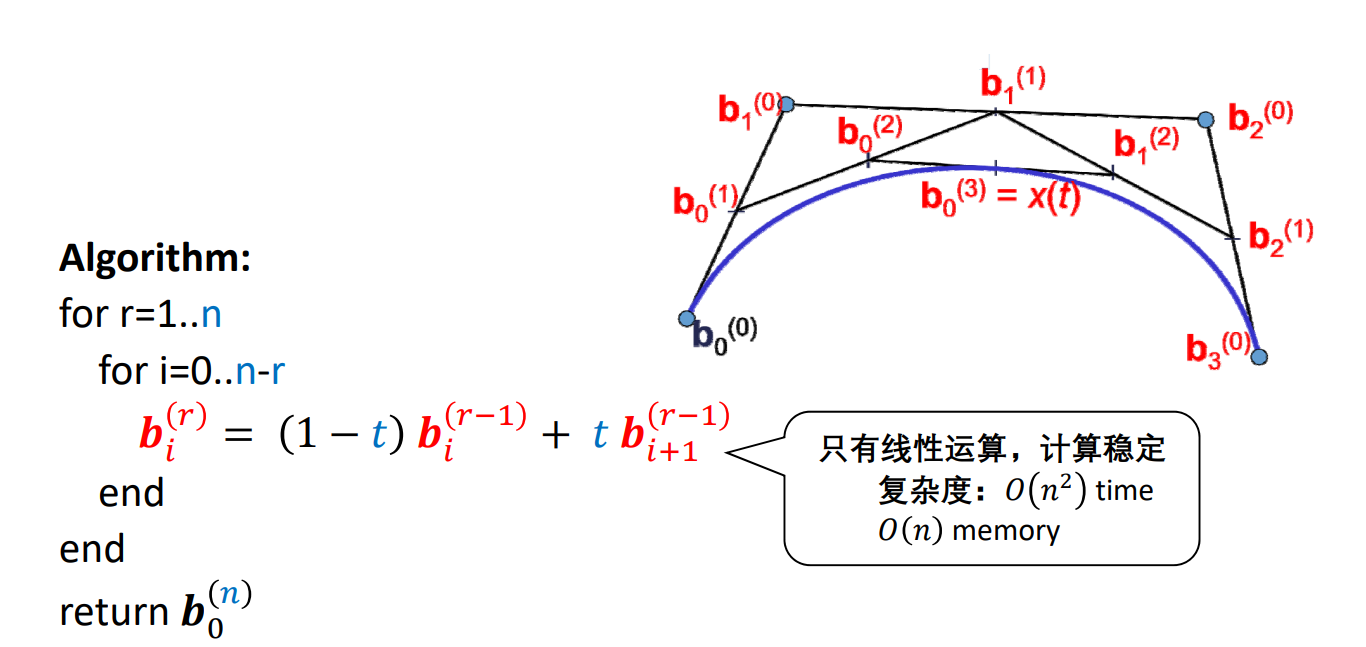
例子

给定3个点，画Bezier曲线

把起点看作是t=0时刻，终点看作是t=1时刻，画Bezier曲线，相当于求t=[0,1]区间时pt所在的位置。把范围所有时刻的pt连起来就是Bezier曲线。

1. 算出b0b1中的t位置的点为$b^1_0$
2. 算出b1b2中的t位置的点为$b^1_1$
3. ab连成一条线，算是ab中的t位置的点为$b^2_0$
4. $b^2_0$是 Pt 的位置，

给定4个点，画Bezier曲线

[23:24]

总结

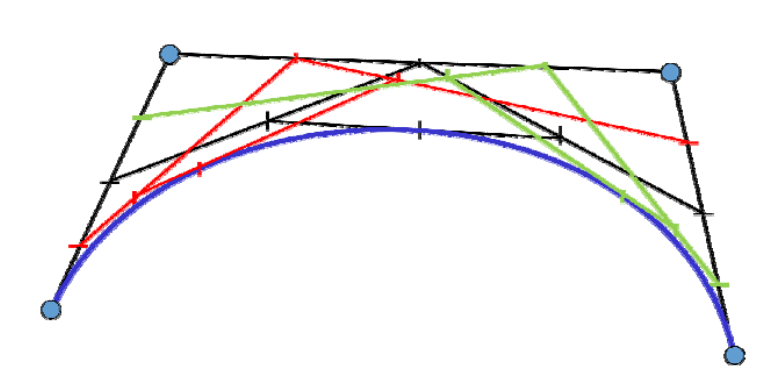
• 给定$t$，计算Bezier曲线$x(t)$上参数为$t$的点

[30:18]局限性：一次只能针对一个$t$值计算。

• 良好的几何意义：该点将曲线一分两条子Bezier 曲线，其控制顶点是中间生成的点
• 可用于Bezier曲线的离散及求根等许多应用

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/