曲线的几何连续性
参数连续性
定义
在数学分析/高等数学中,我们所说的“连续性”(光滑性)是指“参数连续性”:
给定两条曲线\(x_1(t)\)和\(x_2(t)\),其中\(x_1(t)\)定义在\([t_0,t_1]\),\(x_2(t)\)定义在\([t_1,t_2]\)
曲线\(𝒙_1\)和\(𝒙_2\)在\(t_1\)称为\(C^r\)连续的,如果它们的从\(0^{th}\)(\(0\)阶) 至\(r^{th}\)(\(𝑟\)阶)的导数向量在\(𝑡_1\)处完全相同。
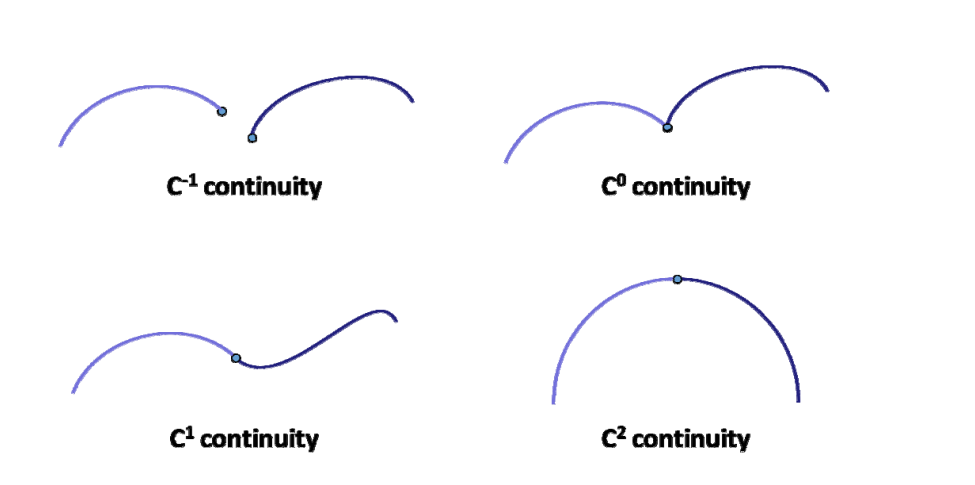
- \(C^{-1}\):表示不连续
- \(C^0\): position varies continuously
- \(C^1\): First derivative is continuous across junction。即 the velocity vector remains the same
- \(C^2\): Second derivative is continuous across junction 即 The acceleration vector remains the same
参数连续性的不足
参数连续性过于严格,在几何设计中不太直观
• 例子1:一条线段v0v1
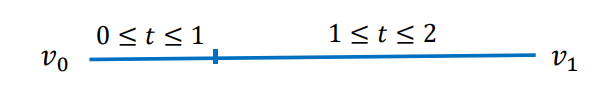
表示为分段函数:
$$ \varphi(t)=\begin{cases} v_{0}+\frac{v_{1}-v_{0}}{3} t, 0 \leq t \leq 1\\ v_{0}+\frac{v_{1}-v_{0}}{3}+\frac{2\left(v_{1}-v_{0}\right)}{3}(t-1), 1 \leq t \leq 2 \end{cases} $$
线段上的任意点应该是处处连续的。但是, $$ {\varphi }'(1-)=\frac{v_{1}-v_{0}}{3},{\varphi }' (1+)=\frac{2(v_{1}-v_{0})}{3} $$
\(\varphi (t)\)在\(t=1\)的左右导数不相等,因此,\(\varphi(t)\)在\([0,2]\)中不是\(C^1\)的,与直线的连续性应是\(C^\propto\)的矛盾。
❓ 问:为什么此时在\(t=1处 C^{1}\)不连续
答:导数反应的是对变量的变化率,而图中两段的\(t\)是不同的变量。
因此,参数连续性依赖于参数的选择,同一条曲线,参数不同,连续阶也不同。
• 例子2:同一条线段,但对参数化方法做一些改造:
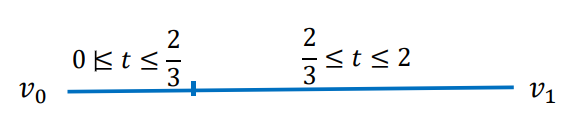
表示为分段函数:
$$ \varphi(t)=\begin{cases} v_{0}+\frac{v_{1}-v_{0}}{3} t, 0 \leq t \leq \frac{2}{3}\\ v_{0}+\frac{v_{1}-v_{0}}{3}+\frac{\left(v_{1}-v_{0}\right)}{3}(t-\frac{2}{3}), \frac{2}{3} \leq t \leq 2 \end{cases} $$
则\({\varphi }' (\frac{2}{3}- )={\varphi }' (\frac{2}{3}+ ),\varphi (t)\)在\([0,2]\)就是\(C^\infty \)了。
这个参数化方法的改造,本质是引入了参数的一个变换
$$ t=\begin{cases} \frac{2}{3}s,0\le s\le \frac{2}{3},\\ \frac{3}{4}(s-\frac{2}{3})+1,\frac{2}{3}\le s\le 2. \end{cases} $$
使得原来不是\(C^1 \)的曲线变为\(C^1 \)的了。
参数连续性依赖于参数定义,无法刻画曲线本征的特性。因此引入几何连续性。
几何连续性
定义
设\(\varphi (t)(a\le t\le b)\)是给定的曲线。若存在一个参数变换\( t=p(s)(a_1\le s\le b_1)\), 使得\(\varphi (p(s))\in C^n[a_1,b_1]\),且\(\frac{d\varphi (p(s))}{ds} \ne 0\), 则称曲线\(\varphi (t)(a\le t\le b)\)是\(n\)阶几何连续的曲线,记为 $$ \varphi (t)\in GC^n[a,b] $$
或
$$ \varphi (t)\in G^n[a,b] $$
把线段\(C^1\)不连续变成\(C^\infty \)连续的过程就是参数变换的例子。这里只是给出定义,不提供参数变换的方法。
性质
- 条件 \(\frac{d\varphi (p(s))}{ds} \ne 0\)保证了曲线上无奇点;
一般不考虑有奇点的情况
- 几何连续性与参数选取无关,是曲线本身固有的几何性质;
本征特征:不会由于曲的旋转、平移而改变的特征,例如曲率。
- \(𝐺^n\) 的条件比\(𝐺^n\)的宽,曲线类型更多;
具体形式
• \(𝐺^0\):表示两曲线有公共的连接端点,\(C^0\)与的条件一致
• \(𝐺^1\):两曲线在连接点处有公共的切线方向,即切线方向连续,切线长度可以不同。
• \(𝐺^2\):两曲线在连接点处有公共的曲率圆,即曲率连续
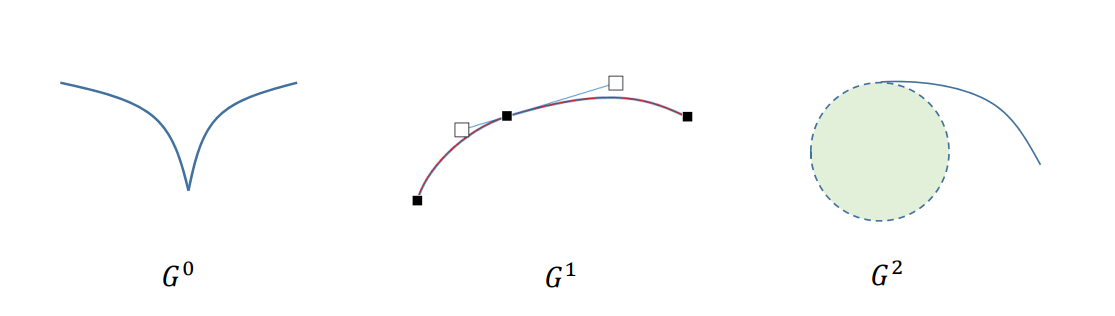
曲线编辑工具。跳过
两种连续性的比较
C连续适合于动画。G连续适合于设计建模。
本文出自CaterpillarStudyGroup,转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/