Bernstein基函数的性质

🔎 定义见上一页

对称性

$$ B_i^{(n)}(t)=B_{n-i}^{n}(1-t) $$

且

\(B^{(n)}_i(t)\) 在\(t= \frac{i}{n} \)达到最大值

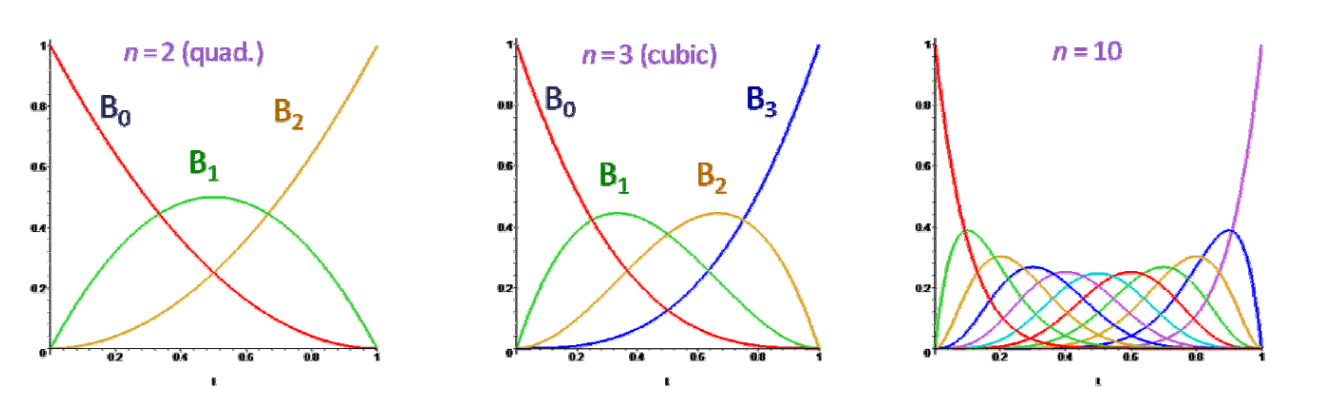
正权性

正性（非负性）+ 权性 = 凸包性

$$ B_i^{(n)}(t)\ge 0,\forall t\in [0,1] $$

$$ \sum_{i=1}^{n}B_i^{(n)}(t)=1, \forall t\in [0,1] $$

基性

\(B=\){\(B_0^{(n)},B_1^{(n)},...,B_N^{(n)}\)}是次数不高于n的多项式集合（空间）的一组基

且与幂基可以相互线性表达：

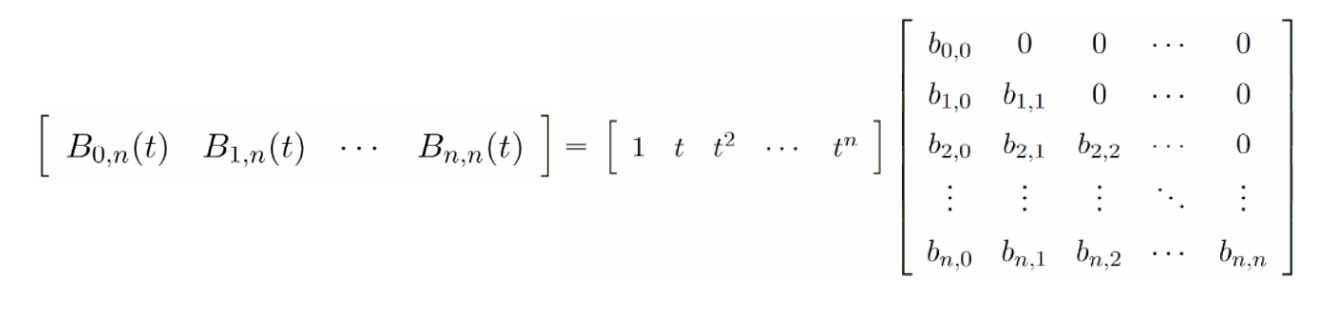
递推公式

基函数的递推公式

$$ B_i^{(n)}(t)=（1-t）B_i^{(n-1)}(t)+tB_{i-1}^{(n-1)}(1-t) $$

with \( \quad B_0^{(0)}(t)=1，B_i^n(t)=0\) for \(i\notin \){\(0\cdots n\)}

由 \(\binom{n-1}{i} +\binom{n-1}{i-1}=\binom{n}{i} \)可推导得到

\(n\)阶的基函数由2个\(n-1\)阶的基函数加权得到，利于保持一些良好的性质

导数

$$ \frac{d}{dt}B_i^{(n)}(t)=n[B_{i-1}^{(n-1)}(t)-B_i^{(n-1)}(t)] $$

$$ \frac{d^2}{dt^2}B_i^{(n)}(t)=n(n-1)[B_{i-2}^{(n-2)}(t)-2B_{i-1}^{(n-2)}(t)+B_i^{(n-2)}(t)] $$

升阶

$$ (1-t)B^n_i(t)=(1-\frac{i}{n+1})B^{(n+1)}_i (t) $$

$$ tB^n_i(t)=\frac{i+1}{n+1}B^{n+1}_i (t) $$

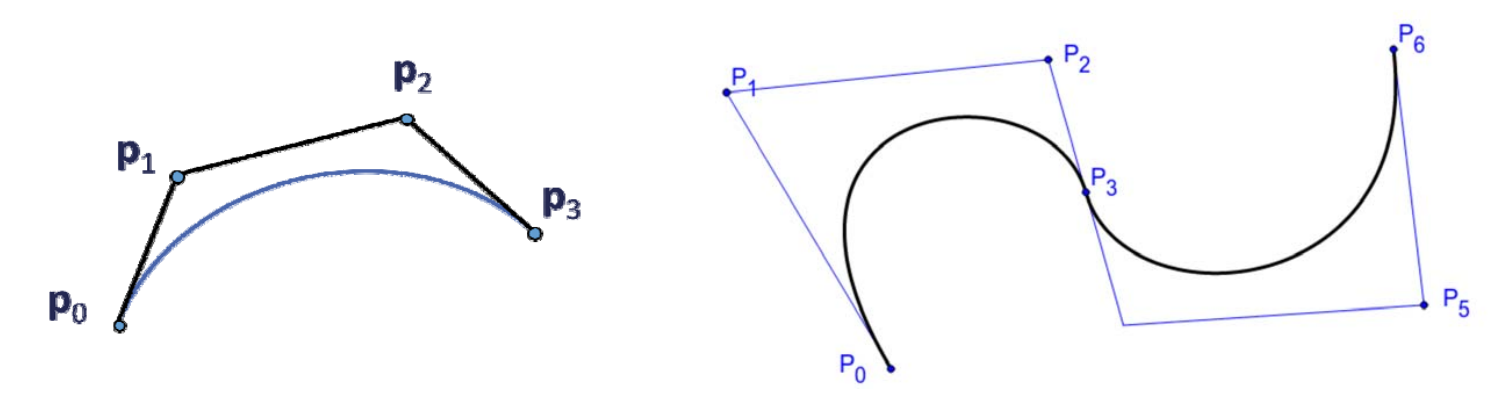
Bezier曲线的性质

凸包性

凸包性：曲线在控制点组成的多边形内部。

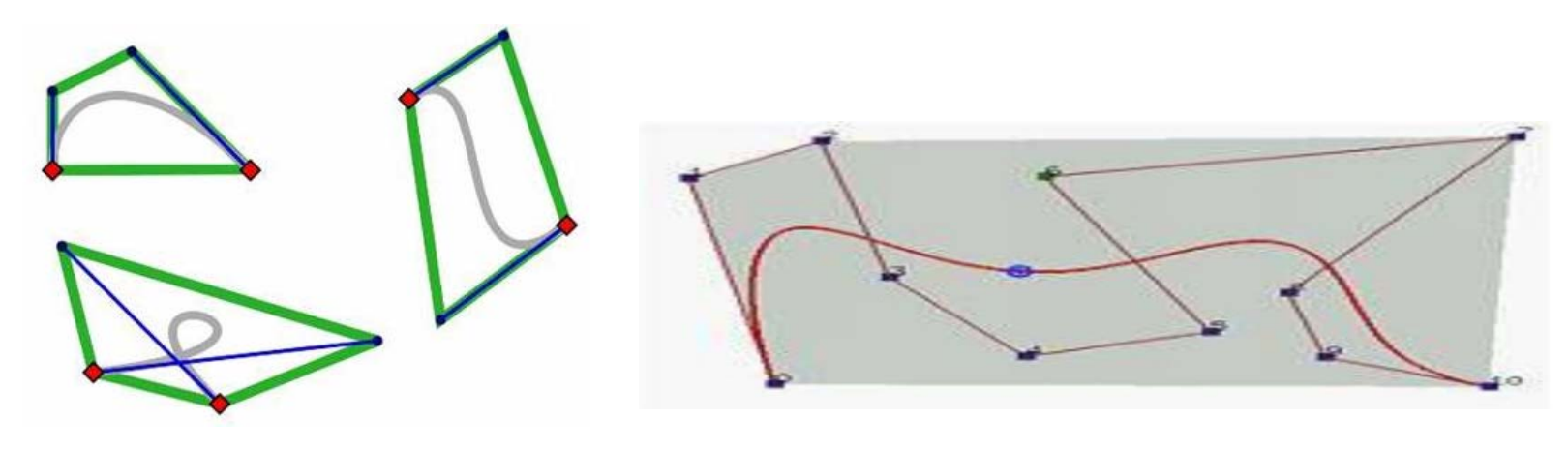
系数满足性和权性的线性组合称为凸组合。

端点插值性

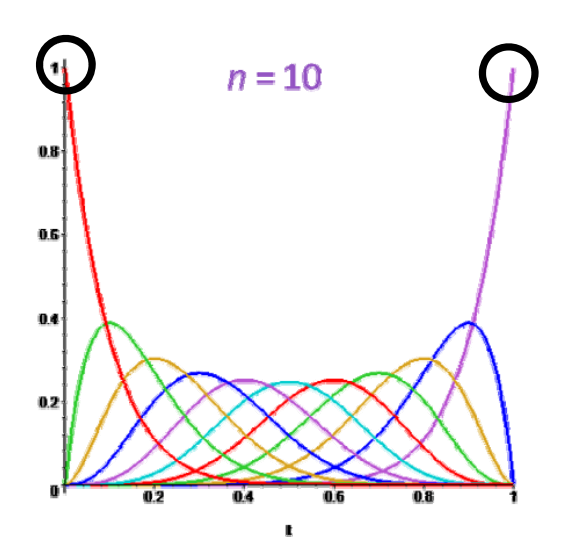
$$ B_0^0(0)=1,B_1^n(0)= \dots B_n^n(0)=0 $$

$$ B_0^n(1)= \dots =B_{n-1}^n(1)=0,B_n^n(0)=1 $$

$$ \downarrow $$

Bezier曲线经过首末两个控制顶点\(p_0,p_n\)

导数

Bezier曲线的导数（切线）
已知\(p_0,\dots ,p_n,f(t)=\sum_{i=0}^{n} B_i^n(t)p_i\)，可得：

$$ {f}' (t)=n\sum_{i=0}^{n-1} B_i^{n-1}(t)(p_{i+1}-p_i) $$

$$ f^{[r]} (t)=\frac{n!}{(n-r)!} \cdot \sum_{i=0}^{n-r}B_i^{n-r}(t)\cdot \Delta ^r p_i $$

Bezier曲线的端点性质

端点插值：
$$ f(0)=p_0 $$

$$ f(1)=p_n $$

端点的切线方向与边相同：

$$ (f)'(0)=n[p_1-p_0] $$

$$ (f)'(1)=n[p_{n-1}-p_n] $$

端点的2阶(k)切线与3点(k+1)相关：

$$ (f)''(0)=n(n-1)[p_2-2p_1+p_0] $$

$$ (f)''(1)=n(n-1)[p_n-2p_{n-1}+p_{n-2}] $$

结合几何意义来理解

升阶

根据Bernstein基的升阶公式可得出Bezier曲线的升阶性质：

$$ f(t)=\sum_{i=0}^{n+1} B_i^{n+1}(t)[\frac{n+1-i}{n+1} p_i+\frac{i}{n+1} p_{i-1}] $$

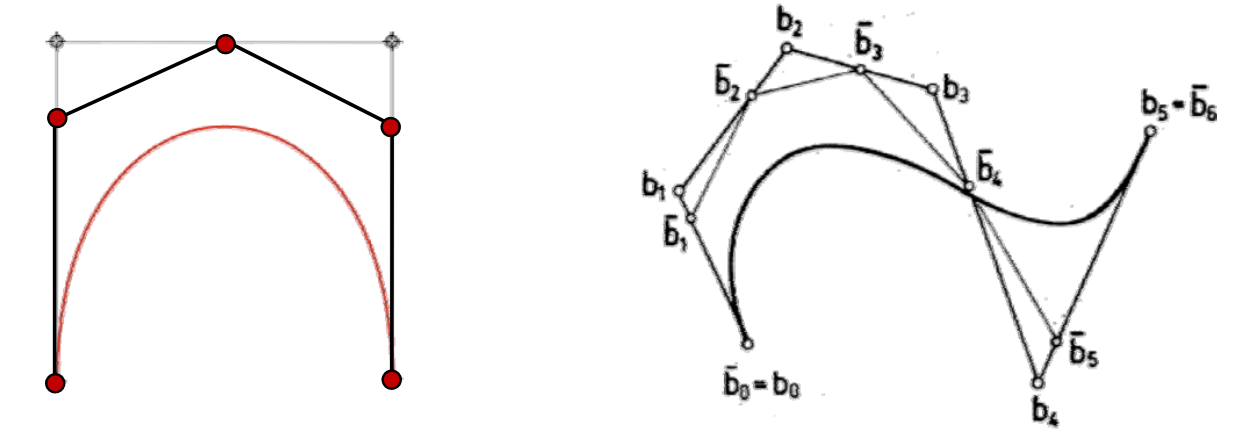
系数为4个控制点，黑色为5个控制点，但它们生成的曲线相同。 所生成的桔色曲线本质阶数是3阶。

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/