隐式曲线的绘制

输入：一个二元隐式函数\(z=f(x,y)\)
输出：值为\(0(或a)\)的等值线\(z=0\)（或\(z-a=0\)）

目的：
• 将隐式曲线转化为参数形式、离散曲线（多边形）形式
• 绘制曲线

Marching Cubes算法 [Siggraph1987]

隐式曲线绘制的最常用方法，网上能找到很多开源实现代码

思想（2D: Marching Squares）

• 在一些离散格子点上求值
• 然后利用局部连续性插值出值为0的点
• 按一定的顺序连接这些点形成离散曲线

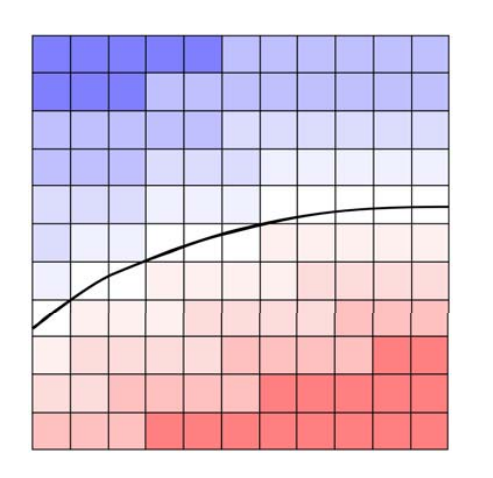
当格子点足够密，曲线性质基本上符合格子性质。

歧义情况

In some cases, different topologies are possible which are all locally plausible:

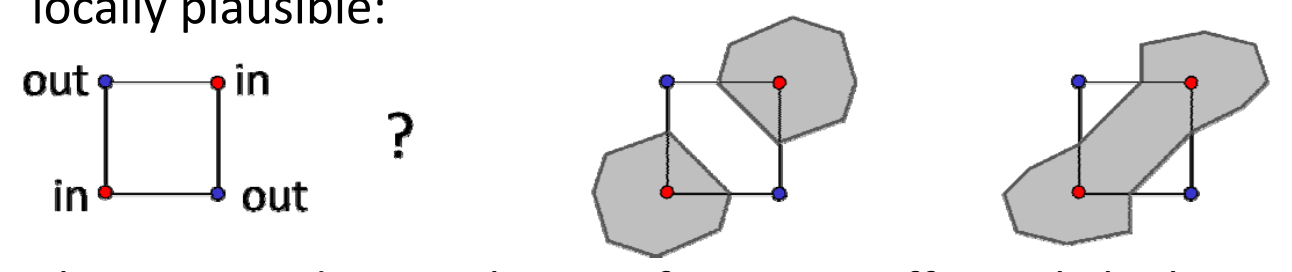
解决方法：
1.This is an undersampling artifact，可通过提高分辨率（加密）解决
2.判断函数导数

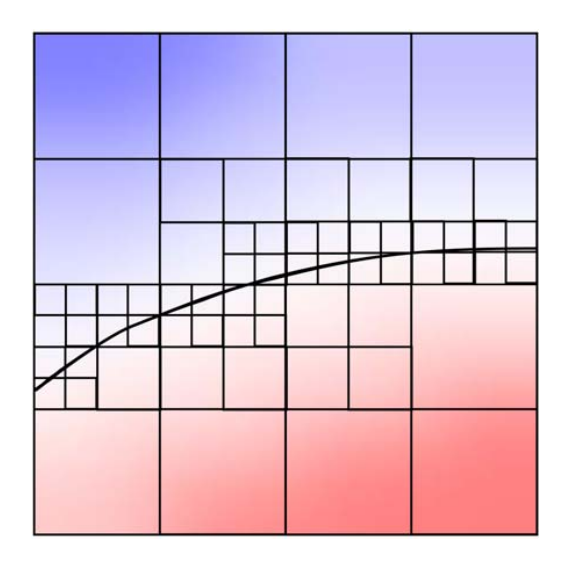
Adaptive / hierarchical grids

Perform a quadtree / octree tessellation of the domain (or any other partition into elements)
Refine where more precision is necessary (near surface, maybe curvature dependent)
Associate basis functions with each cell (constant or higher order)

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/