三次基样条

这一节没讲，用Hermit基组成样条叫基样条。

$$ S(x)=\sum_{i=0}^{n}y_i \varphi _i(x)+{y}'_0 \varphi _{n+1}(x)+{y}'_n \varphi _{n+2}(x) $$

其中\(\varphi _i(x)\)均为三次样条函数，且满足

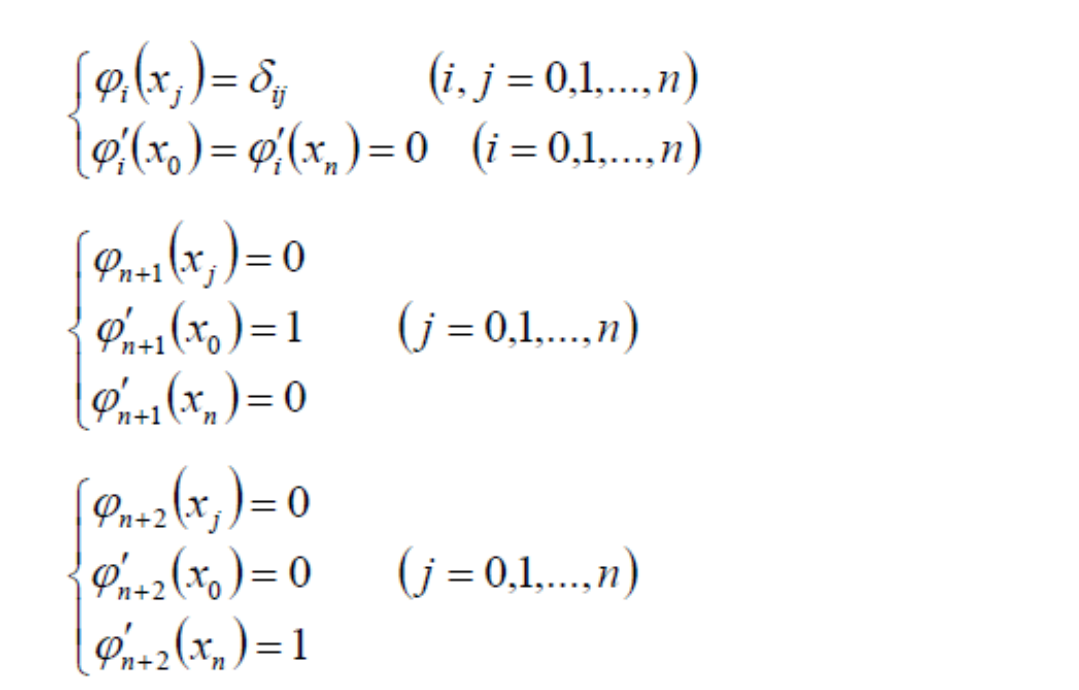
任一\(\varphi _i(x)\)可由三次样条函数方法求得。

[29:35] # ？不知道在干什么.大概是用 Hermit 类似的方法简化求三次基样条的过程。
[>]这个简化方法有点像拉格朗日优化。

基样条特征

• 考虑定义在所有整数节点上的基样条
即满足\(\varphi (j)=\delta _{0j}\),\((j=0,\pm1,\pm2,...)\)

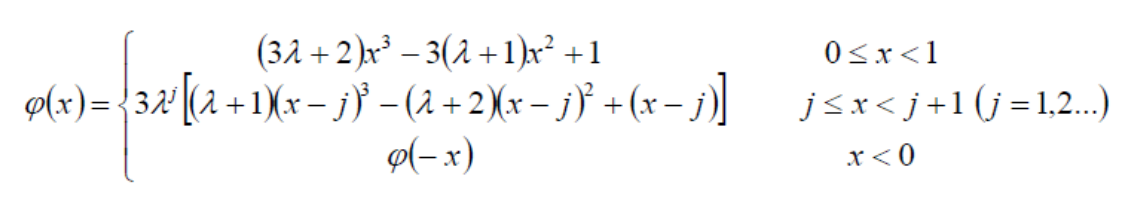
$$ \lambda =\sqrt{3} -2\approx - 0.268 $$

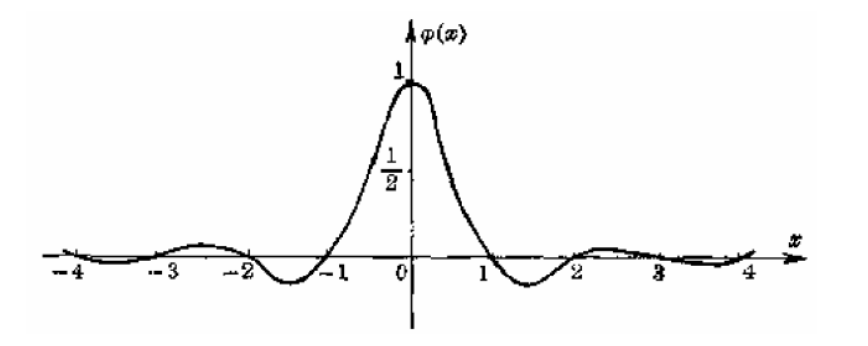
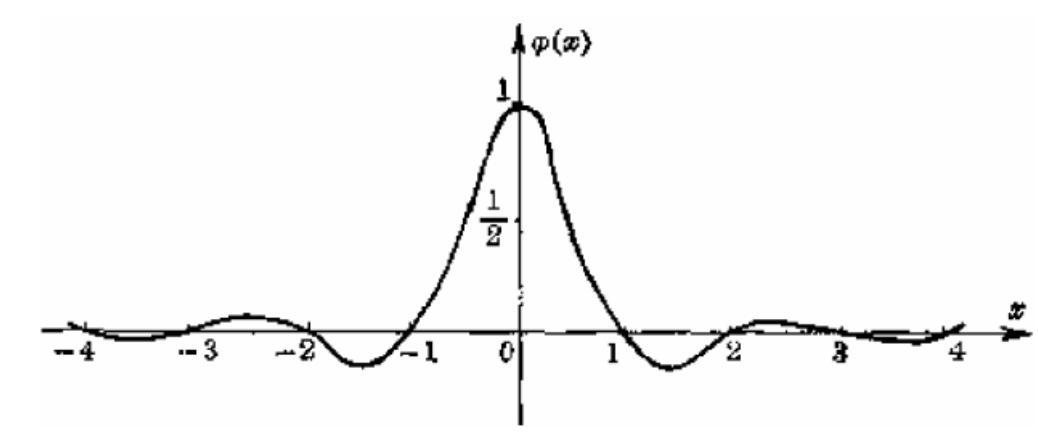
(a) 相邻两端异号；
(b) 每段有一个极值点，\(j+1\)段极值点是j段极值点的\(\lambda\)倍;
(c) 节点处导数满足\(m_{j+1}=\lambda m_j\)

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/