三次样条函数的来源

[14:00]

👆 每个三角形代表一个压铁。

物理推理过程省略，最后结论是两压铁间\(y(x)\)为三次函数，即样条曲线为分段三次函数。

❓ 问：为什么是3次？
答：2次多项式无法表达拐点，不够自由。高次（4次及以上）多项式拐点多，次数若较高计算易出现较大误差。3次正好

三次样条曲线的求解

已知每个压铁的位置，求压铁之间的三次函数。思考：
• 每段多项式函数之间满足什么条件？
• 如何求解？

求解思路

根据已知条件来定义变量

每段为3次多项式，因此每一段函数的形式如下，且有4个变量（待定系数）

$$ y_i(x)=a_i+b_ix+c_ix^2+d_ix^3 $$

假设有\(n+1\)个型值点（\(n\)段），则总共有个\(4n\)变量。

根据已知条件来设置约束

• 首先，曲线要插值型值点，有\(n+1\)个约束条件；
• 其次，假设曲线整体为\(C^2\)连续，则相邻两段在拼接点要满足3个条件（\(C^0\)连续、\(C^1\)连续、\(C^2\)连续）；则有\(3n-3\)个约束条件；

到目前为止共有\(4n-2\)个约束条件；因此，再加2个额外条件，即可唯一确定整条曲线。

根据边界条件来设置约束

在首尾的控制点上各增加一条约束，见[23:36]的边界条件。例如：

• 自由端：指定曲线在两个端点处的二阶导数值
  特别地，两个端点的二阶导数值指定为0时称为自然三次样条

• 夹持端： 指定曲线在两个端点处的一阶导数值

• 抛物端：首末两段为抛物线

• 周期端

• 混合边界条件

方法1

1. 引入中间变量：节点处的2阶导数值\(M_i\)（弯矩）
2. 每段\({y}''(x)\)表达为\(M_i\)和\(M_{i+1}\)的线性插值，则\(y_i(x)\)为包含待定值\(M_i\)的3次多项式
3. 再根据拼接条件（\(C^0\)、\(C^1\)、\(C^2\)连续），列出等式
4. 最后加上2个边界条件，构成关于{\((M_i,i=1,...,n-1)\)}的\((n-1)\times (n-1)\)阶的线性方程组
   方程组为对称的、三对角的、对角占优的，称为三弯矩方程组。方程组系数矩阵满秩，有唯一解。可用追赶法求解三弯矩方程组。

方法2

1. 引入中间变量：节点处的1阶导数值\(M_i\)（转角）
2. …（推导过程类似）
3. 最后加上2个边界条件，构成关于{\(M_i,i=1,...,n-1\)}的\((n-1)\times(n-1)\)阶的线性方程组
   方程组为对称的、三对角的、对角占优的，称为三转角方程组。方程组系数矩阵满秩，有唯一解。同样可用追赶法求解三转角方程组。

简化的计算技巧

Hermite型插值多项式

如果已知两个压点的位置及一阶导，则可以快速求出三次曲线(Hermite)。

假设

$$ \begin{cases} S(x_{i-1})=f_{i-1}\\ S(x_i)=y_i \end{cases} $$

$$ \begin{cases} {s}' (x_{i-1})=m_{i-1} \\ {s}' (x_i)=m_i \end{cases} $$

预先求出一组满足性质的四条曲线，分别是（1）经过x0且其它点都为0（2）经过x1且其它点都为0（3）x0的导数满足要求，其它都为0（4）x1的导数满足要求，其它都为0
其它曲线都可以通过这四条曲线组合出来。

当\(x=\in [x_{i-1},x_i]\)时，有
$$ S(x)=y_{i-1}h_0(x)+y_ih_1(x)+m_{i-1}H_0(x)+m_iH_1(x) $$

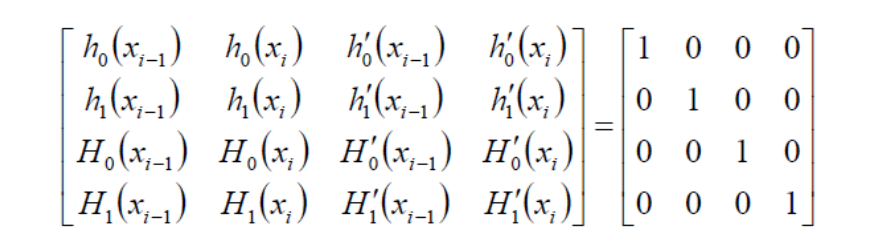
对函数有4个约束：
分别针对每个约束得到4个函数，即 \(h_0,h_c,H_0,H_1\)。
\(s(x)\)为这4个函数的线性组合。

Lidstone型插值多项式

已知两个压点的位置和二阶导，也能快速求出曲线。

具体过程没讲，跟上面的方法类似

好处：在给定两个端点及其导数情况下，可直接写出函数的表达形式，这是数学上的一个通用技巧

❓ 虽然没怎么听懂，但感觉是类似【技巧1构造插值问题的通用解】(link)的一种方法。

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/