隐函数定理

对于任意的隐函数，全局上很难写出 \(y=f(x)\)形式。
但在任意一个局部，可以定义出\(y=f(x)\)

隐式曲线的绘制

将隐函数升高一维，看成是\(x\)和\(y\)的二元函数
\(z=f(x,y), \)
\(x,y\in [a,b]\times [c,d]\)

则该隐式曲线为上述二元函数的0等值线（平面\(z=0\)与\(z=f(x,y)\)的交线）

• \(f(x,y)=0\), 曲线上；
• \(f(x,y)<0\), 曲线的左侧（内部）；
• \(f(x,y)>0\), 曲线的右侧（外部）；

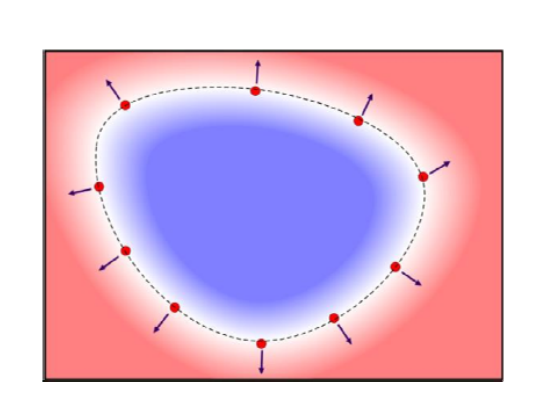
找一个隐式函数上的点的过程称为显式化或参数化。这是一个比较难的问题，常用方法是Marching Cube。

隐式函数表达

已知一条封闭曲线，如何构造隐式函数表达？

General case

• Non‐zero gradient at zero crossings
• Otherwise arbitrary

没有解释这种方法

Signed implicit function:

sign (𝑓):

• 负：inside
• 正：outside

Signed distance field (SDF)

|𝑓|：distance to the surface
sign(𝑓): negative inside, positive outside

Squared distance function

𝑓 = \((\)distance to the surface\()^2\)

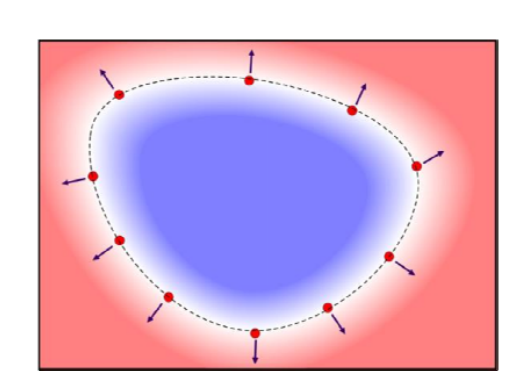
微分属性 Differential Properties

对于曲面表面上的点x，满足以下性质：

• \( 𝑓(𝒙)=0\)

• 假设\(𝛻𝑓(𝒙)\ne 0\)，否则为奇异点，不考虑这种情况

• unit normal为：
  $$ 𝑛(𝒙)=\frac{\nabla f(x) }{||\nabla f(x)|| } $$

  • For signed functions, the normal is pointing outward
  • For signed distance functions, this simplifies to 𝒏(𝒙)=𝛻𝑓(𝒙)

• mean curvature与the divergence of the unit normal成正比:
  $$ -2𝐻(𝒙)=𝛻⋅𝒏(𝒙)=\frac{𝜕}{𝜕𝑥} n_x(x)+\frac{𝜕}{𝜕y}ny(x)+\frac{𝜕}{𝜕z}n_z(x)\\ =𝛻 ⋅\frac{𝛻𝑓(𝒙)}{||𝛻𝑓(𝒙)||} $$

  • For a signed distance function, the formula simplifies to:

$$ -2𝐻(𝒙)=𝛻 ⋅ 𝛻𝑓(𝑥)=\frac{𝜕^2}{𝜕𝑥^2} f(x)+\frac{𝜕^2}{𝜕y^2}f(x)+\frac{𝜕^2}{𝜕z^2}f(x)=𝛻𝑓(𝑥) $$

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/