优化问题的一般形式
优化问题的目标函数一般是实值函数,因为实数才能比大小
不同的\(g(x) 和 h(x)\),用不同的方法优化。
高维实值函数:\(f:\mathbb{R}^n\to \mathbb{R}\)
| \(\min_x\in \mathbb{R} ^nf(x)\) | 目标函数 or 能量函数 |
| S.t.\(g(x)=0\) | 等式约束 |
| \(h(x)\ge 0 \) | 不等式约束 |
不同的优化问题须用不同的优化方法
特定的优化问题需要设计特定的优化方法达到最佳性能
概念
梯度 (Gradient):一阶导数
$$ f:\mathbb{R}^n\to \mathbb{R} $$
$$ f=(\frac{\partial f}{\partial x_1} ,\frac{\partial f}{\partial x_2} ,\cdots ,\frac{\partial f}{\partial x_n}) $$
Jacobian: 一阶“导数”矩阵
$$ f:\mathbb{R}^n\to \mathbb{R}^m $$
$$ (D_f)_{ij}=\frac{\partial f_i}{\partial x_j} $$
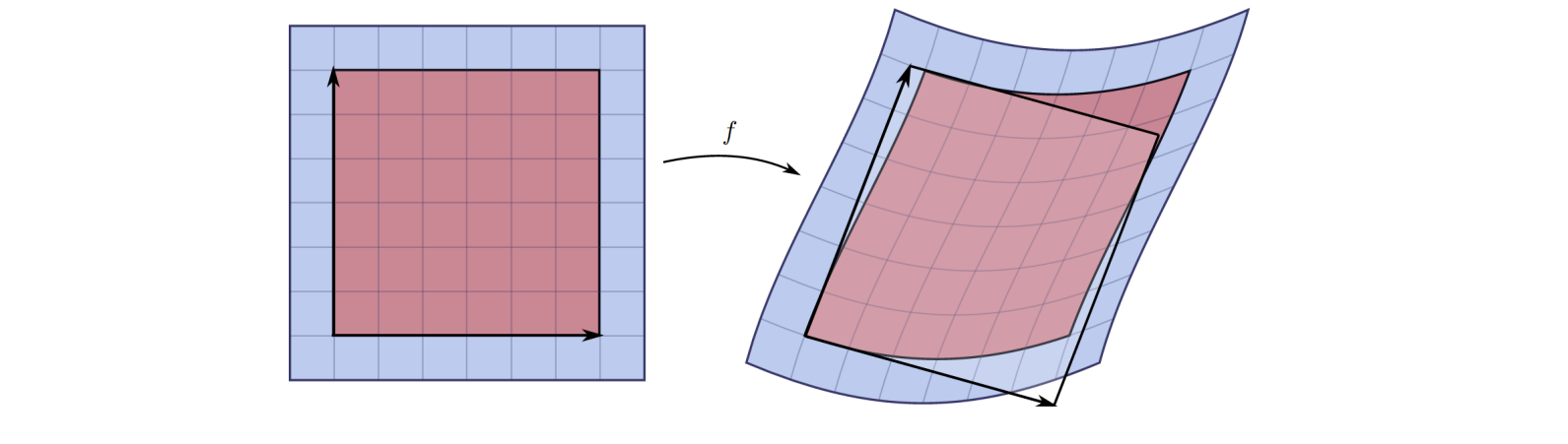
Hessian :二阶“导数”矩阵
$$ f:\mathbb{R}^n\to \mathbb{R} \to H_{ij}=\frac{\partial^2 f}{\partial x_i\partial x_j} $$

$$ f(x)\approx f(x_0)+\nabla f(x_0)^\top (x-x_0)+(x-x_0)^\top Hf(x_0)(x-x_0) $$
[57:31] 每个分量对每个变量求导构成的矩阵
H是函数的二阶项的度量
驻点(Critical point)
$$ \nabla f(x)=0 $$
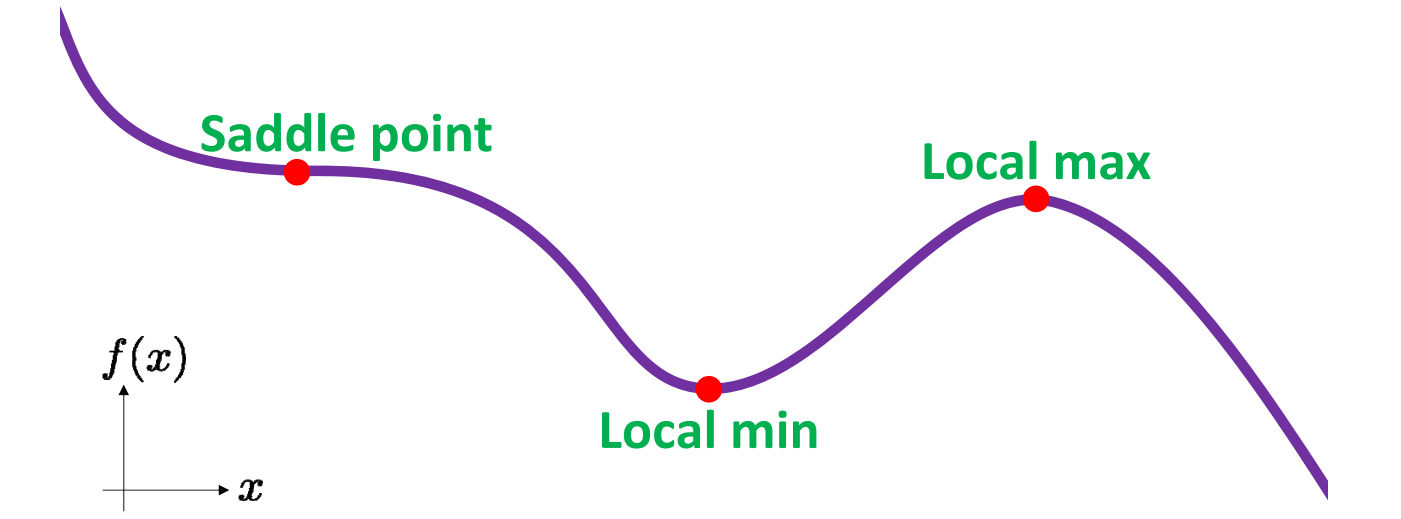
Critical points may not be minima.
一般非线性函数的最小值
无法直接求解,可以从某初值开始,逐步找其附近的极小值
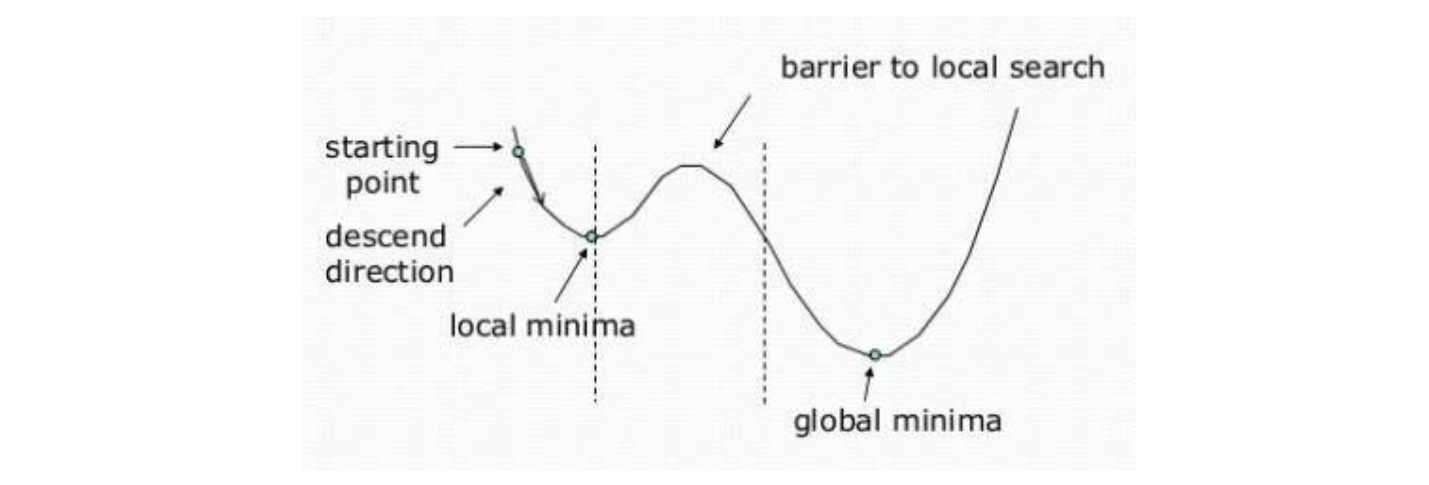
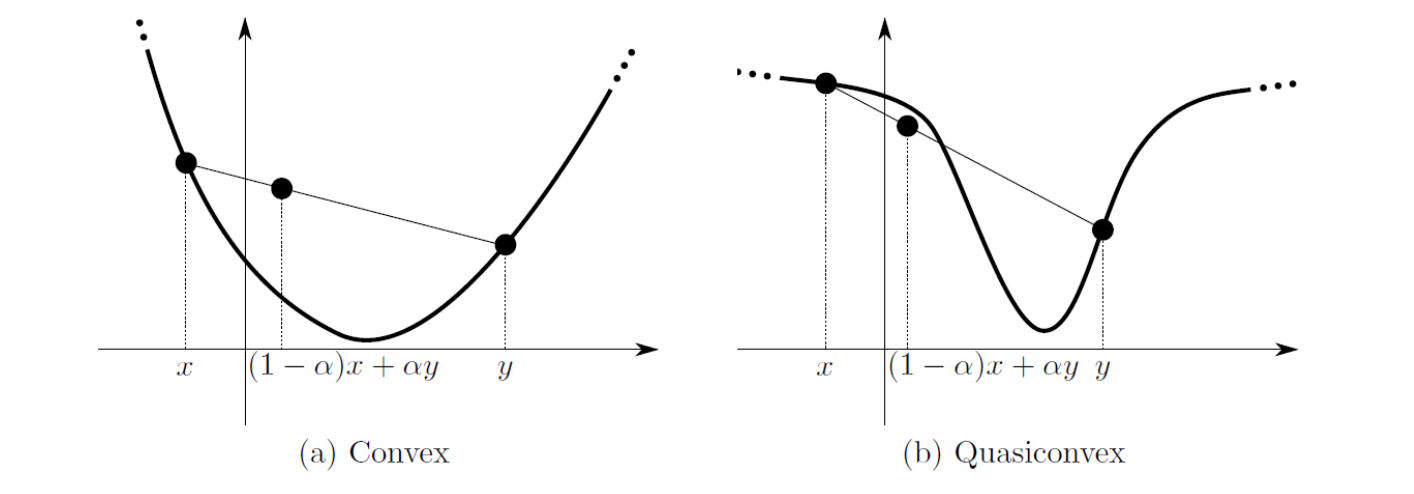
凸函数的驻点就是最小值
优化问题的类型
• Constrained / Unconstrained
• Linear / Nonlinear
• Global / Local
• Convex / Nonconvex
• Continuous / Discrete
[1:03:25] Discrete:只在整数域上找最优解。
• Stochastic / Deterministic
• Single objective / Multiple objectives
多目标常常是矛盾的,需要做权衡,找平衡点或通过权重结合成单目标问题。
minimize \((E_1(x),E_2(x),\cdots ,E_k(x))\)
\(E=\lambda _1E_1+\lambda _2E_2+\cdots +\lambda _kE_k\)
本文出自CaterpillarStudyGroup,转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/