Chaikin割角法[1974]

具体步骤

加在哪：每条边取中点，生成新点

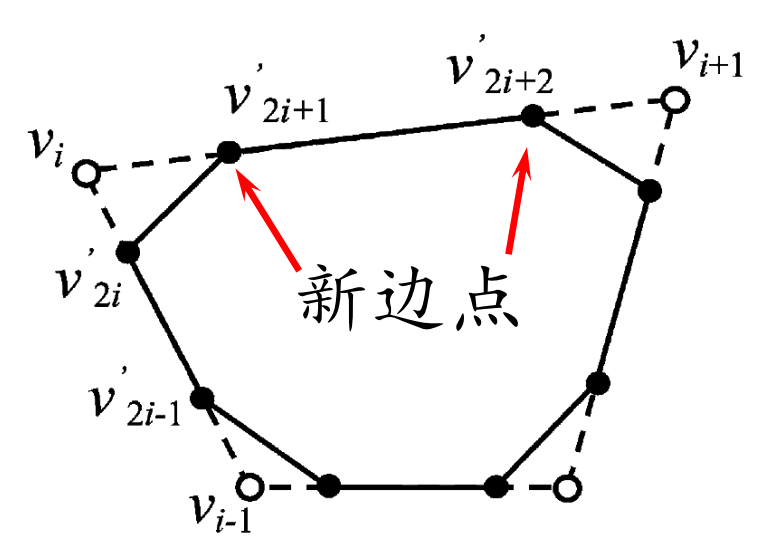
在哪加：每个点与其相邻点平均（顺时针），点分裂成边（割角），老点被抛弃（逼近型）

$${\nu }' _{2i}=\frac{1}{4} \nu _{i-1}+\frac{3}{4} \nu _i$$

$${\nu }' _{2i+1}=\frac{3}{4} \nu _{i}+\frac{1}{4} \nu _{i+1}$$

迭代生成曲线

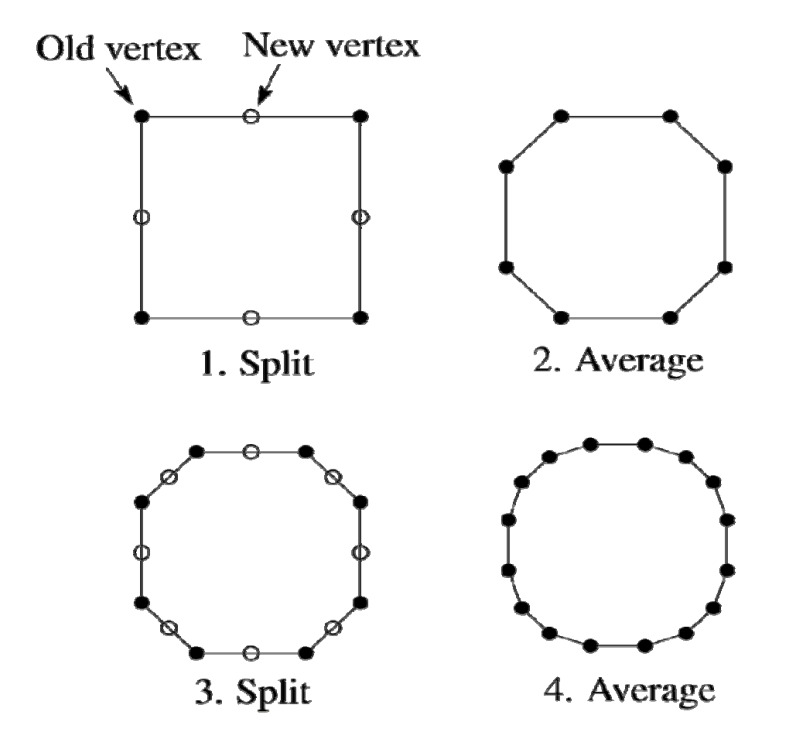
细分结果

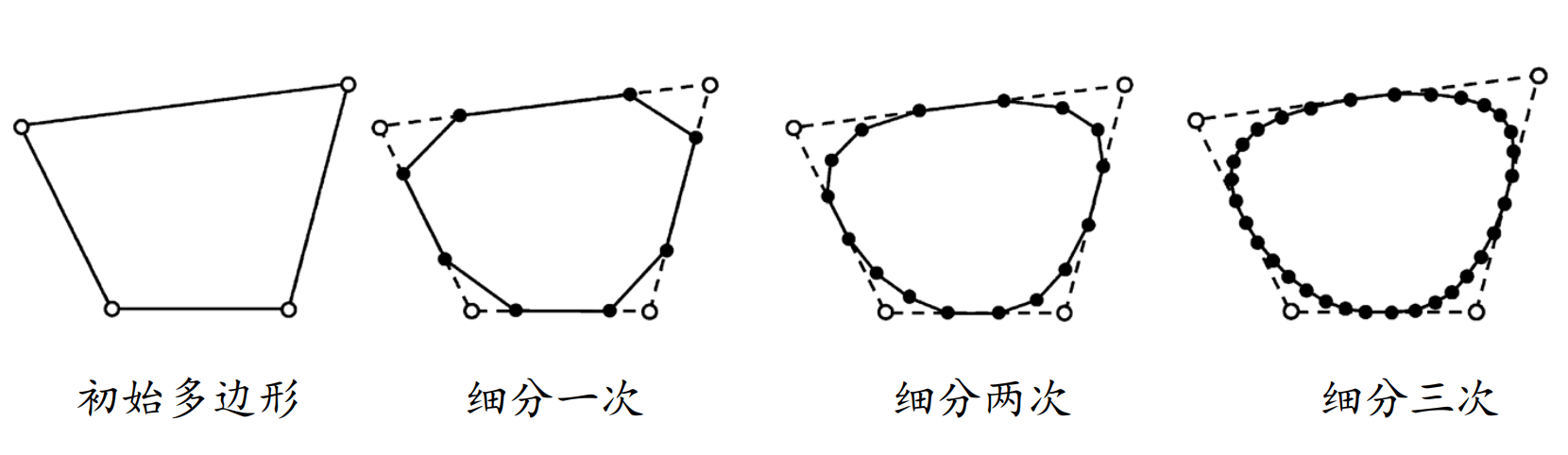
收敛后的极限曲线是由初始多边形决定的二次均匀B样条曲线。
节点处$𝐶^1$，其余点处$𝐶^\infty$

均匀三次B样条曲线细分方法

• 拓扑规则：边分裂成两条新边
• 几何规则：

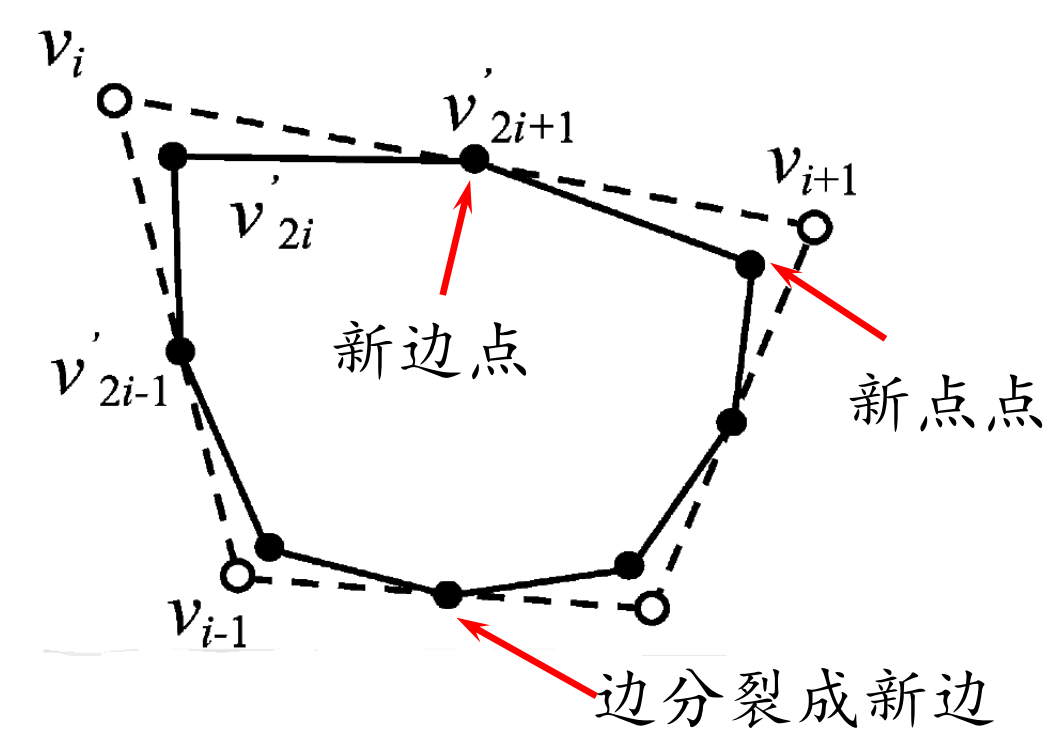
$${\nu }' _{2i}=\frac{1}{8} \nu _{i-1}+\frac{3}{4} \nu _i+\frac{1}{8} \nu _{i+1}$$

$${\nu }' _{2i+1}=\frac{1}{2} \nu _{i}+\frac{1}{2} \nu _{i+1}$$

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/