从数学开始

数学是一种语言。用数学语言进行建模的过程：问题→模型->算法->代码。使用数学语言要擅长抽象。

👆 科学研究的过程

✅ 其中，对问题建模的能力是最重要的

集合内容跳过。
线性空间内容跳过。
映射内容跳过。
函数内容跳过。

函数的集合（函数空间）

用若干简单函数（“基函数”）线性组合张成一个函数空间

$$ -L=span\left (f_1,f_2,\dots ,f_n \right ) =({\textstyle \sum_{i=1}^{n}} a_if_i(x)|a_i\in R) $$

每个函数就表达（对应）为\(n\)个实数，即系数向量\((a_1,a_2,\dots ,a_n)\)

例如： 幂基

$$ ( x^{k},k=0,1,\dots ,n ) $$

构成的函数空间

$$ f(x)=\sum_{k=0}^{n} w_{k} x^{k} $$

称为多项式函数空间。

三角函数基构成的函数空间

$$ f(x)=a_{0}+\sum_{k=1}^{n}\left(a_{k} \cos k x+b_{k} \sin k x\right) $$

称为三角函数空间

空间的完备性：这个函数空间是否可以表示（逼近）任意函数？

❗ 函数空间几乎是后面课程整个连续几何部分的基础，理解函数空间对理解后面的课程非常重要。

万能逼近定理

Weierstrass逼近定理：
• 定理1：闭区间上的连续函数可用多项式级数一致逼近
• 定理2：闭区间上周期为\(2π\)的连续函数可用三角函数级数一致逼近
对 \( [a, b] \)上的任意连续函数\(g\), 及任意给定的\(\varepsilon>0 \), 必存在\(n\) 次代数多项式\(f(x)=\sum_{k=0}^{n} w_{k} x^{k} \), 使得 $$ \min _{x \in[a, b]}|f(x)-g(x)|<\varepsilon. $$

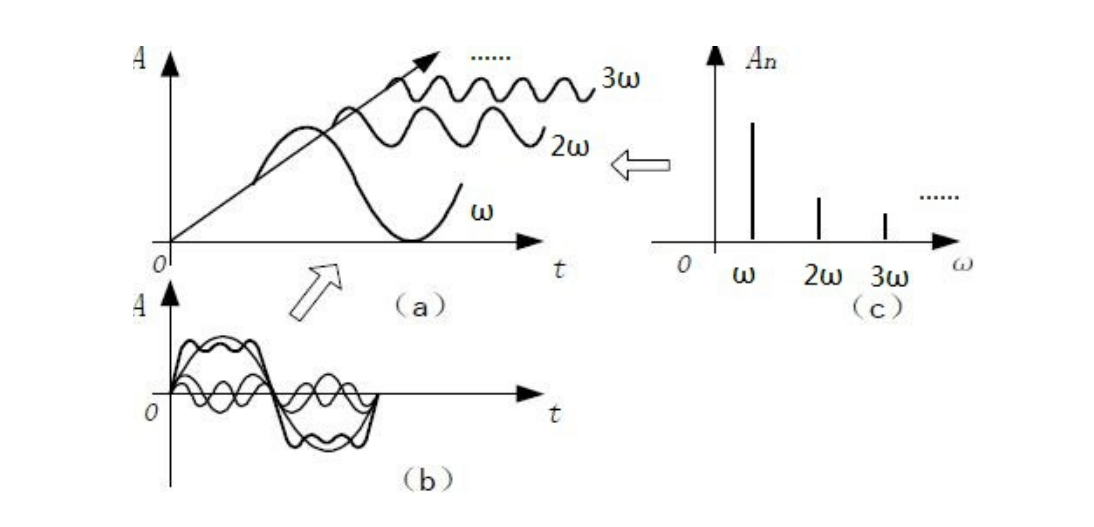
傅里叶级数

$$ f(t)=A_{0}+\sum_{n=1}^{\infty}\left[a_{n} \cos (n \omega t)+b_{n} \sin (n \omega t)\right] $$

$$ f(t)=A_{0}+\sum_{n=1}^{\infty} A_{n} \sin n \omega t+\psi_{n} $$

[47:46] 两个\(f(t)\)是等价的。\(n\)代表对sin的缩放，\(\phi_t\) 代表对 sin 的平移，用一个函数sin通过对它的伸缩和左右平移，就能表达一个任意复杂的周期函数。

更复杂的函数：函数复合

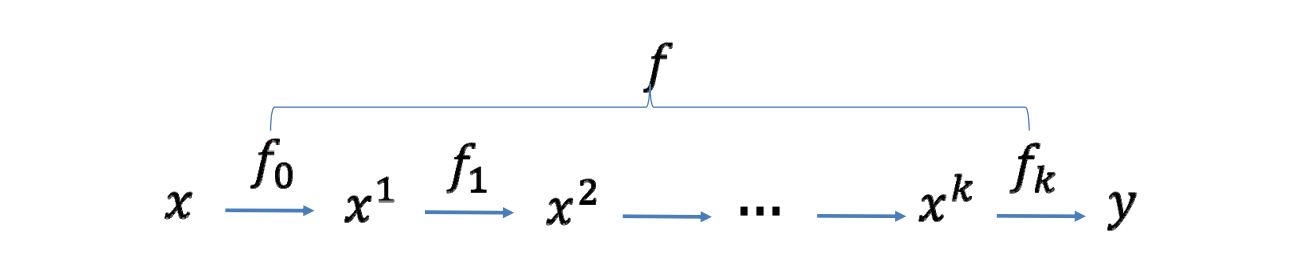
$$ f=f_{k}{ }^{\circ} f_{k-1}{ }^{\circ} \ldots{ }^{\circ} f_{0} $$

问题：如何求满足要求的函数？

🔎 [51：11]

大部分的实际应用问题

• 还需要根据实际问题设计输入输出
• 可建模为：找一个映射/变换/函数
• 输入不一样、变量不一样、维数不一样

如何找函数的三步曲：

• 到哪找，即确定某个函数集合/空间
  ①各种网络模型(CNN，RNN)都是在解决“到哪找”的问题
• 找哪个，即度量哪个函数是好的/“最好”的
  ②各种Loss定义(L2,交叉熵)都是在解决“找哪个”的问题
• 怎么找，即求解或优化。可以选择不同的优化方法与技巧，目标是既要快、又要好…
  ③各种优化方法(牛顿下降、Adam)都是在解决“怎么找”的问题

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/