Local Laplacian Smoothing 方法存在的问题
- 不同位置收敛速度不同
- 自交
Global Laplacian Smoothing
极小曲面
方法
极小曲面(minimal surface) = 平均曲率处处为0 = 微分坐标一致为0
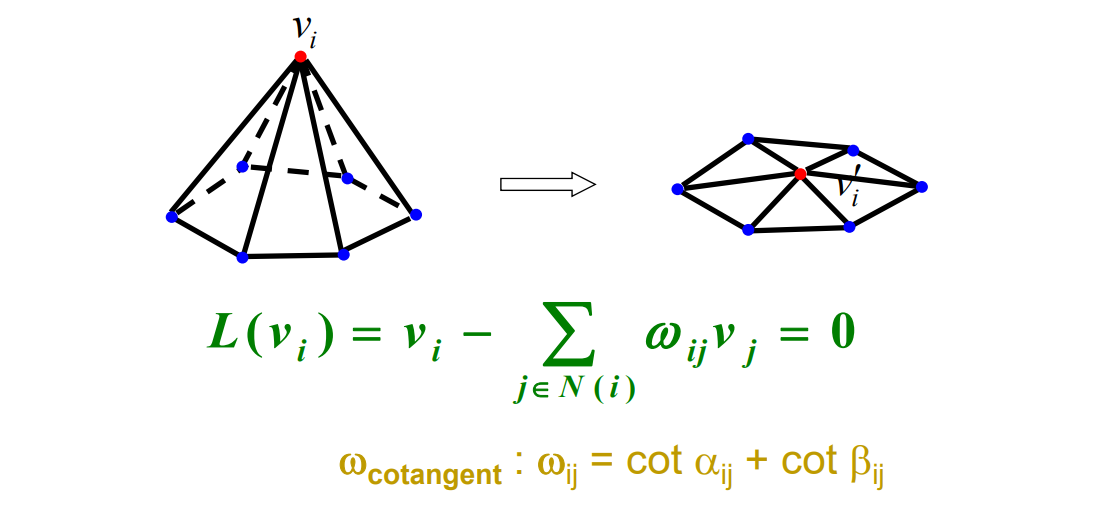
所有顶点的方程联立,得到网格曲面的整体Laplacian方程:
$$ Ax = 0 \\ x=(v_1,v_2,\dots ,v_n)^\top $$ \(A 的第 i 行为 (v_i)的系数,即 第i个系数为1,第j个系数为 w_{ij}\),其余为0.整体上非常稀疏。
应用:生成极小曲面
- 检测边界,固定边界
- 构建稀疏方程组\((\delta=0)\)
global体现在所有点的约束同时满足,不需要像Local那样迭代出极小曲面。
但是global需要求解方程组,可以用数学方法,也可以用迭代方法。
- 求解稀疏方程组
注:有高效的求解方法,且有成熟的数学库可使用MLK, Eigen
- 更新内部顶点坐标

任意曲面
也不一定目标是极小曲面,可以是指定曲率的曲面,则Laplacian Matrix为:
方法
$$ A_{ij}=\begin{cases} 1 , i\in N(j)\\ 0, otherwise \end{cases} $$
$$ D_{ij}=\begin{cases} d_i, i=j\\ 0, otherwise \end{cases} $$
$$ L=I-D^{-1}A $$
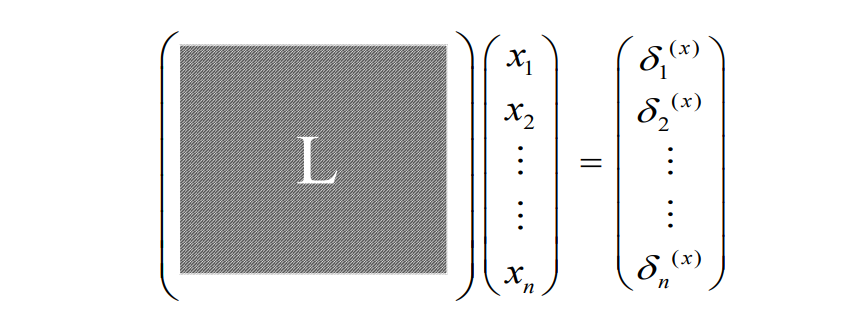
考虑到每个点有x, y, z三个分量,展开来是这样的:
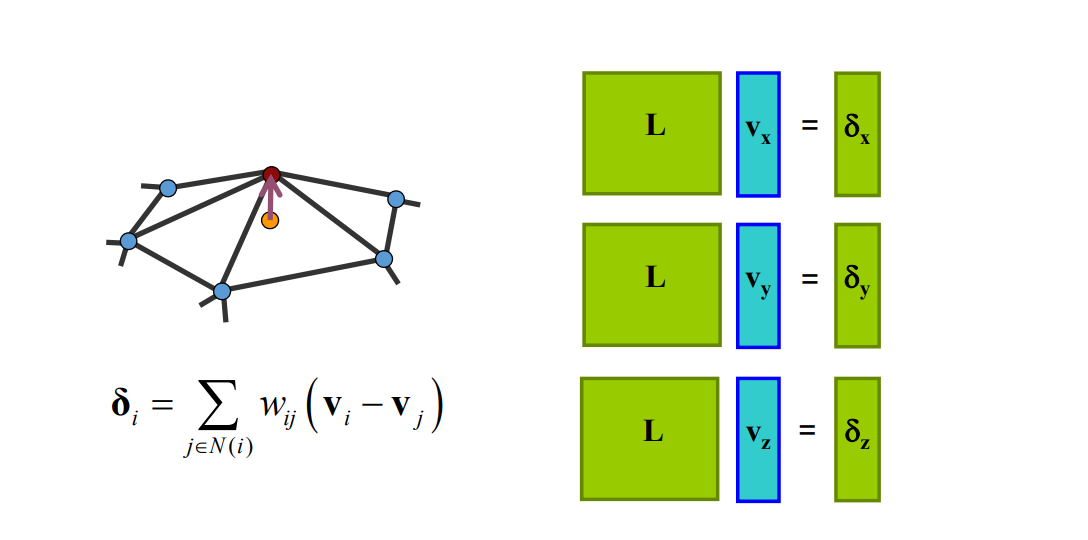
增加将边界点固定的约束。
应用:Reconstruction
根据拓扑关系生成L矩阵,那么在拓扑不变的情况下,就可以根据提前记录下的\(\delta\)还原出原曲面。
$$ Lv=\delta $$
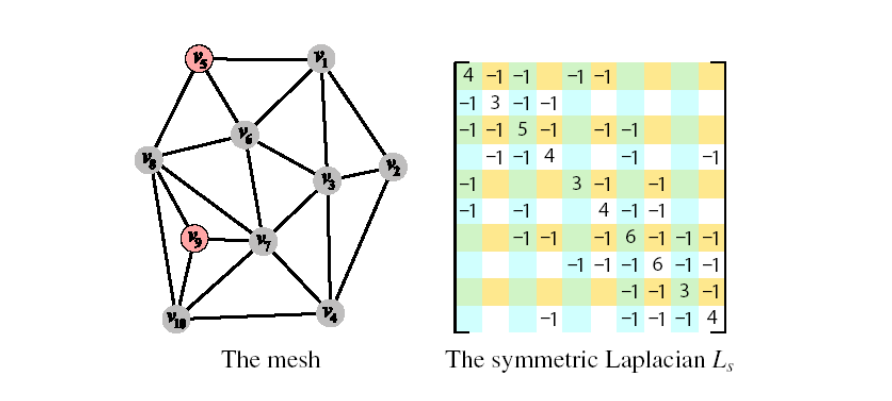
不断减小\(\delta\)而更新V,得到极小曲面。
Rank(L) = n‐c (n‐1 for connected meshes)
L 非满秩, C 为 mesh 的联通个数,至少为1.
必须增加额外约束使L满秩。
本文出自CaterpillarStudyGroup,转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/