Review：3D网格曲面

3D网格曲面是二维流形曲面的离散：link1、link2 、link3

局部特征度量

一个点的信息通常由它周围的顶点和面片来决定。

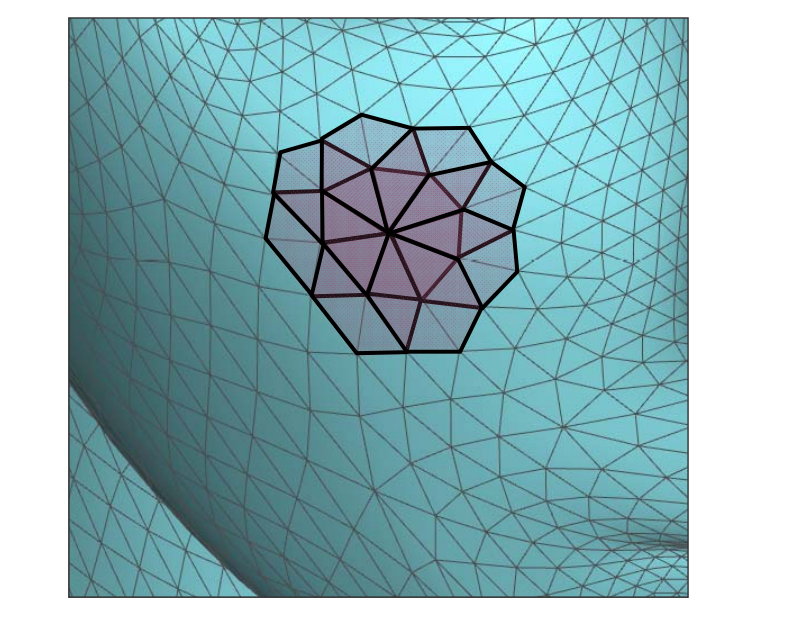
对于离散几何来说，无穷小邻域性质就通过 n 邻域来分近似。

其中最常用的是1‐邻域，即1‐ring neighborhood

离散观点：直接取邻域点的特征来计算当前点的特征
连续观点：取邻域点拟合成曲面，然后分析曲面在该点处的特征。

一般“流形”结构也是通过局部邻域来定义

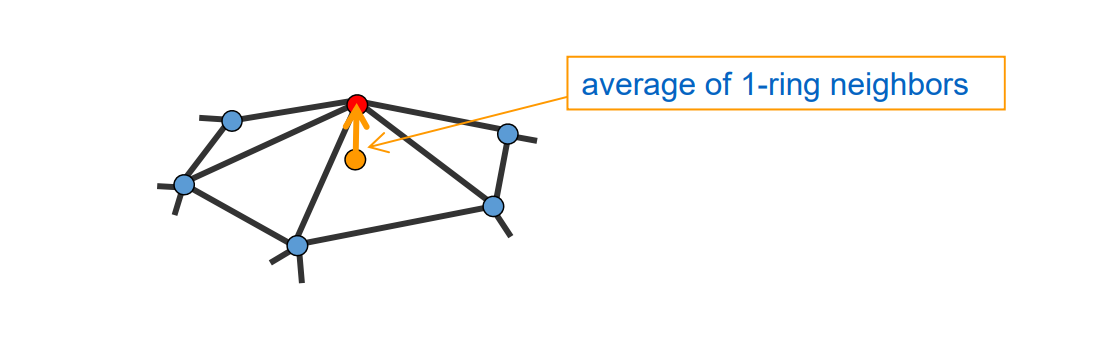
Detail = surface – smooth (surface)
Smoothing = averaging

红点是surface。
黄点是smooth，是蓝点的加权平均，可以用各种加权方式。有哪些权重方法见本页最后。
黄色向量是detail，称为拉普拉斯算子，可以描述红点的尖锐承度。

此页中是连续形式的 Laplace 算子。

$n$维欧几里得空间的二阶微分算子（椭圆型算子）
梯度 $\nabla f$ 的散度 $\nabla \cdot f$

$$ \Delta f=\nabla \cdot \nabla f=\nabla^{2} f $$

梯度是一个向量，散度指向量各个分量之和。

在笛卡尔坐标系中，为所有非混合二阶偏导数：

$$ \Delta f=\sum_{i=1}^{n} \frac{\partial^{2} f}{\partial x_{i}^{2}} $$

特别地，对二元实函数$f(x,y)$：

$$ \Delta f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}} $$

称为Laplace‐Beltrami 算子

$$ \nabla ^2f=\nabla \cdot \nabla f \\ =\frac{1}{\sqrt{|g|} } \partial _i(\surd |g|g^{ij}\partial _jf). $$

又称为Umbrella Operator、伞型算子

$$ \delta _i=\nu _i-\sum _{j\in N(i)}w_j\nu _j $$

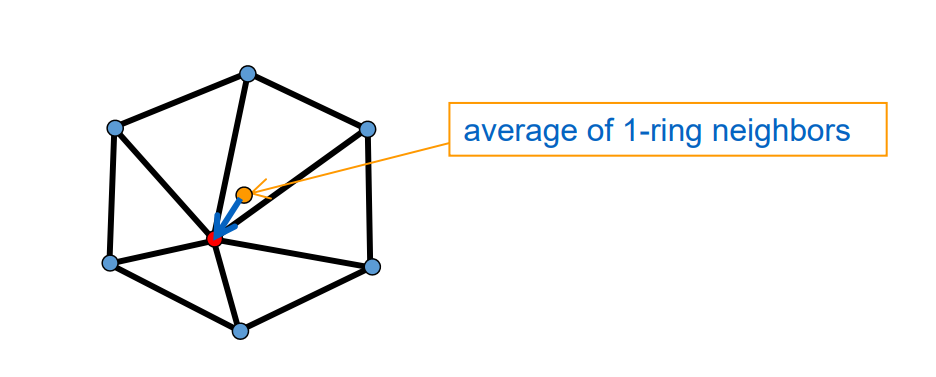
❓ 如何理解离散曲面的Laplace比算子？[23:40]

后向差分：

$$ {f}'_ x=\frac{y_ {i+1}-y_i}{x_ {i+1}-x_ i} $$

前向差分： $$ {f}'_ x= \frac{y_ i-y_ {i-1}}{x_ i-x_ {i-1}} $$

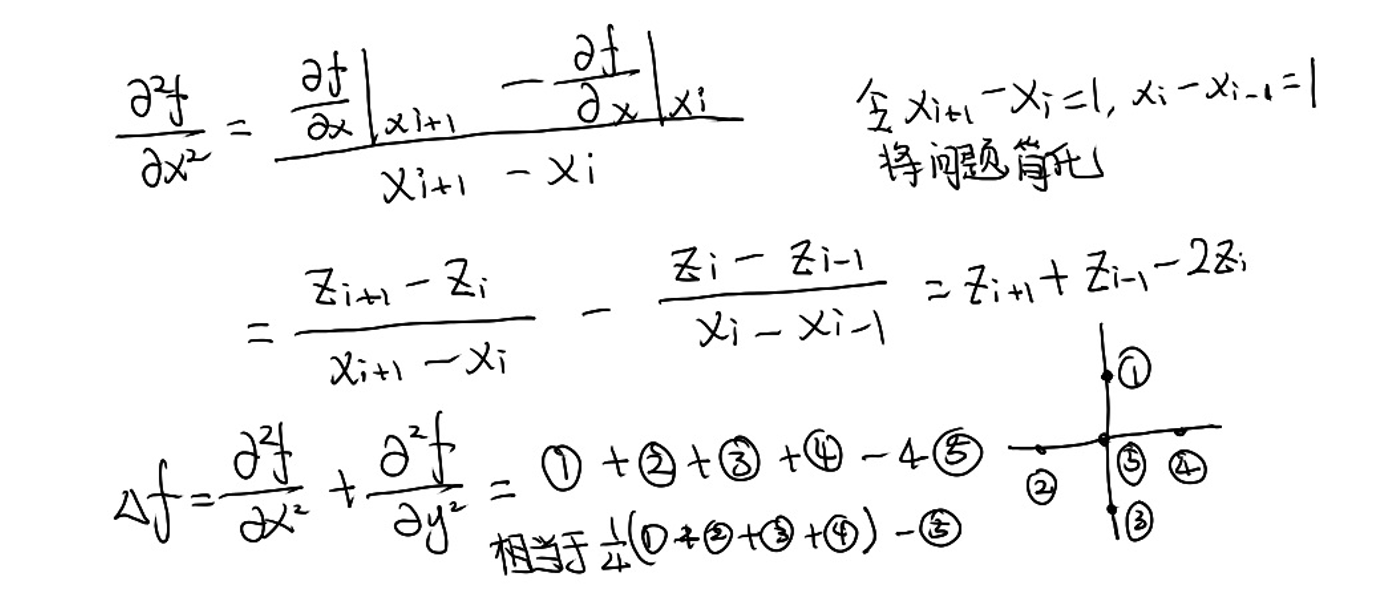
① ② ③ ④ 看作是⑤的 1 邻域。
推广到一般形式可得：$\delta _i$
$\delta _i$称为 Laplace 算子，也叫 Laplace 坐标、微分坐标。

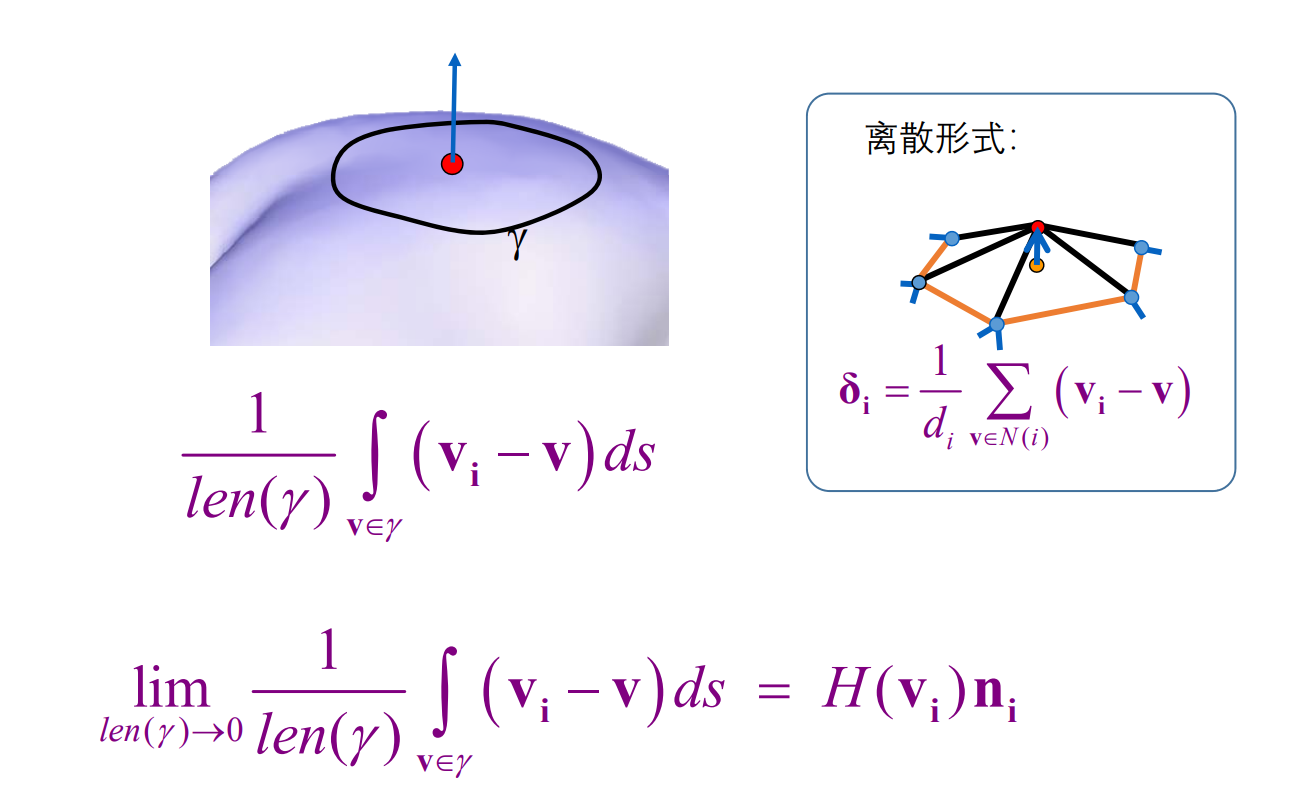
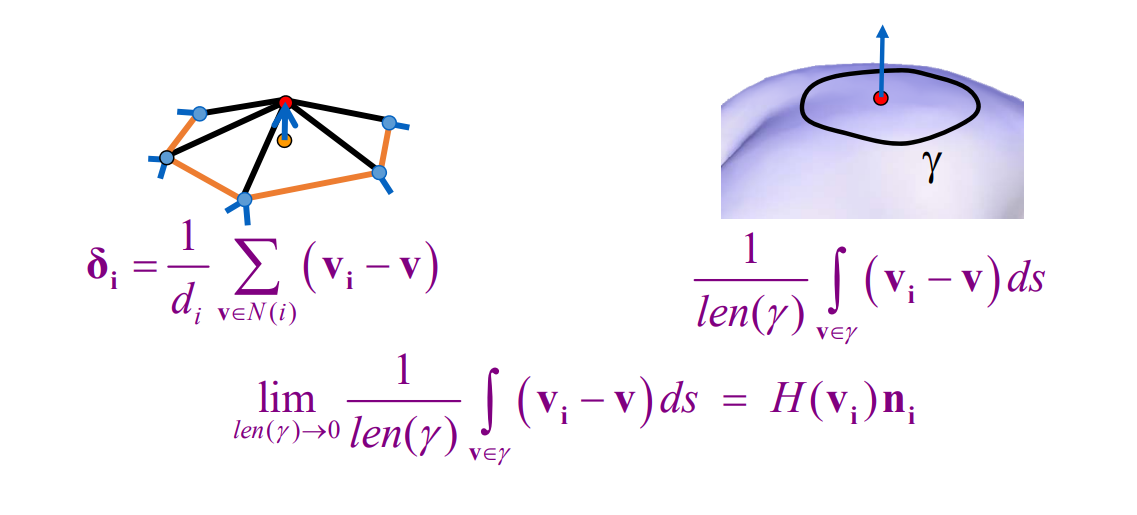
平均曲率流定理：link

将此定理公式写成离散形式，与$\delta _i$公式相通。

微分坐标 represent the local detail / local shape description，具有与$H(v_i)n_i$相同的特点：

• Uniform weight (geometry oblivious)

$$ w_i=1 $$

• Cotangent weight (geometry aware)

$$ w_j=(\cot \alpha +\cot \beta ) $$

• Normalization

$$ w_j=\frac{w_j}{\sum _jw_j} $$

$$ \delta _i=\frac{1}{d_i} \sum _{j\in N(i)}(\nu_i-\nu_j) $$

1邻域点加权平均的权有讲究,通常使用 cotangent.

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/