Mesh Generation

Given a fixed point set, Delaunay triangulation will try to make the triangulation more shape regular and thus is considered as a “good” structured mesh.

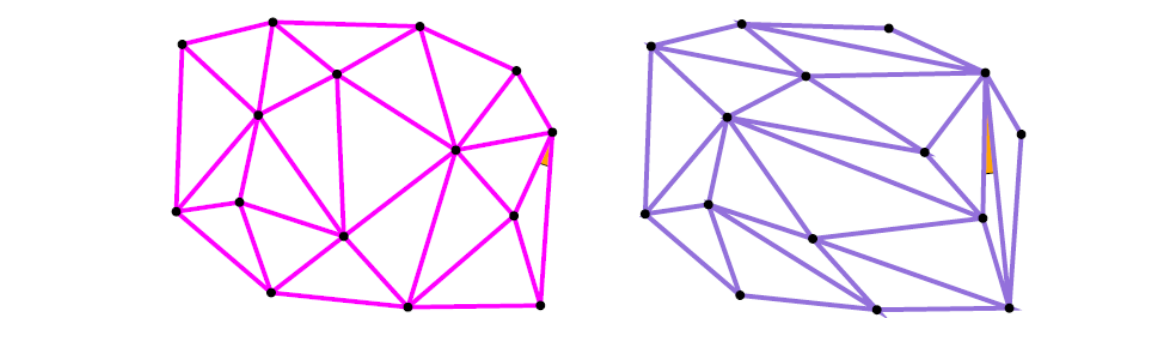
如果点集的位置本身就不好？

👆 The distribution of points is more important for a good mesh.

How to sample points to generate high‐quality meshes?

Centroidal Voronoi Tessellation

定义

定义: The VT is a centroidal Voronoi tessellation (CVT) , if each seed coincides with the centroid of its Voronoi cell

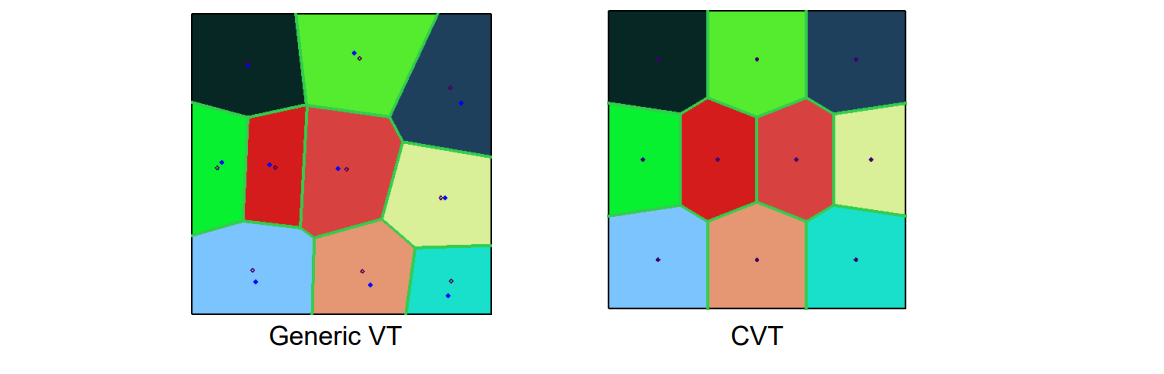
👆 CVT:满是“点与所在区域的重心重合”的 Voronoi 图。

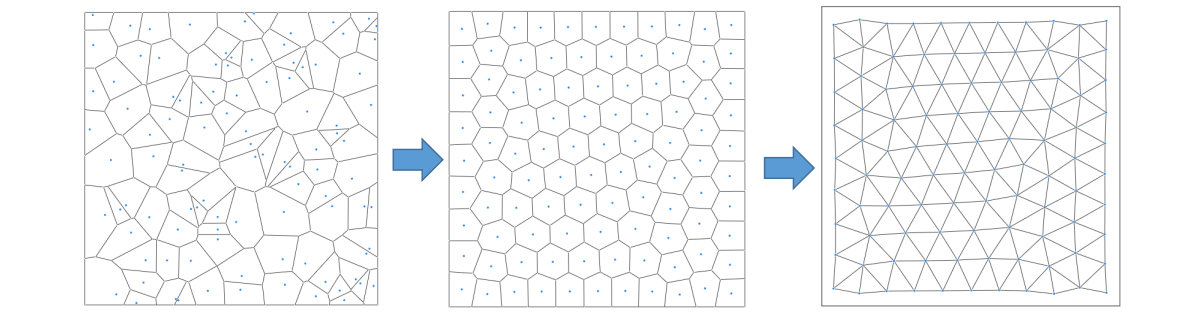
方法

• Construct the VT associated with the points
• Compute the centroids of the Voronoi regions
• Move the points to the centroids
• Iterate until convergent

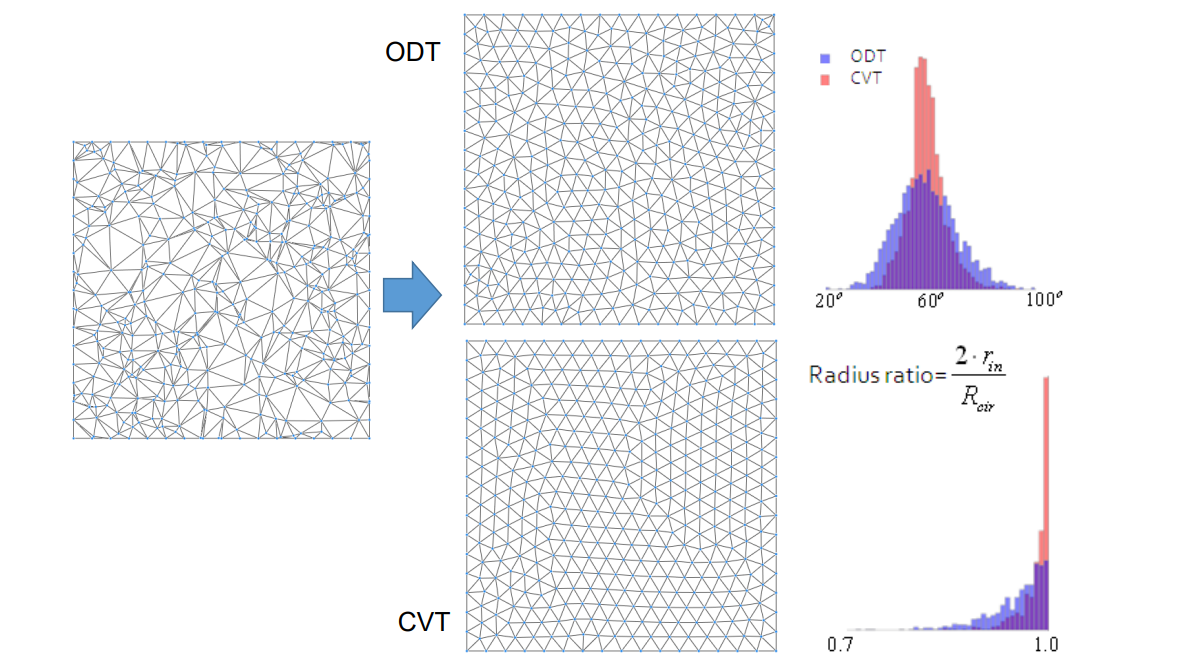
效果

CVT理论

CVT energy function:

$$F(X)=\sum_{i=1}^{N} \int _{V_i}\rho (X)||X-X_i||^2dX$$

CVT is a critical point of $F(X)$, an optimal CVT is a global minimizer of $F(X)$

Geometric interpretation

The CVT energy with $\rho (X)$ identical to 1, is the volume difference between the circumscribed polytope and the araboloid.

$\rho (x)$是种加权，用于内容相关。
当 $\rho =I 时， X为 V_i$的重心时能量最小。

The gradient of $F(X)$ is [Iri et al. 1984; Asami 1991; Du et al. 1999]:

$$\frac{\partial F}{\partial \chi _i} =2m_i(\chi _i-C_i),$$ where $$m_i=\int _{\chi\in \Omega _i }\rho (\chi )d\sigma$$

Lloyd’s method is a gradient descent method, thus has linear convergence

Smoothness of F(X)

Can BFGS method be applied to computing CVT? Or does CVT energy F(X) have required $C^2$ smoothness?

Results:

• It has been noted that F(X) is non‐smooth [Iri et al. 1984], but without proof
• It has been proved that F(X) is $C^1$ [Cortes et al. 2005]
• F(X) is $C^2$ in a convex domain in 2D and 3D [Liu et al. 2009]

C2 Continuity of F(X)

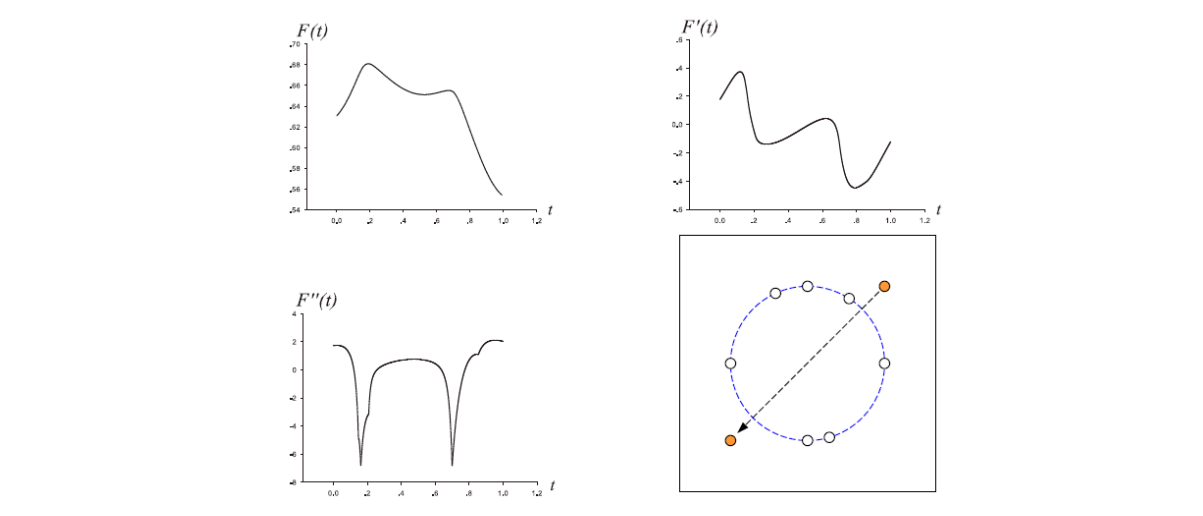
Figure: Illustration of $C^2$ smoothness of CVT energy in 2D

CVT的应用

• CVT on Surface
• CVT for Remeshing

[1:20:59]
把 CVT 算法推广到曲面，可以把距离改为测地线度量
连续曲面测地距离：表面上的孤长
离散网格的测地距离：可参数化到平面再计算

Optimal Delaunay Triangulation

ODT energy function:

$$E(X)=||f-f_{I,T }||L^1(\Omega)$$

$$=\sum _{\tau \in T}\int _\tau f_I(X)dX-\int _\Omega f(X)dX$$

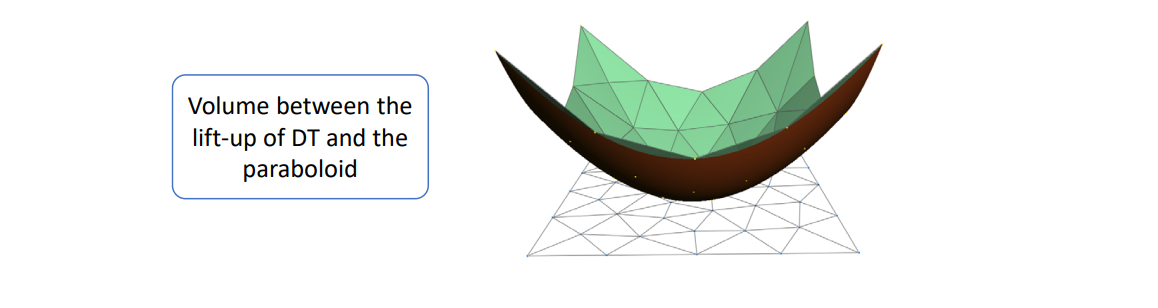
CVT VS ODT Energy

• CVT energy

$$F(X)=\sum _{i=1}^N\int _{V_i}||X-X_i||^2dX$$

• ODT energy

$$E(X)=\sum _{\tau \in T}\int _\tau f_I(X)dX-\int _\Omega f(X)dX$$

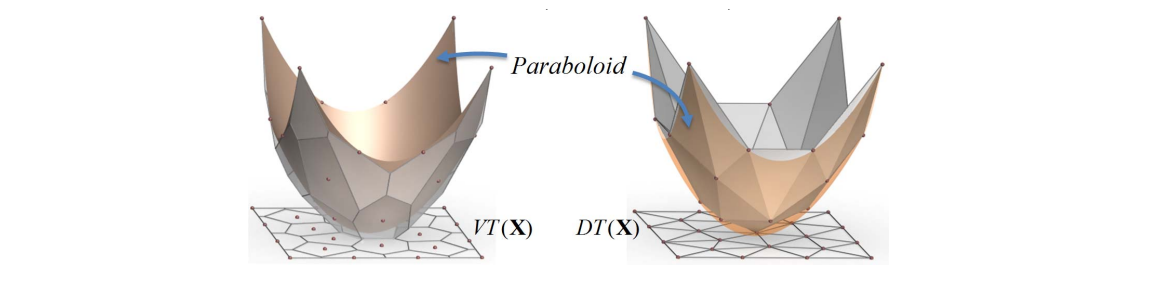
比较：

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/