从连续到离散

对象的表达
• 在数学上，连续表达与计算
• 在计算机中，离散表达与计算
数值方法：数值微分、数值积分、数值优化
• 数值分析：离散计算对精确计算的近似程度
• Fourier分析/变换：离散Fourier分析/变换
• 卷积（滤波）
在计算机科学（计算机图形学）中，采样无处不在
• 计算机只能表达离散的数值
• 例子：int型的数据（量化）

💡 人的感知精度高，宏观表现为连续，计算能力支持的精度低，宏观表现为离散，精度不匹配就会产生artifact.

曲线的离散化

要解决的问题

将连续性表达转化为多边形表达（分段线性）

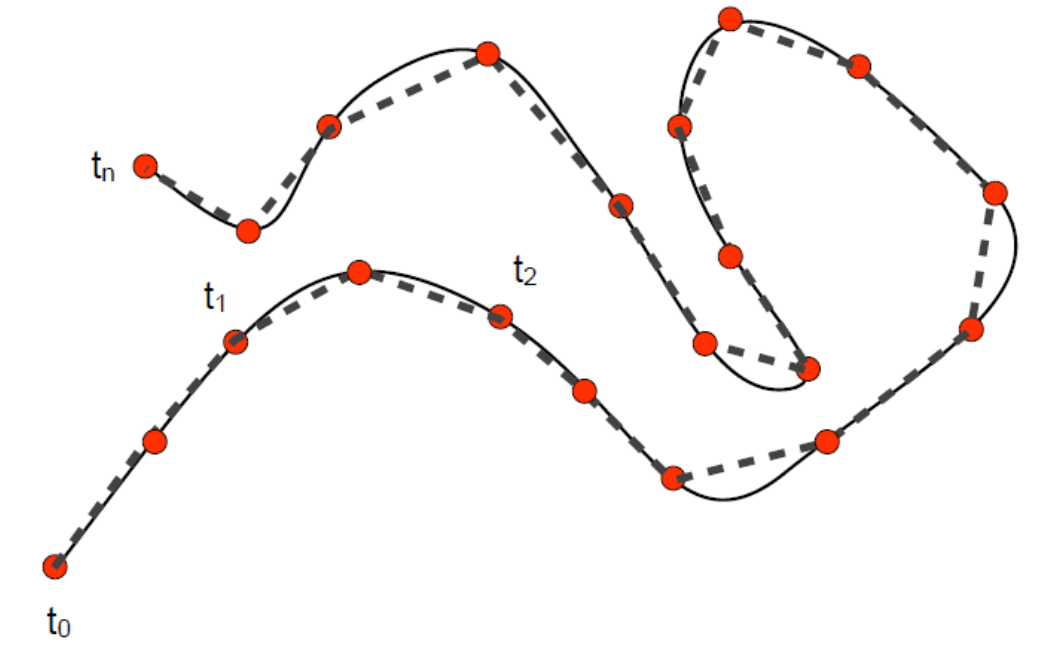
黑色是光滑曲线，但无法用于计算。因此用虚线近似替代曲­线进行计算。只要能控制直线与曲线的误差。

为何要离散化？

• 渲染的必要性：线段/圆的光栅化

  • 曲线的绘制：曲线须离散成多边形
  • 曲面的绘制：曲面须离散成三角形网格
    

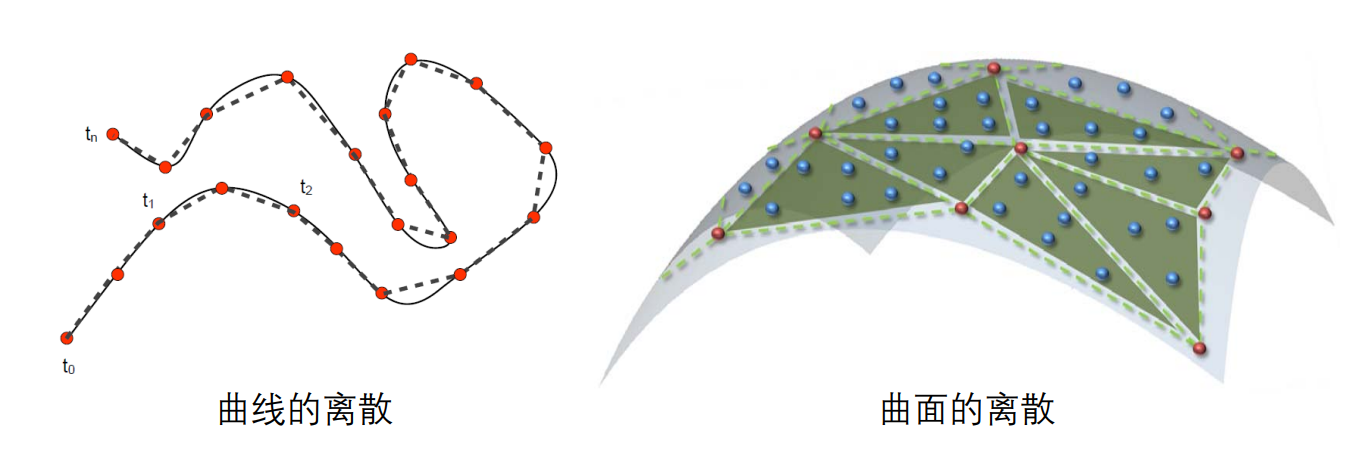
只有针对线段或特殊曲线（圆、椭圆）等的高效渲染算法。
不会针对一般曲线专门设计，因此要把一般曲线离散成线段再渲染。

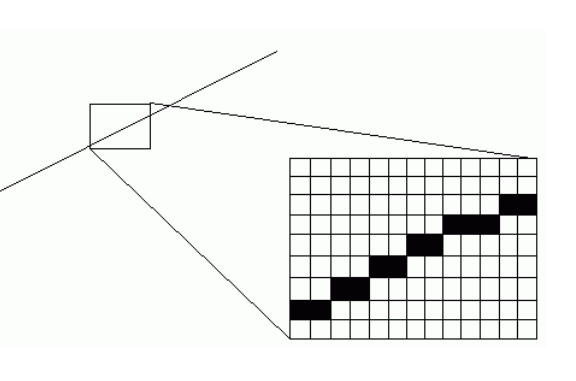
• 计算的必要性：直线求交、多项式求根

• 制造的必要性：刀具轨迹只能走直线段和圆弧

Nyquist–Shannon采样定理

If a function \(x(t)\) contains no frequencies higher than B hertz, it is completely determined by giving its ordinates at a series of points spaced 1/(2B) seconds apart.

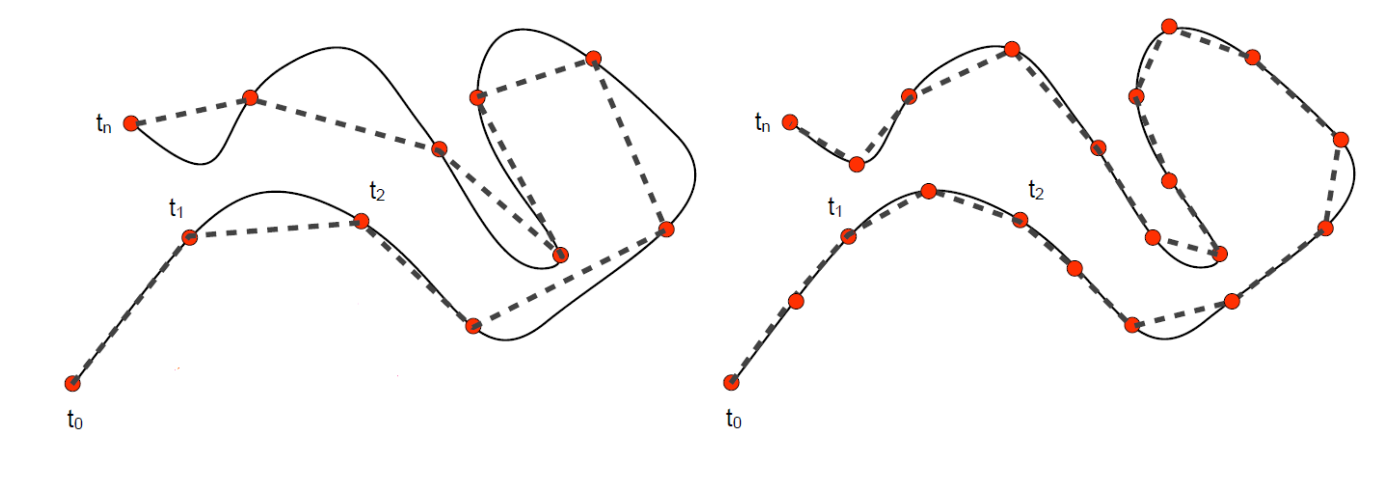
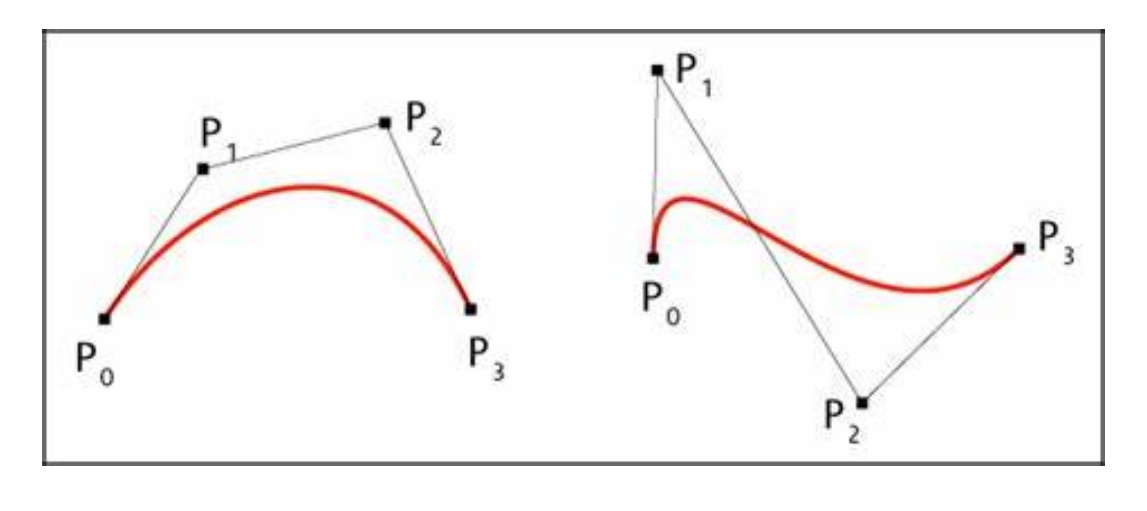
Bezier曲线的离散定理

定理：曲线到弦的最大距离<控制顶点到弦的最大距离
应用：给定误差，估计离散层级

离散曲线的几何量的计算

• 如果有连续表达，利用连续表达的曲线来计算

• 如无连续表达
  • 差分法：利用差分形式来近似微分属性

差分法：一个点的导数是相邻点的差分，用前一点和后一点的弦的斜率来代替当前点的切线。

• 拟合法：利用光滑函数来拟合估计属性

• Tylor展开及估计

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/