重心坐标要解决的问题 - FFD

FFD = Free‐form Deformation

[Sederberg et al. 86]

问题：给定一个包含物体的边界多边形，改变边界时，如何计算物体的变形？
方法：Embed the object into a domain that is more easily parametrized than the object.

优点:
• You can deform arbitrary objects
• Independent of object representation

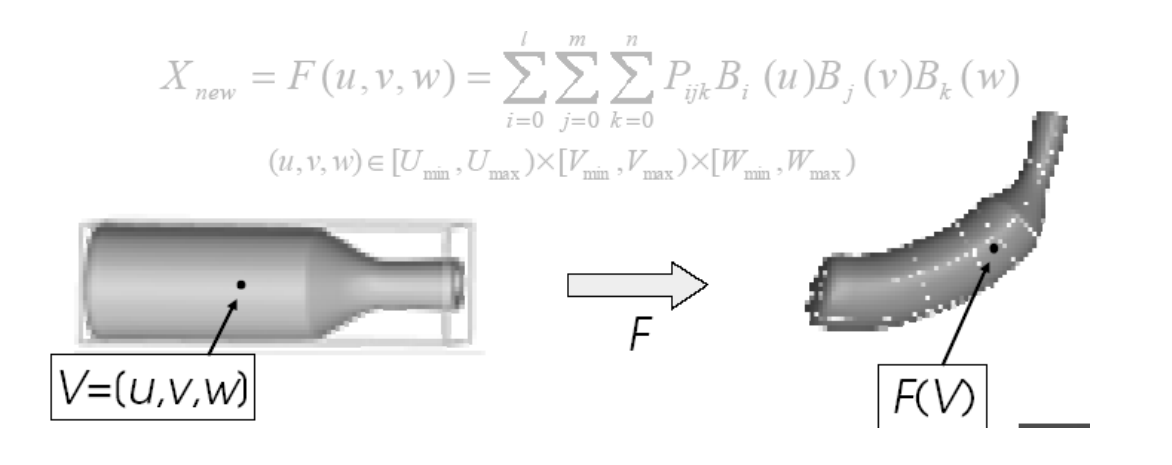
本文是作用于3D物体的算法，以2D为例说明该算法：
用 Bezier 面片包围目标面片。通过控制 Bazier 顶点来控制目标面片。
Bezier 顶点称为 proxy （代理） ，但Proxy 不一定是 Bezier 点，也可以是边界上的点，主要是找到目标上任意一个点与 Proxy 点之间的关系。
因此问题简化为求内部点与边界点（控制顶点）之间的关联关系
关联关系本质是重心坐标，即组合系数
代理的优点是：简化问题，可以快速得到一个基本准确的结果。
缺点是：1.有些无法简化的地方，就是artifact.
2.如何得到准确的关联关系。

几何图形的重心坐标

三角形的重心坐标：三角形的顶点是 Proxy 点. P是三角形内任意一点。用某种方法来描述P与 Proxy 点之间的关系。

即把P描述为Proxy点的线性组合。线性组合的系数就是P的重新坐标值。

四边及以上多边形不能用三角形的方法求重心坐标，因为系数解不唯一。
因此需要一种对所有多边形适用的更统一的重心坐标定义方式。

Coordinates：这一页没讲
重心坐标的应用：这一页没讲
Coordinates In A Polytope：这一页没讲
BC of 2D Polygons：这一页没讲

各种重心坐标的计算方法

• Wachspress (WP) coordinates

$$ w_{i}=\frac{\cot \gamma_{i-1}+\cot \beta_{i}}{r_{i}^{2}} $$

• mean value (MV) coordinates

$$ w_{i}=\frac{\tan \left(\alpha_{i-1} / 2\right)+\tan \left(\alpha_{i} / 2\right)}{r_{i}} $$

• discrete harmonic (DH) coordinates

$$ w_{i}=\cot \beta_{i-1}+\cot \gamma_{i} $$

不同的几何坐标都有相应的几何背景

重心坐标的应用

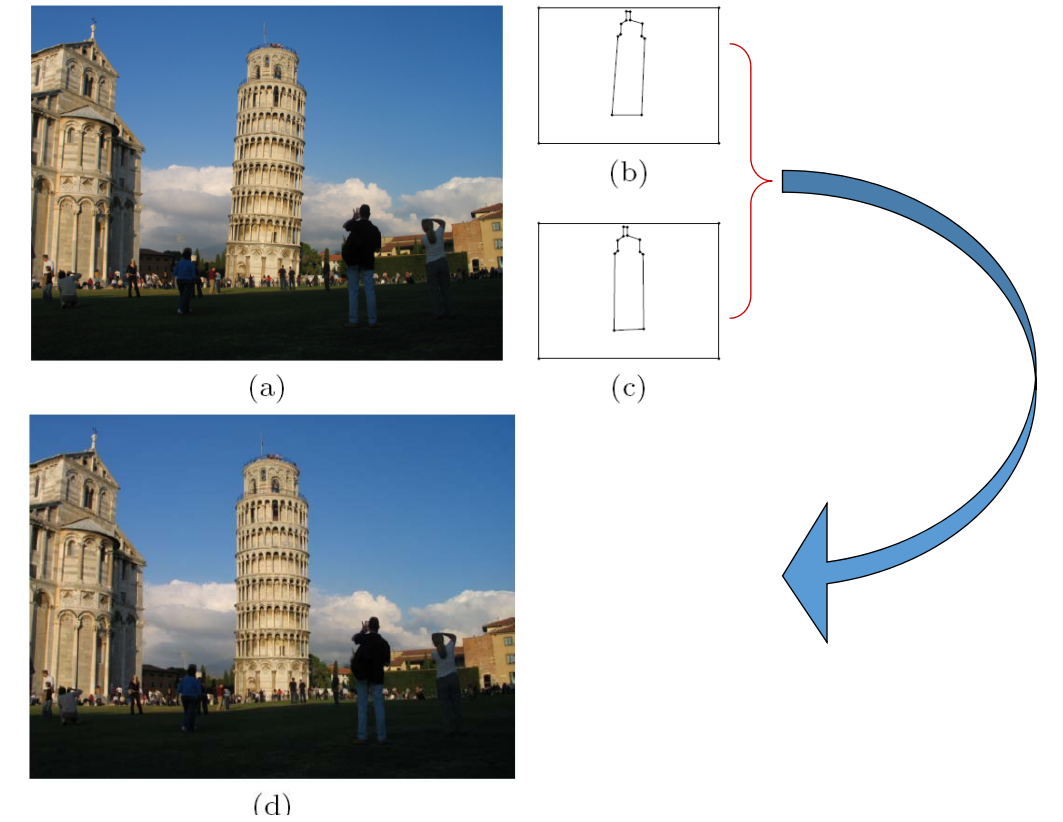
1.imge warping

2. shading

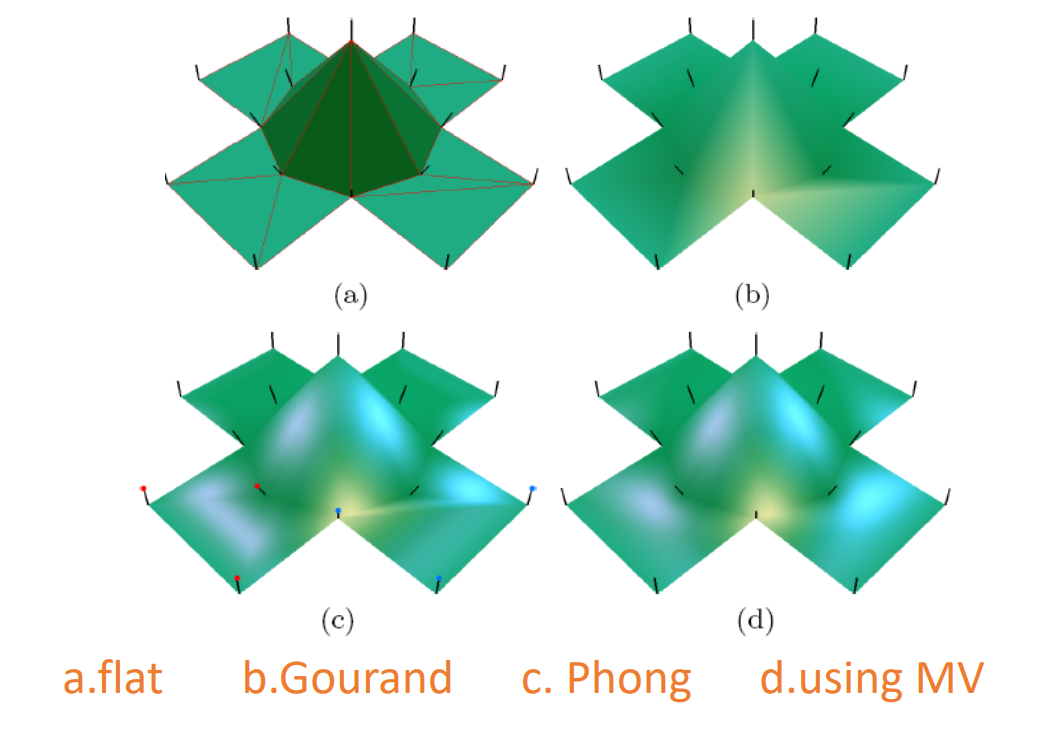
通常只存储顶点上的shading value. 非顶点处的shade value 是通过顶点的shading value 插值得到。插值是基于重心坐标做的。

3. Transfinite Interpolation

问题：给定4条边界曲线，构造插值这4条曲线的一张曲面

Interpolating height function to model a surface

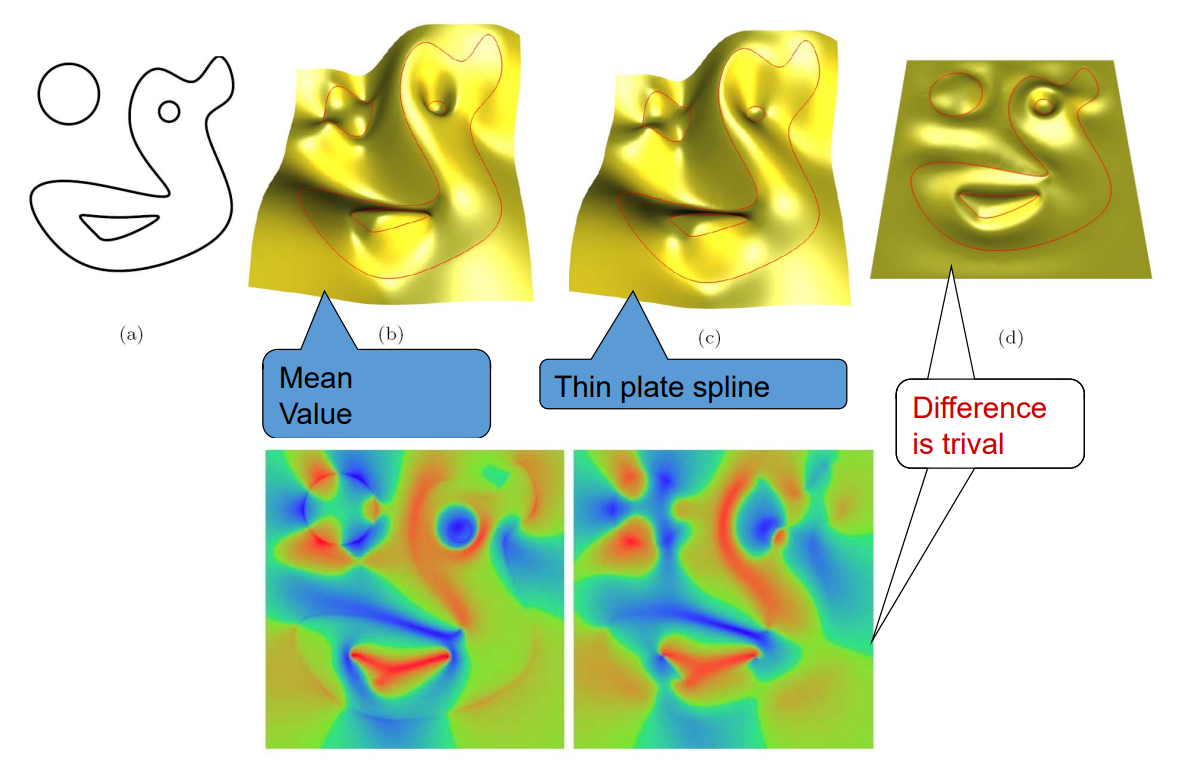
4. allow directly updating on interpolation when resampled.

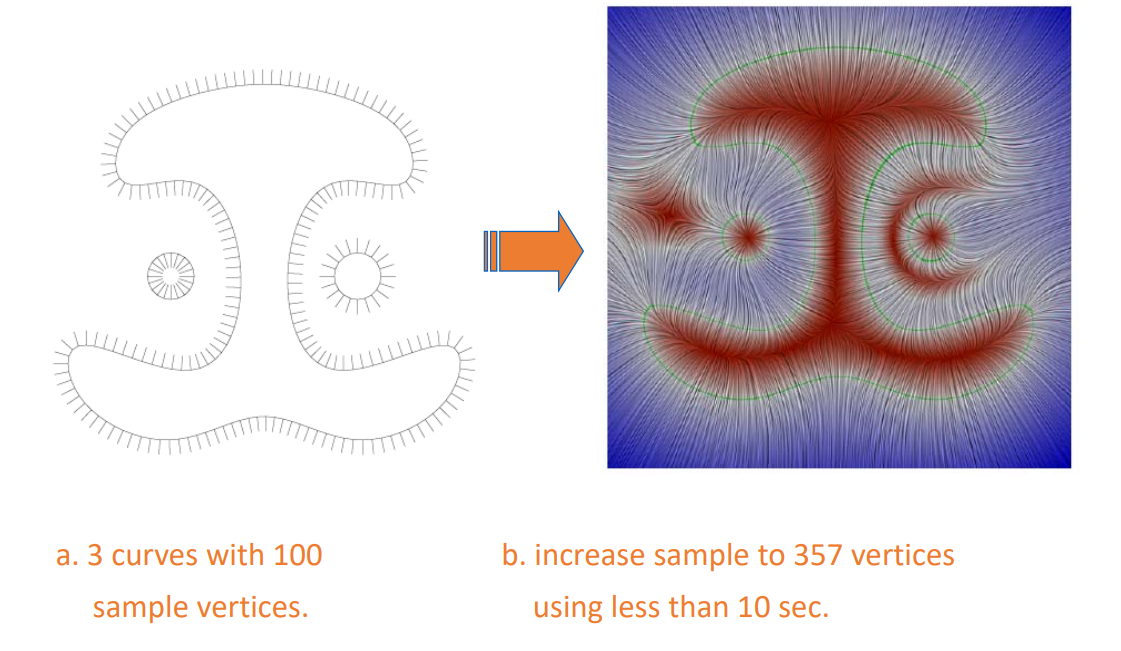
❓ 这就是普通插值，跟重心坐标有什么关系？

广义重心坐标的学习资料

http://www.inf.usi.ch/faculty/hormann/barycentric

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/