Local Laplacian Smoothing的作用

几何细节的度量

Useful for operations on surfaces where surface details are important

Laplacian Smoothing

方法

$$ P^{new}=P^{old}+\lambda L(P^{old}) $$

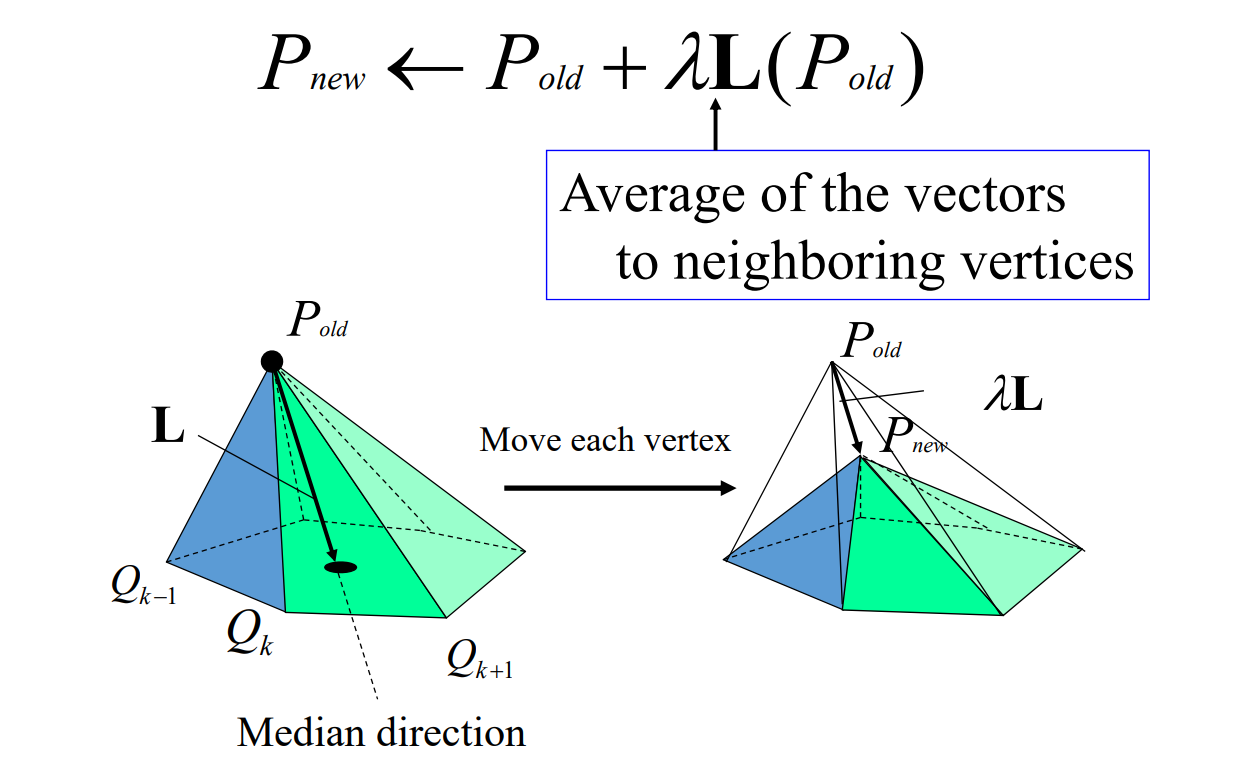
上节课的任意曲面到极小曲面的过程,是一种特殊的Local Lapluàn Smoothing.
也可以看作是去噪、滤波。

平滑也相当于滤波，GAMES101有解释。

over-smoothing问题

但存在over-smoothing问题，需要选择合适的\(\lambda\)和迭代次数。

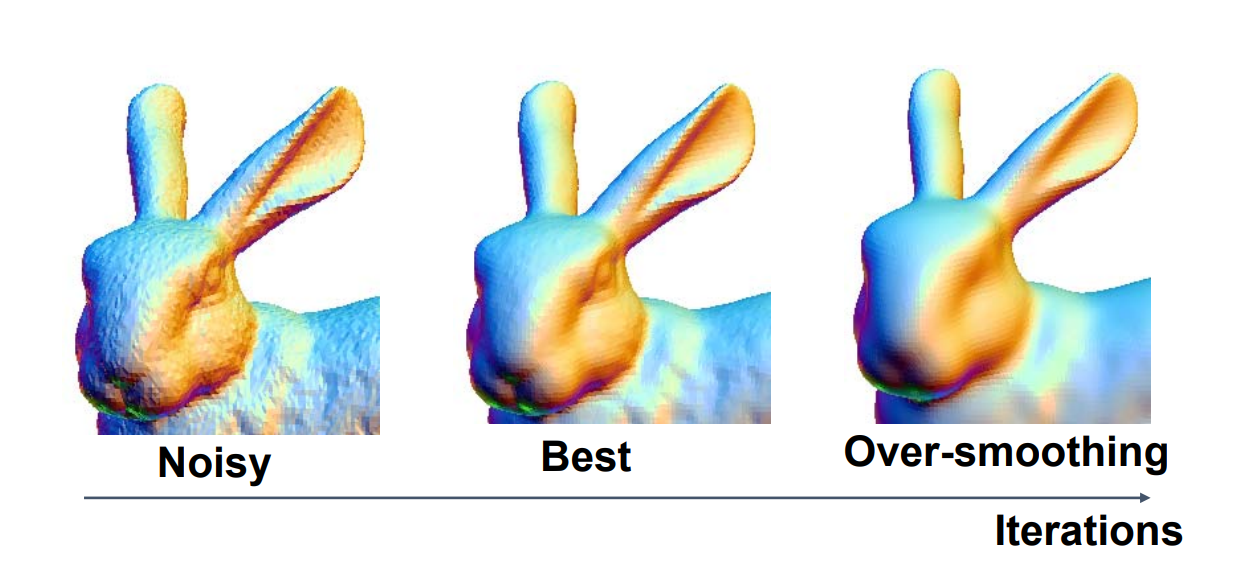
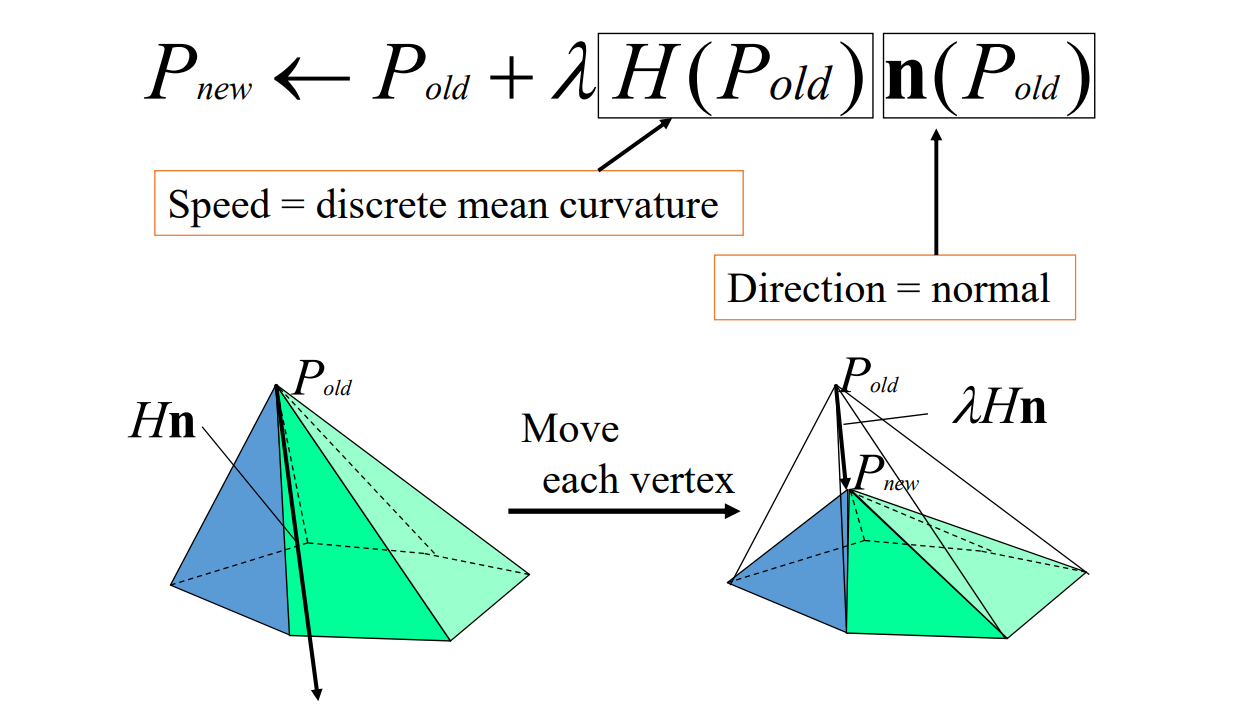
基于平均曲率流近似Laplacian Smoothing的效果

平均曲率流：link

不知道拉普拉斯坐标，但知道平均曲率和法向，也能做拉普拉斯平滑
Laplacian 可以用于提取高频和平滑高频，效果取决于权重定义是否合理。

$$ Hn=\frac{\nabla _PA}{2A} $$

$$ Hn=\frac{1}{4A} \sum _j(\cot \alpha _j+\cot \beta _j)(P-Q_j) $$

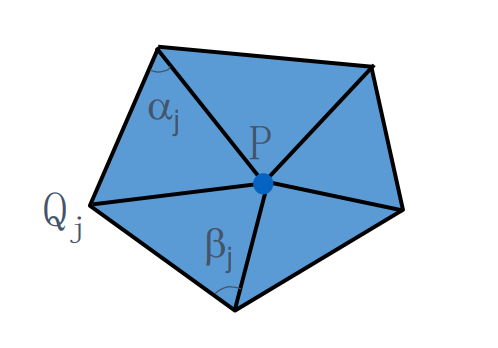
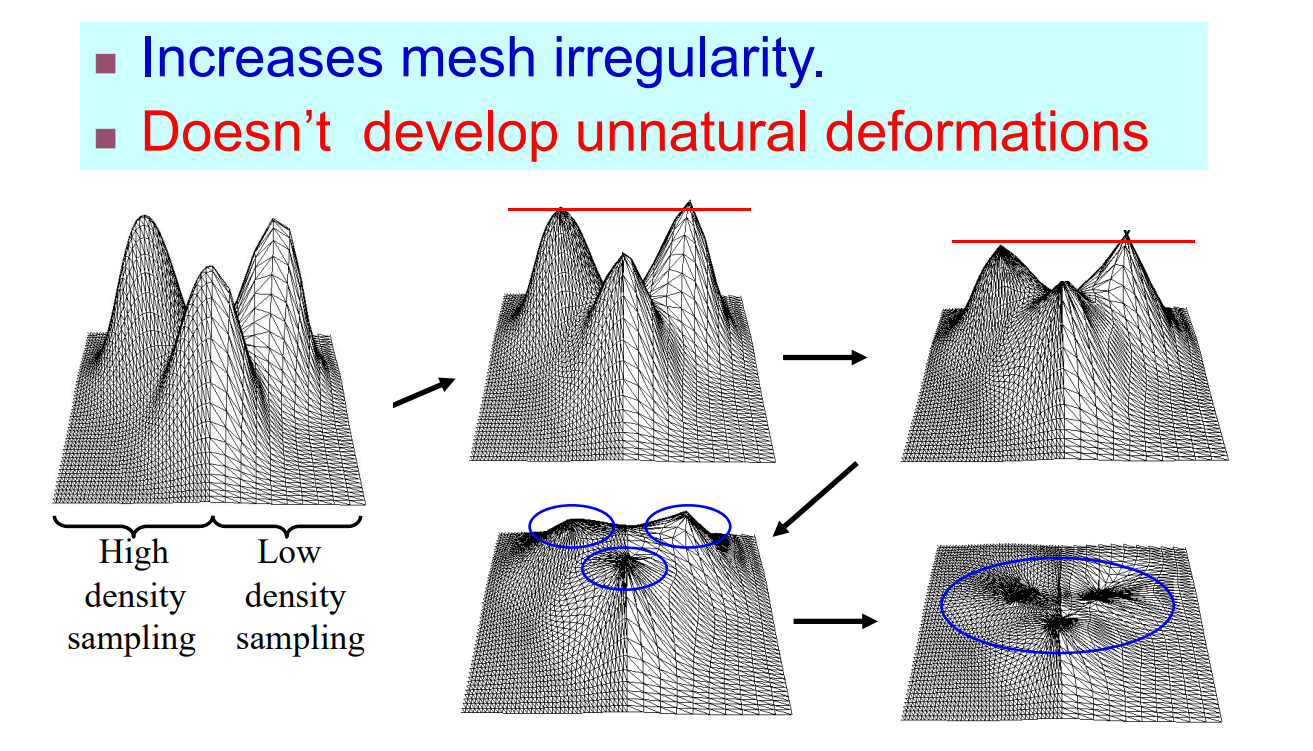
Mean Curvature Flow 使用 cotangent 权，因此是Laplacian Smoothing 的特殊形式。
对于 low densily mesh,\(\delta _i\) 比较长，如果使用普­通权，这种情况会收缩快。如果使用 cotangent 权，则不会。

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/