Delaunay三角化

[1:06:28] 一种点云剖分算法

剖分结果

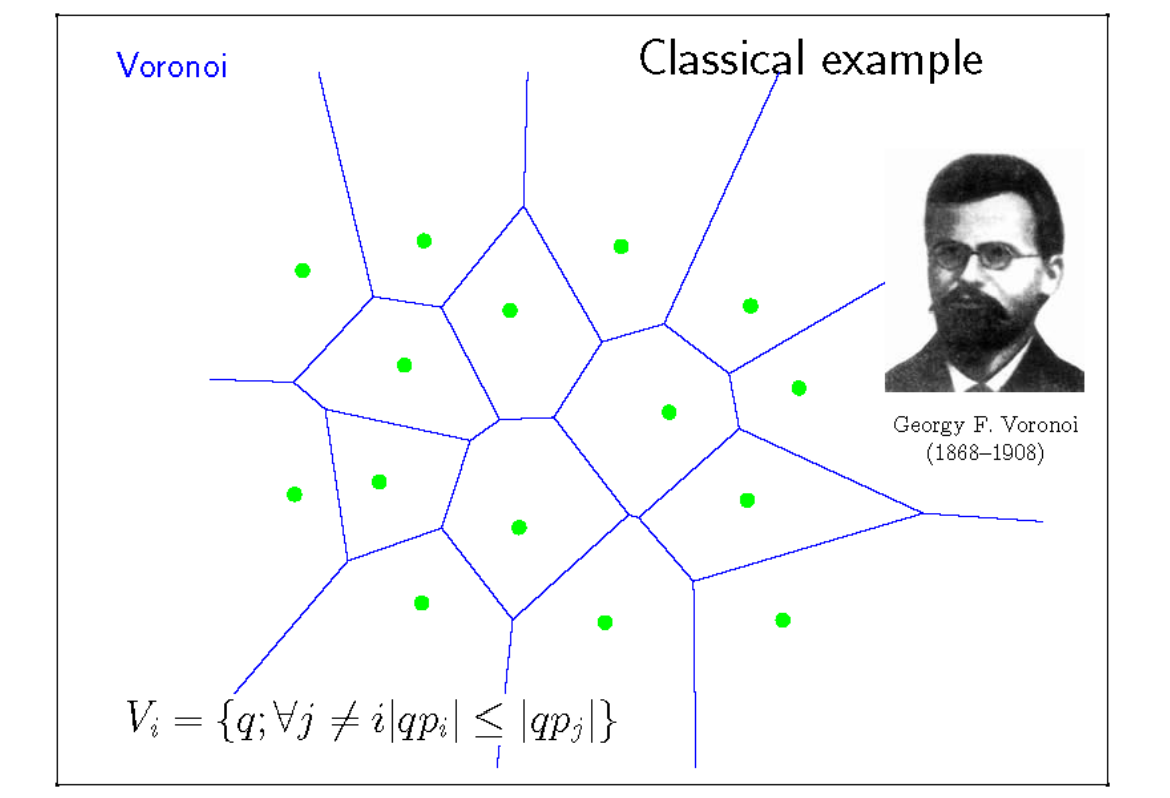
绿点：点云、平面上的点

(1) 给每个点一个区域，区域的边界由两个绿点的中垂线构成。（蓝线图）
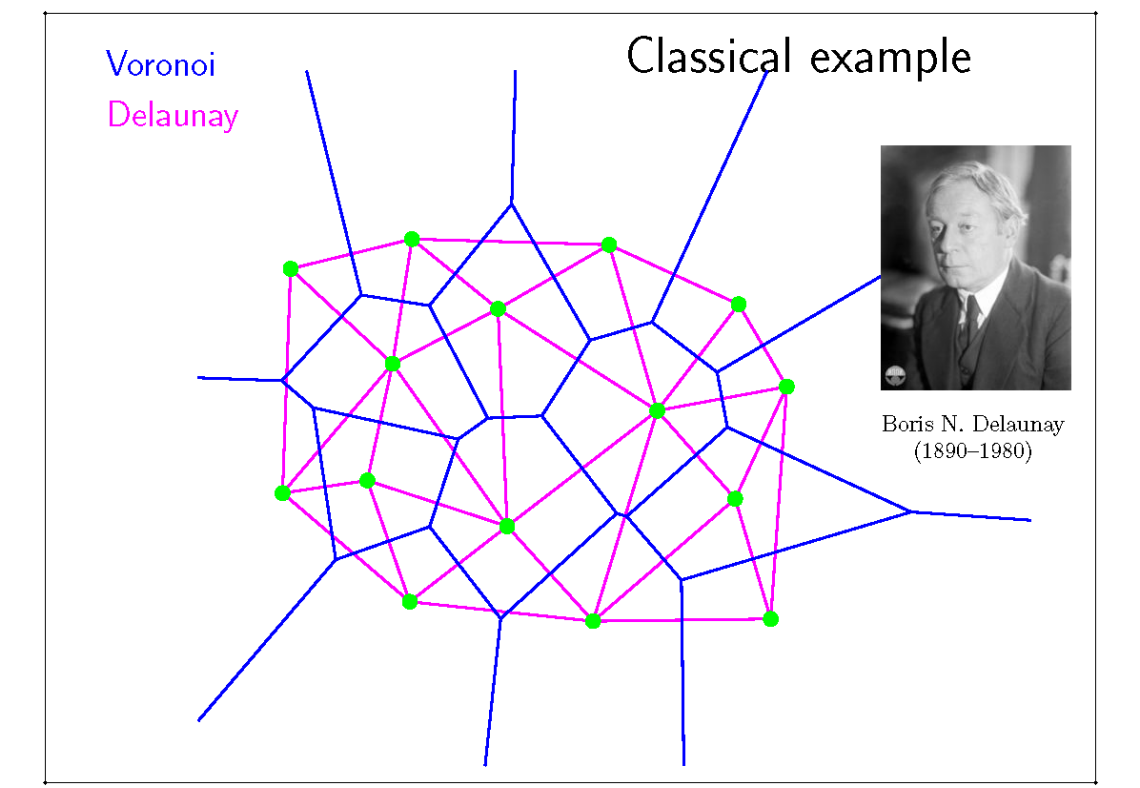
(2) 红线图为蓝线图的对偶图
[?] 什么是对偶图？边对边、面对点是什么意思？
以图上观察是，点所属区域有几个边，点就会发出多少连线，连线的另一端是区域边界对应的点。

具体过程

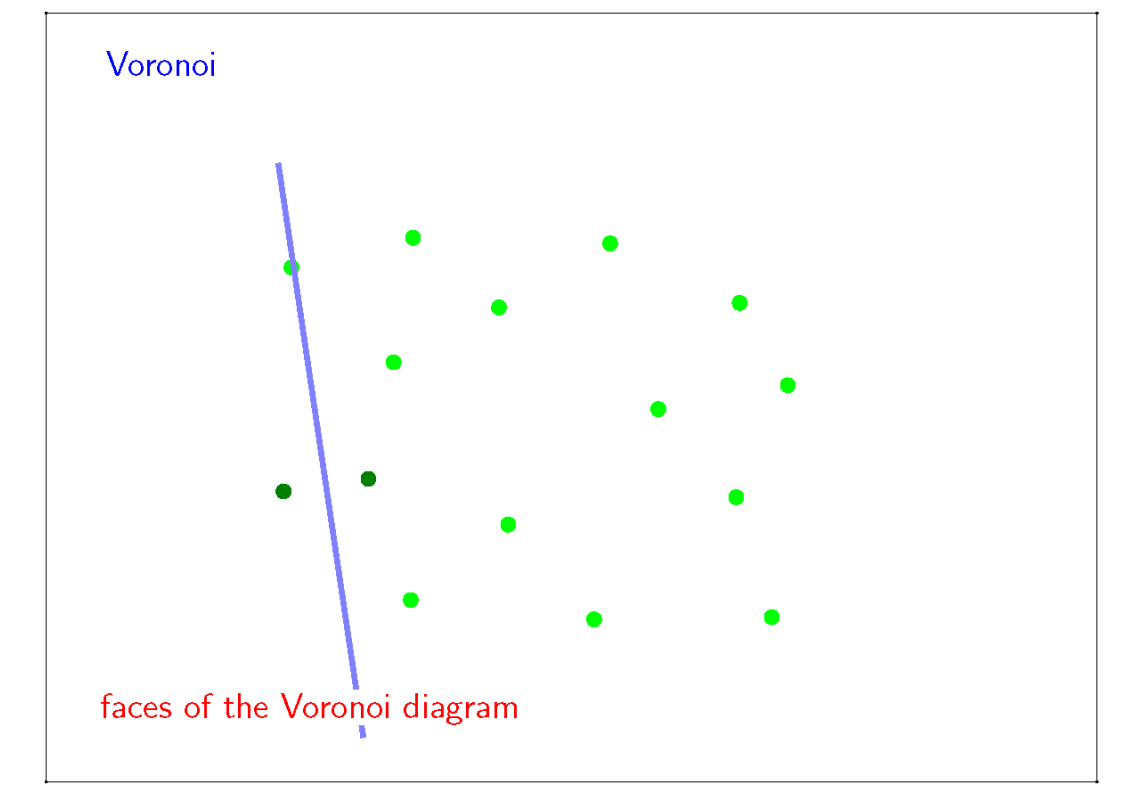
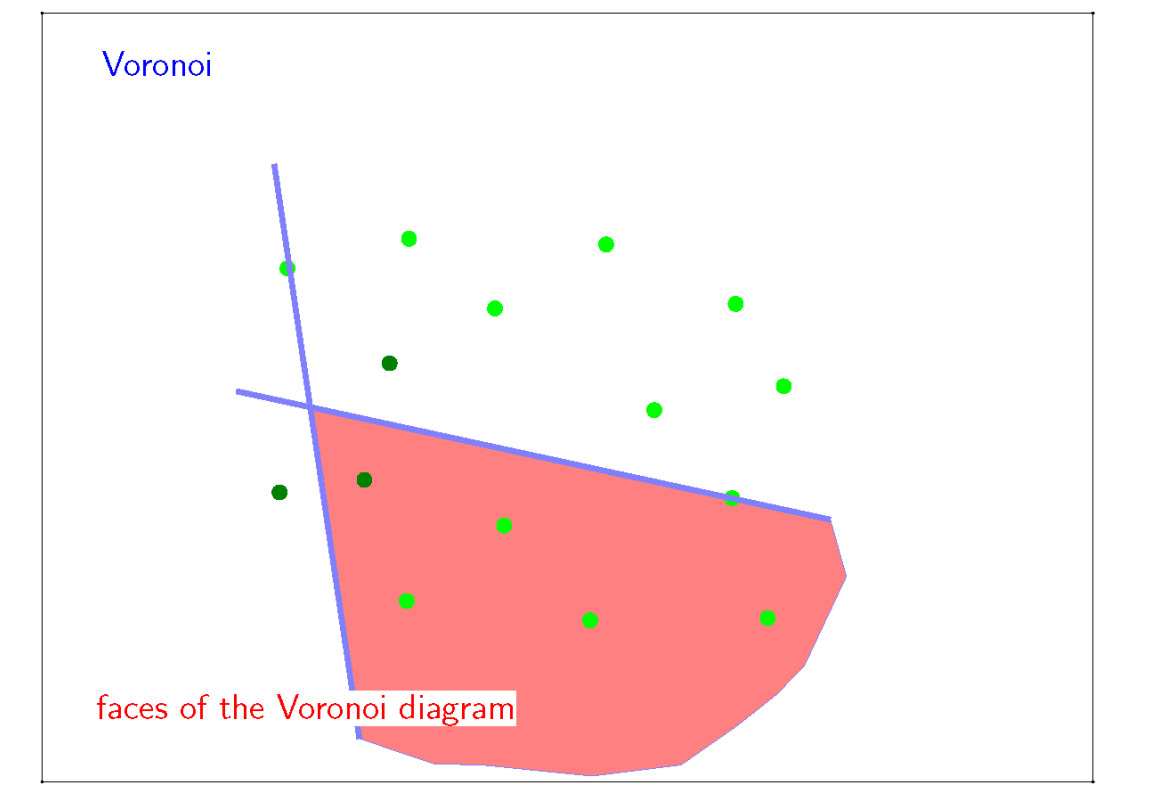
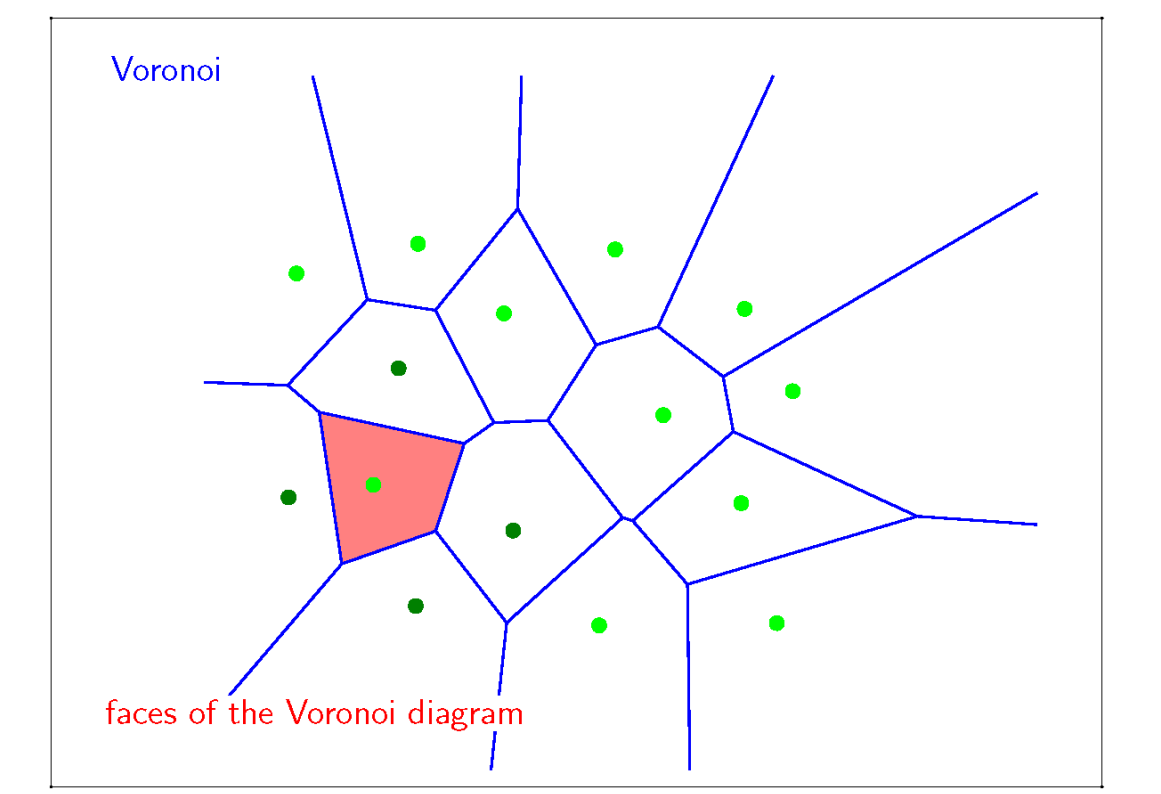
(1)图称为 Voronoi 图
(2)图称为 Trangulation 图

Properties of DT

DT: Delaunay Triangulation

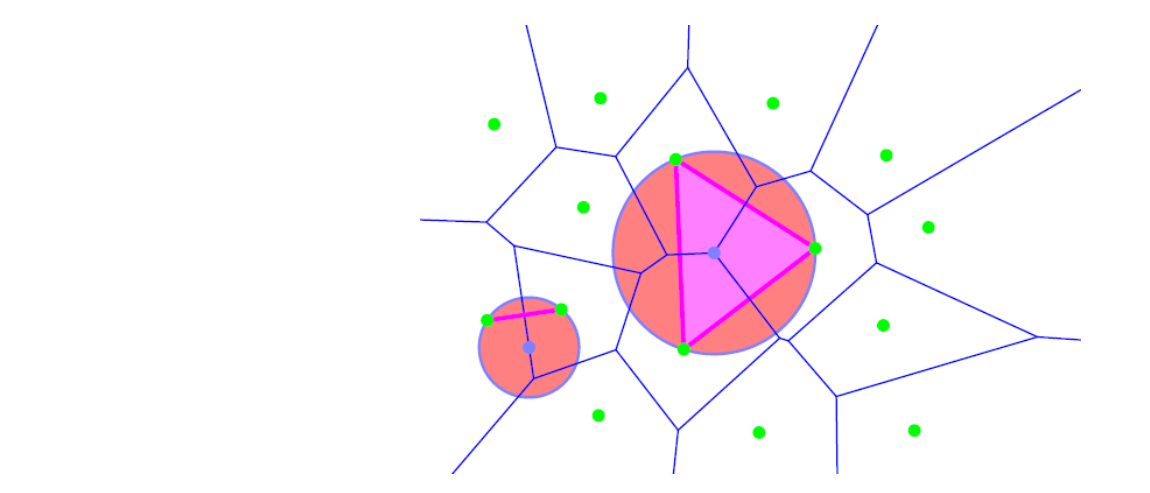
空圆性质

Empty sphere property: no points inside the circum‐sphere of any simplex

空圆性质：三角形外接圆一定不含其它绿点（四点共圆除外）

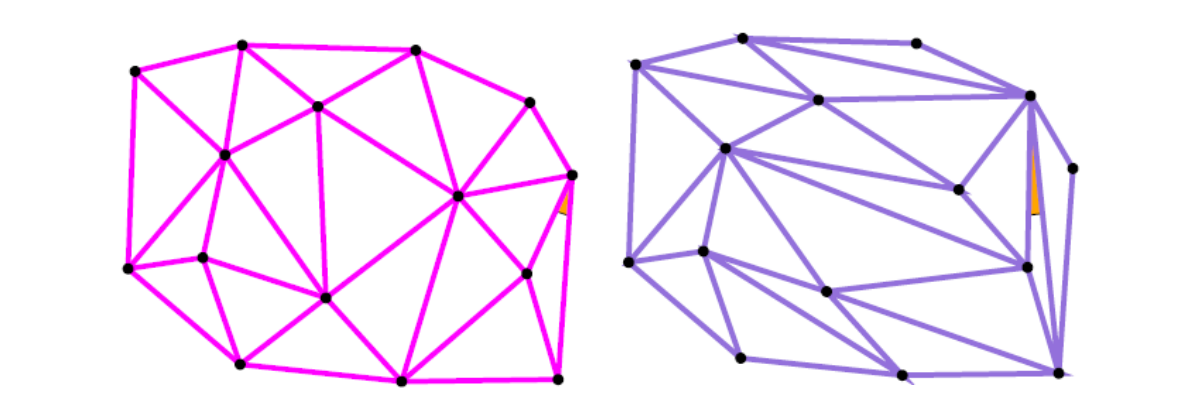
最小角最大

最小角是指：所有三角形中最小的角
最大是指：所有可能的三角化方法中，此方法的最小角最大。

[Lawson 1977] and [Sibson 1978]

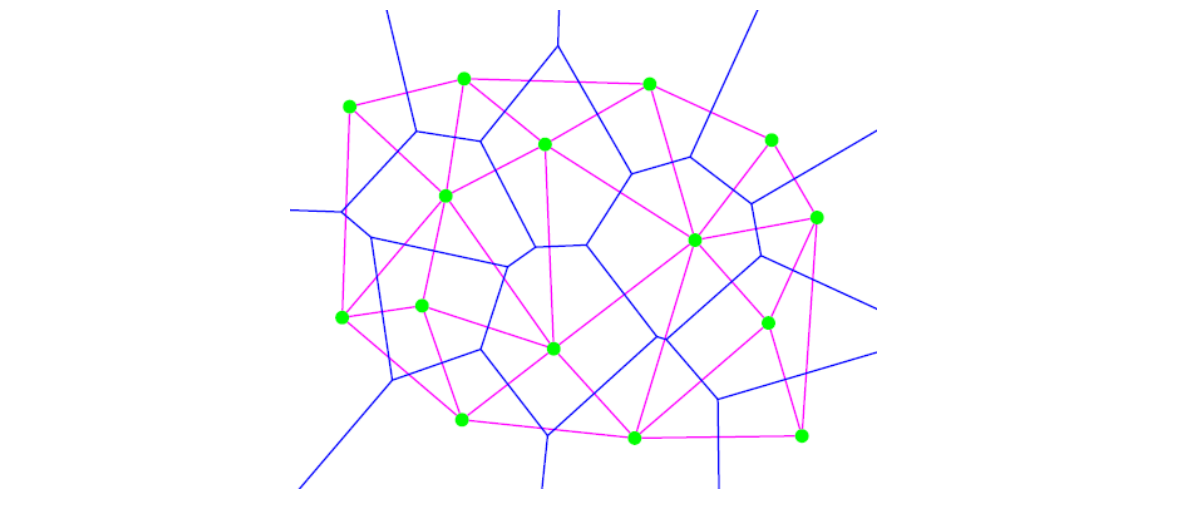
凸包

三角形最外层边是点集的凸包

其它

• DT maximizes the arithmetic mean of the radius of inscribed circles of the triangles.
  • [Lambert 1994]
• DT minimizes roughness (the Dirichlet energy of any piecewise‐linear scalar function)
  • [Rippa 1990]
• DT minimizes the maximum containing radius (the radius of the smallest sphere containing the simplex)
  • [Azevedo and Simpson 1989], [Rajan 1991]

Edge Swapping/Flipping [Sibson 1978]

这是一个求Delaunay的方法

1. Start with any triangulation
2. find any two adjacent triangles that form a onvex uadrilateral that does not satisfy empty sphere condition
3. swap the diagonal of the quadrilateral to be a Deluany triangulation of that four points
4. repeat step 1,2 until stuck.

优点：简单、直观、必定收敛。
缺点：慢、不可并行。

Algorithms for Voronoi Diagrams

这是一个求Voronoi的方法

• Compute the intersection of n‐1 half‐planes for each site, and “merge” the cells into the diagram
• Divide‐and‐conquer (1975, Shamos & Hoey)
• Plane sweep (1987, Fortune)
• Randomized incremental construction (1992, Guibas, Knuth& Sharir)

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/