隐式曲线

回顾：参数曲线

曲线定义在一个单参数$t$的区间上，有$t$上的基函数来线性组合控制顶点来定义

$$x(t)=\sum_{i=0}^{n} B^n_i(t)b_i$$

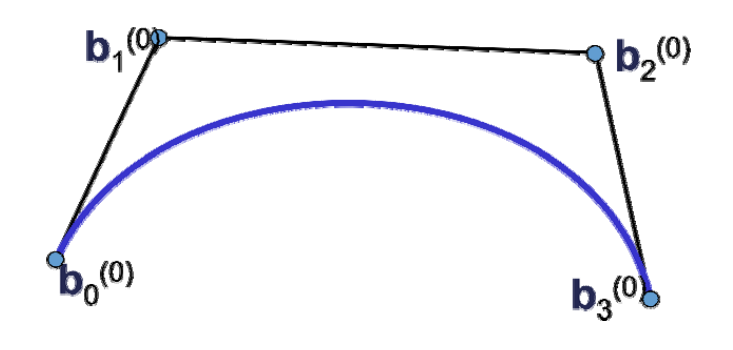
曲线的性质来源于基函数的性质

回顾：平面曲线的定义方法

显式函数

$$f:R^1\longrightarrow R^1$$

$$y=f(x)$$

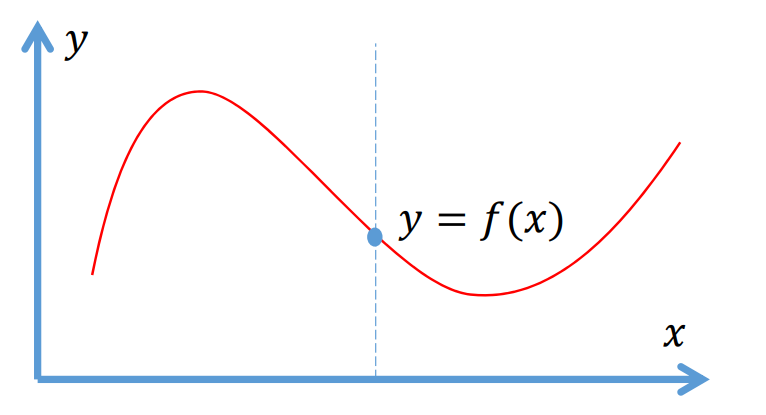
👆 点$(𝑥,𝑓(𝑥)),𝑥∈[a,b]$的轨迹

参数曲线

$p:R^1\longrightarrow R^2$
$x=x(t)$
$y=y(t)$

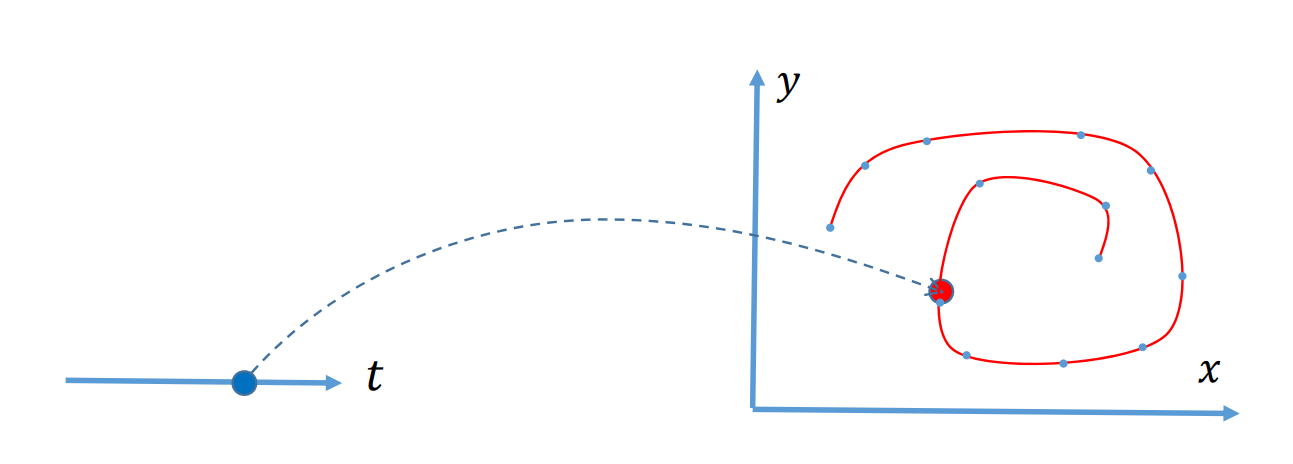
👆 点$(𝑥(𝑡),𝑦(𝑡)),𝑡∈[𝑎,𝑏]$的轨迹

隐式函数

自变量$x$和应变量$y$的关系非显式关系，是一个隐式的关系（代数方程）：

$$f(x,y)=0$$

比如：
• $𝑎𝑥+𝑏𝑦+𝑐=0$
• $𝑥^2+𝑦^2=1$
• $𝑦^2=𝑥^3+𝑎𝑥+𝑏$
• $𝑥𝑦^2+\ln(𝑥$ $\sin 𝑦-𝑒^{y-\sqrt{x} })=\cos (x-\sqrt{x^3-2y} )$

所有满足该代数方程的点的轨迹是条曲线

细分曲线

前三种是连续表达，第四种是线段表达。
连续表达在数学上容易表达。但在应用上有局限。

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/