Laplacian Editing

[Sorkine et al. SGP 2004]

What’s are Details?

• Detail = surface – smooth (surface)
• Smoothing = averaging

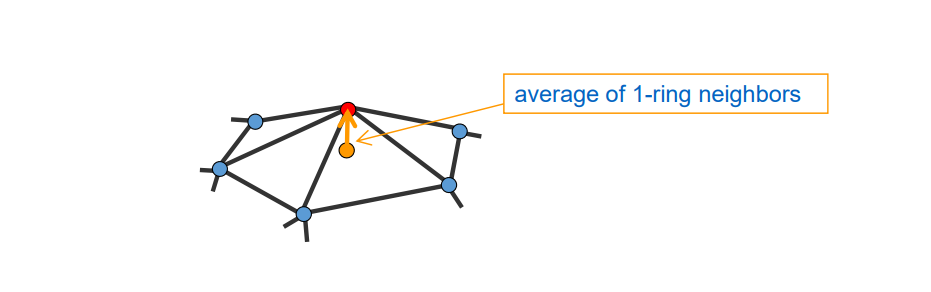
What’s the Difference?

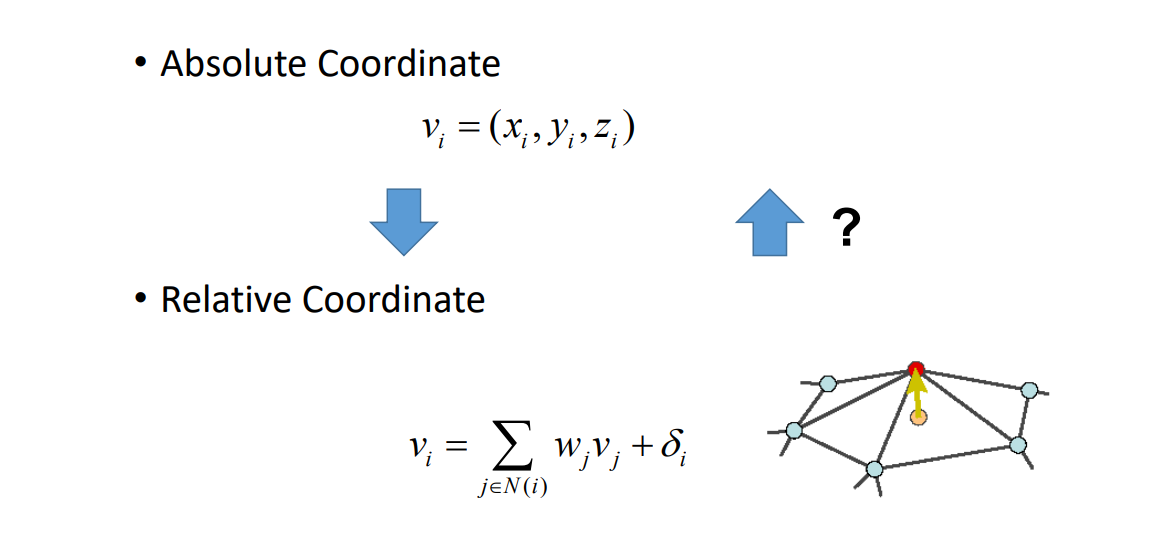
Laplacian Editing

• Local detail representation – enables detail preservation through various modeling tasks
• Representation with sparse matrices
• Efficient linear surface reconstruction

Editing framework

• The spatial constraints will serve as modeling constraints
• Reconstruct the surface every time the modeling constraints are changed

Detail constraints: $LX=\delta$
Modeling constraints: $x_j=c_j,j\in$ {$j_1,j_2,\dots j_k$}

用户对 mesh 的一个点进行编辑，算法更新其他的点，得到合理结果。
本质：保持 mesh 的 Laplace 不变，因为 Laplace 描述了曲面的特征。
准确说是 Laplace 长度不变，方向有可能旋转。

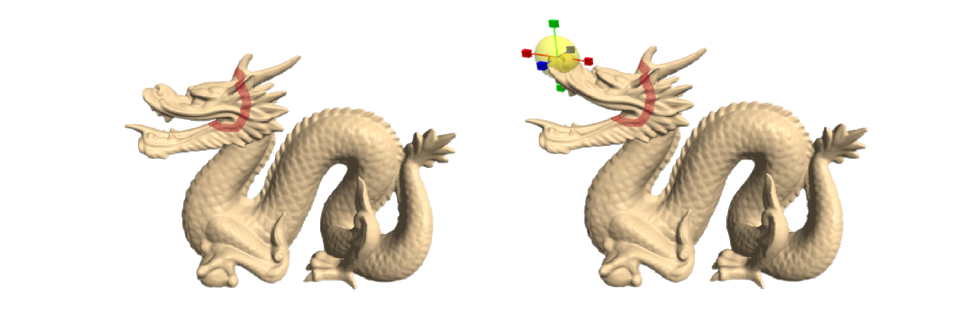
Direct Detail Preserving

Rotation Transformation

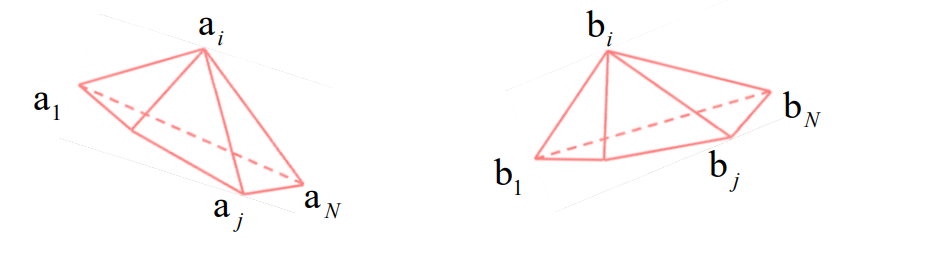
$$\begin{pmatrix}b_1-b_i  \\\vdots  \\b_N-b_i \end{pmatrix}=\begin{pmatrix}a_1-a_i  \\\vdots  \\a_N-a_i \end{pmatrix}R_i$$

Reconstruction

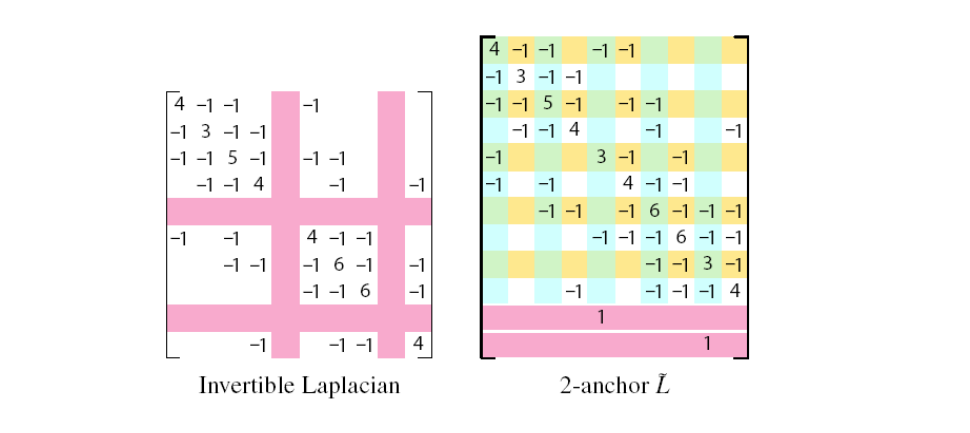
• Soft constraints

$$L^TLv=L^T\delta$$

Variational Viewpoint

• Laplacian Approximation

$$\tilde{X} =\underset{X}{argmin} (||LX-\delta ^{(x)}||^2+\sum _{j\in C}w^2||x_j-c_j||^2).$$

• Gradient Approximation

$$\underset{\phi }{min} \iint _\Omega ||\nabla \phi -w||^2dA,$$

User Interfaces

• ROI is bounded by a belt (static anchors)
• Manipulation through handle(s)

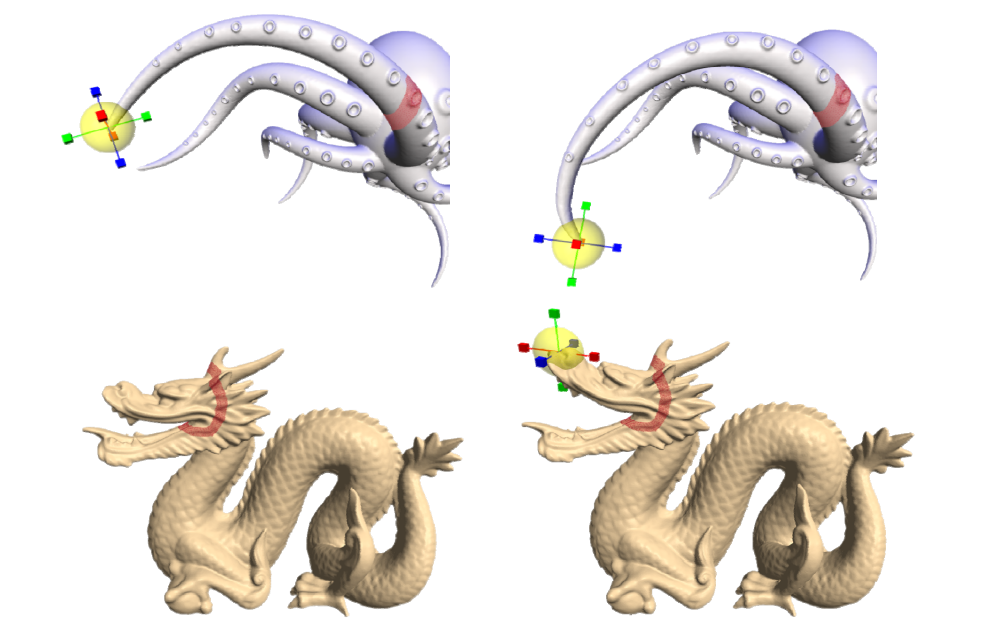
Results

Detail transfer and mixing

• “Peel“ the coating of one surface and transfer to another

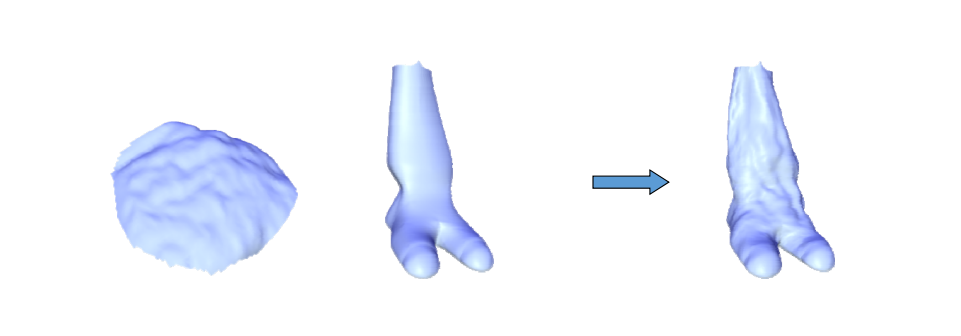
第一步：Parameterization onto a common domain and elastic warp to align the features, if needed

第二步：Detail peeling:

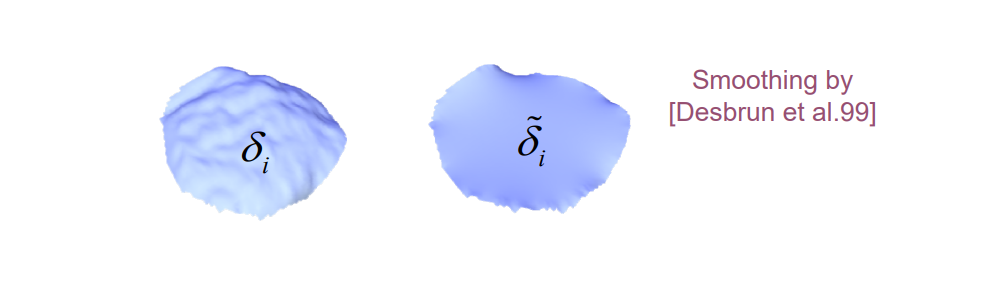
$$\xi _i=\delta _i-\tilde{\delta } _i$$

第三步：Changing local frames:

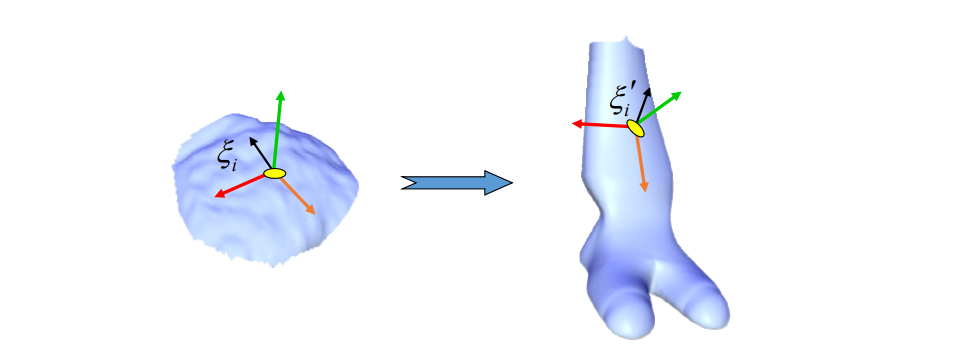
第四步：Reconstruction of target surface from: $\delta _{target}$

$$\delta _{target} ={\delta}' _i+{\xi}' _i$$

Examples

Mixing Laplacians

• Taking weighted average of $\delta _i$ and $\delta ^‘_i$

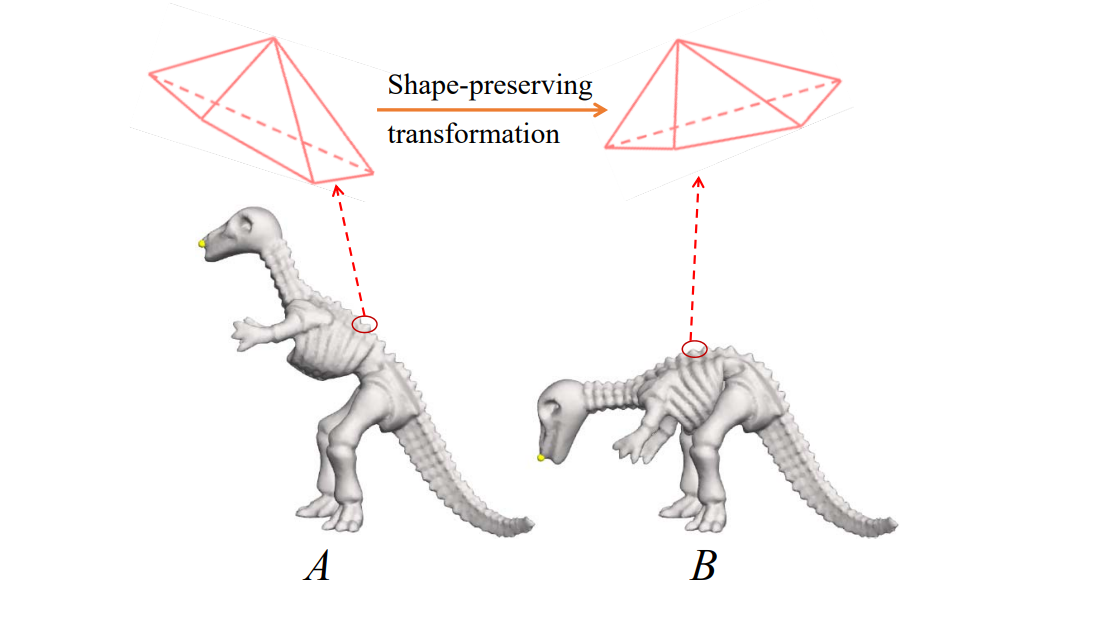
Mesh transplanting

• The user defines
  • Part to transplant
  • Where to transplant
  • Spatial orientation and scale
• Topological stitching
• Geometrical stitching via Laplacian mixing

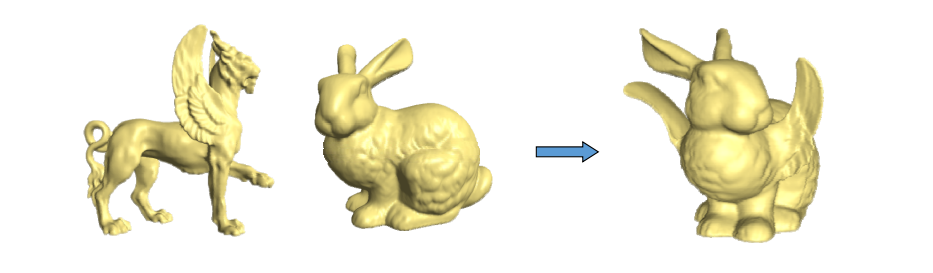
• Details gradually change in the transition area

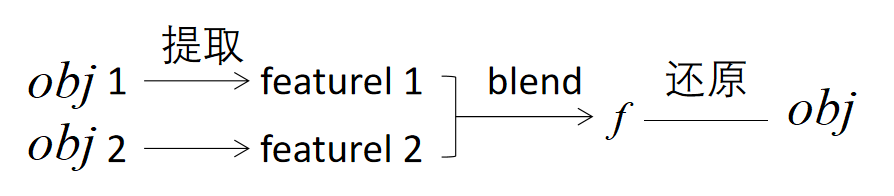
提取与还原即 Encoder& Decoder.Laplace 是手工方法，E&D是AI方法。

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/