为什么引入B样条曲线

Bezier曲线的不足

$$ x(t)=\sum_{i=0}^{n} B_i^n(t)\cdot b_i $$

每个基函数在整平[0，1]作用域上都有值，因此具有全局性。 任意一个点的移动都会影响整条曲线。
全局性：牵一发而动全身，不利于设计

❓ 不是可以通过分段来解决吗？
答：可以，但要分成多个函数来表达。B样条用统一的函数表达分段曲线。

样条曲线的不足

分段的多项式曲线（Bezier曲线）
优点：分段表达，具有局部性
缺点：要分成多个函数来表达。

思考：以统一的方式表达分段函数

基函数应满足的性质

形式类比：每个控制顶点用一个基函数进行组合

$$ x(t)=\sum_{i=0}^{n} N_{i,k}(t)\cdot d_i $$

其中\(d_i\)为控制顶点，\(N\)为基函数。

基函数性质要求：
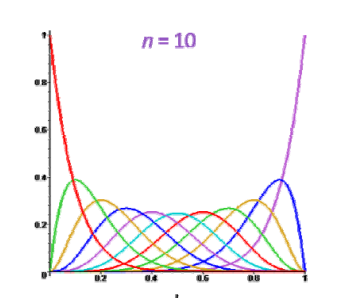
• 基函数须局部性（局部支集）
• 基函数要有正性+权性

启发：

【Bernstein基函数的递推公式】：link

思路：

• 局部处处类似定义，由一个基函数平移得到
• 高阶的基函数由2个低阶的基函数“升阶”得到，利于保持一些良好的性质，比如提高光滑性

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/