B‐spline curves 的定义

Given:
$𝑛+1$ control points $𝒅_0,\dots,d_n∈\mathbb{R} ^3$
参数化向量 $𝑇=(t_0,\dots,t_n,\dots,t_{n+k})$

$𝒅_i$ 又称为 de Boor points

Then：
k阶 B‐spline curve 𝒙(𝑡) 定义为：

$$ x(t)=\sum_{i=0}^{n} N_{i,k}(t)\cdot d_i $$

B样条本质是分段曲线、但通过 local basis funchion 的方法，有一个公式统一了所有分段曲线。

B‐spline curves 的例子

$k=4,n=5$

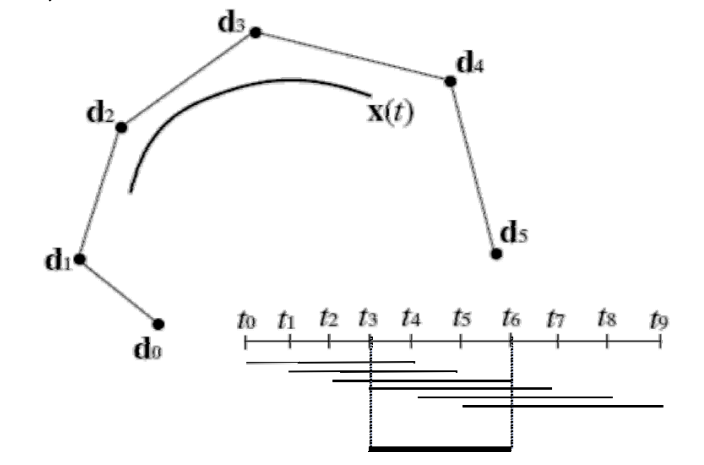
Support intervals of $𝑁_{i,k}$

由于$n=5$，$d_0-d_5$定义第一条曲线，$d_1-d_6$定义第二条曲线。
本质上是分段曲线，在连接点上C3连续。

Multiple weighted knot vectors

例子中的$𝑇=(t_0,\dots,t_n,\dots,t_{n+k})$ 满足 $t_0< t_1< \dots< t_{n+k}$
但也可以定义为$t_0\le t_1\le \dots\le t_{n+k}$，即结点重合。

结点重合会导致连续性下降，每增加一重、连续性减一。可以以此方法控制曲线的连续性。
可以根据重合度控制结点的光滑性。
• The recursive definition of the B spline function $𝑁_{i,k}(i=0,\dots,n) $ works nonetheless as long as no more than 𝑘 knots coincide

首未端点插值

set: $t_0=t_1=\dots=t_{k-1}$ and $t_{n+1}=t_{n+2}=\dots=t_{n+k}$

$𝒅_0$ and $𝒅_n$ are interpolated

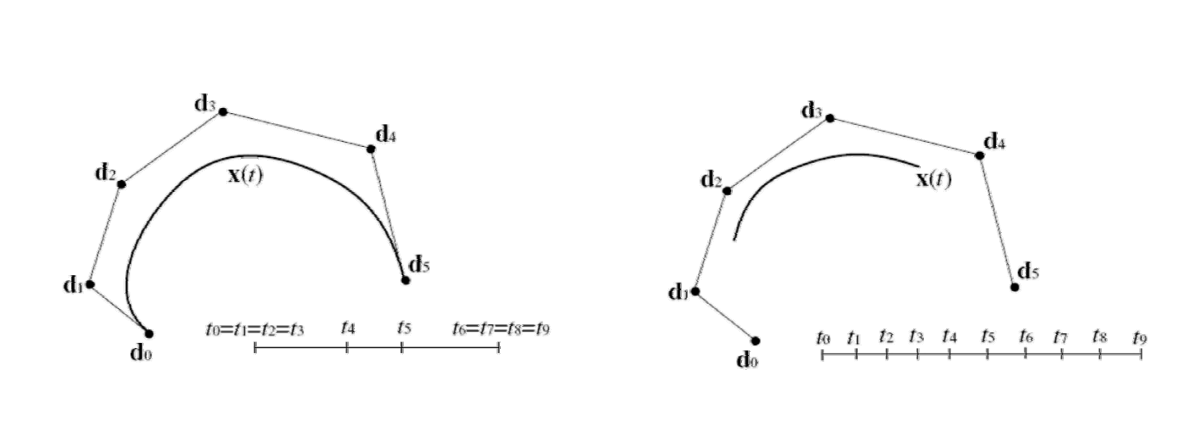
要使首未端点被插值，需要把首未端点设置为$K$重。把B-spline curve 的两个端点都设成$n-1$重，就会退化为 Bezier curve.

B‐spline curves的性质

性质1：退化

要使首未端点被插值，需要把首未端点设置为$K$重。把B-spline curve 的两个端点都设成$n-1$重，就会退化为 Bezier curve.

性质2：连续性

结点重合会reduction of continuity of$𝑥(𝑡)$。𝑙重结点 $(1\le 𝑙 < 𝑘)$ means $𝐶^{k-𝑙-1}$ continuity

性质3：局部性

moving of $𝑑_i$ only changes the curve in the region $[𝑡_i,t_{i+k}]$
The insertion of new de Boor points does not change the polynomial degree of the curve segments

[1:10:41] 💡 在神经网络中把 acfivation 改为 local basis funchion. 这样，只需更新 N N 的部分参数。

B样条的计算 The de Boor algorithm

算法背景

输入：
de Boor points：$𝒅_0,…,𝒅_n$

Knot vector：

$$ (t_0,\cdots ,t_{k-1}=t_0,t_k,t_{k+1},\dots ,t_n,t_{n+1},\dots ,t_{n+k}=t_{n+1}) $$

输出：
Curve point $𝒙(𝑡)$ of the k 阶B‐spline curve

算法过程

不断地插入结点就可以得到B样条曲线

Search index with $t_r\le t\le t_{r+1}$

for i=r-k+1,... ,r
    d^0_i=d_i
for j=1, ... ,k-1   
    for i=r-k+1+j,\cdots ,r    
        a_i^j={t-t_i}/{t_{i+k-j}-t_i}
        d_i^j=(1-a^j_i) \cdot  d^{j-1}_{i-1}+a_j^i \cdot  d^{j-1}_i
d^{k-1}_r=x(t)

B样条的其他理论知识

B样条的许多性质
• 局部凸包性、变差缩减性、包络性
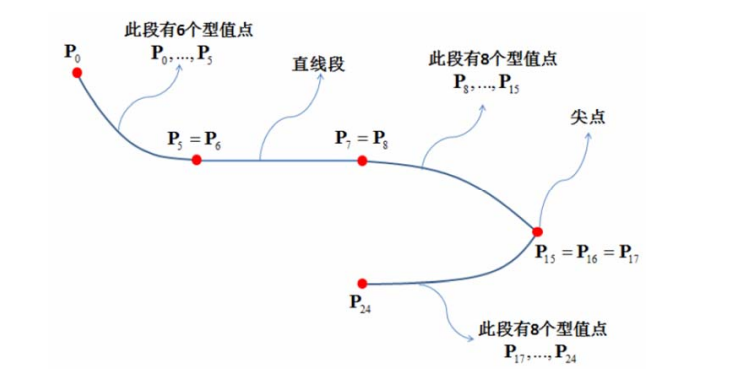
• B样条的导数、积分递推式、几何作图
重节点的B样条基函数及B样条曲线
Bezier样条曲线转换为B样条曲线
B样条插值方法
…

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/